在完成了分配任务之后，西部 314 来到了楼兰古城的西部。

相传很久以前这片土地上(比楼兰古城还早)生活着两个部落，一个部落崇拜尖刀(V)，一个部落崇拜铁锹(∧)，他们分别用 V 和 ∧ 的形状来代表各自部落的图腾。

西部 314 在楼兰古城的下面发现了一幅巨大的壁画，壁画上被标记出了 n 个点，经测量发现这 n 个点的水平位置和竖直位置是两两不同的。

西部 314 认为这幅壁画所包含的信息与这 n 个点的相对位置有关，因此不妨设坐标分别为 (1,y1),(2,y2),…,(n,yn)，其中 y1∼yn 是 1 到 n 的一个排列。

西部 314 打算研究这幅壁画中包含着多少个图腾。

如果三个点 (i,yi),(j,yj),(k,yk) 满足 1≤i<j<k≤n 且 yi>yj,yj<yk，则称这三个点构成 V 图腾;

如果三个点 (i,yi),(j,yj),(k,yk) 满足 1≤i<j<k≤n 且 yi<yj,yj>yk，则称这三个点构成 ∧ 图腾;

西部 314 想知道，这 n 个点中两个部落图腾的数目。

因此，你需要编写一个程序来求出 V 的个数和 ∧ 的个数。

输入格式
第一行一个数 n。

第二行是 n 个数，分别代表 y1，y2,…,yn。

输出格式
两个数，中间用空格隔开，依次为 V 的个数和 ∧ 的个数。

数据范围
对于所有数据，n≤200000，且输出答案不会超过 int64。
y1∼yn 是 1 到 n 的一个排列。

输入样例：
5
1 5 3 2 4
输出样例：
3 4

分析

1. 当我们需要实现单点修改、区间查询，如果用普通的前缀和的话，查询O(1)，修改后的话需要重新计算前缀和，那就又O(n)了，如果m次查询，那就O(m*n)的复杂度了，特殊情况肯定TLE；所以我们引入一种新的数据结构，就是树状数组，他的单点修改、区间查询都是O(logn)的复杂度；
2. 要学树状数组，一共三个函数，首先了解一个lowbit函数，他是求x的二进制序列中最低位的1加上其后面所有0所对应的十进制的值；比如：lowbit(8)=lowbit([1000])=2^3=8；可以使用x & -x来计算；
3. add(x,c)函数就是将序列中第x个数(a[i])加上c，i从x开始，i 每次+=lowbit(i)，然后向上更新，tr[i] += c；（改了一个点a[i]，影响的是唯一的父节点，是一个单链路径，tr[i]结点的父结点为t[i + lowbit(x)]）
4. sum(x)函数是1到x位置的区间和，在这题sum就是查询x之前( 区间[1,x] )的元素出现次数之和，注意此题是查的次数，树状数组存的是出现次数的前缀和；
5. 树状数组tr的含义：tr[N]相当于c[N]，tr[i] =【i,lowbit(i)】，表示以i结尾，长度为lowbit(i)的区间和，这里是出现次数的前缀和;
6. 然后这个题，先从左到右，V的个数就是，i从1到n枚举y=a[i]，看看其左边有多少个数小于他，保存在low中；看看其左边有多少个数大于他，保存在gre中，然后把当前的y加入树状数组；最后计算完从左到右，然后清空树状数组，计算从右到左，(sum(n) - sum(y))就相当于从右到左的gre[i]；那么当前yj=y时的V的方案数就是：左边比他大的个数 乘 右边比他大的个数；同样 ∧型也如此；
7. 下面所有图片来源于acwing的一位大佬：AcWing 241. 楼兰图腾 作者： qiaoxinwei ；可以比较容易的理解add、sum操作的过程；而且链接里面有暴力O(n*n)的解法，思路也是很不错的，维护4个前缀数组，可以去参考；

此题解题思路：

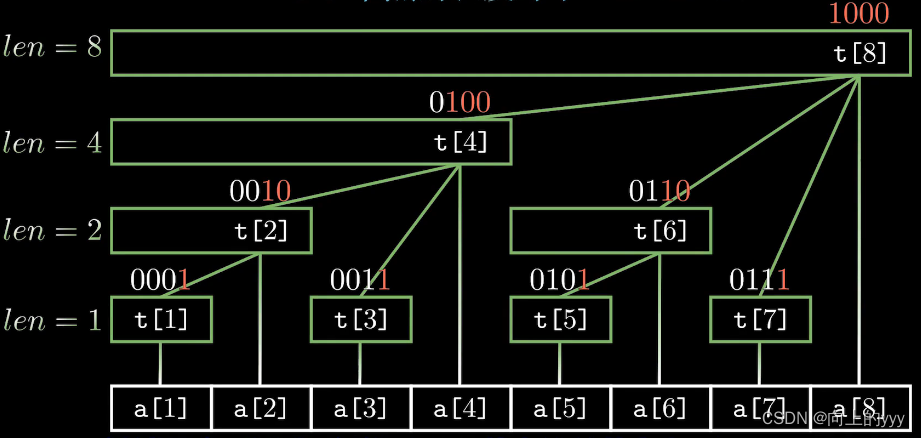
一个序列的树形结构：

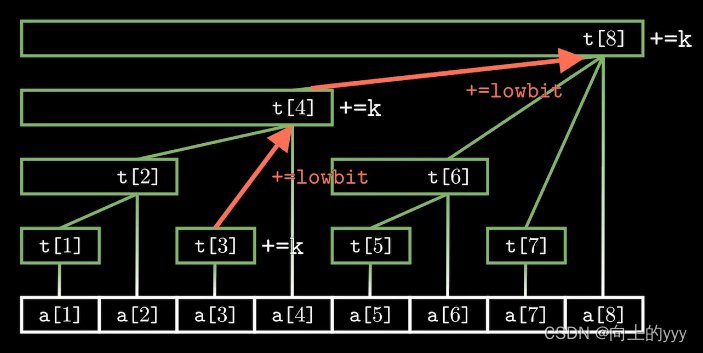
add(x,k)表示将序列中第x个数加上k，在整棵树上维护这个值，需要一层一层向上找到父结点，并将这些结点上的tr[x]值都加上k

sum(x)：表示将查询序列前x个数的和

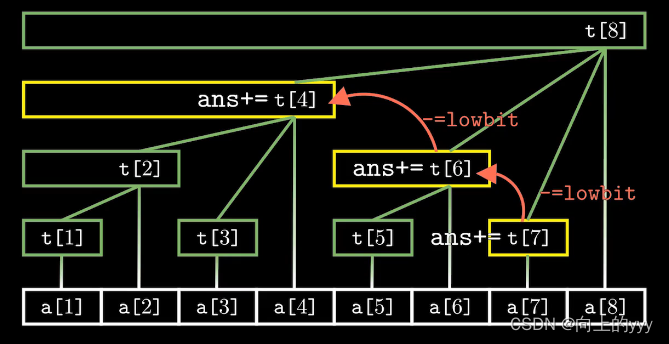
查询sum(7)的前缀和，需要从这个点向左上找到上一个结点，将加上其结点的值tr[i]。向左上找到上一个结点，只需要将下标 x -= lowbit(x)，例如 7 - lowbit(7) = 6，6-lowbit(6)=4，不断向左上找；

#include <bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 200010;
int n;
int a[N];
int tr[N];//树状数组,相当于c，tr[i] =【i,lowbit(i)】，表示以i结尾，长度为lowbit(i)的区间和，这里是出现次数的前缀和
int low[N];//low[i]：i位置前面 小于a[i]的个数
int gre[N];//gre[i]：i位置前面 大于a[i]的个数

//求x的二进制序列中最低位的1所对应的值
int lowbit(int x) {
    return x & -x;
}

//自下而上更新,将序列中第x个数加上c,此题的c表示次数
void add(int x, int c) {
    for (int i = x; i <= n; i += lowbit(i))
        tr[i] += c;
}

//查询值为x的位置之前([1,x])的元素出现 次数 之和
LL sum(int x) {
    LL res = 0;
    for (int i = x; i; i -= lowbit(i))
        res += tr[i];
    return res;
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
    }
    //1. 从左向右统计比 a[i] 小的个数、大的个数
    for (int i = 1; i <= n; ++i) {
        int y = a[i];
        //已加入树状数组的数中，值为 y+1~n 有多少个数（比a[i]大的个数）
        gre[i] = sum(n) - sum(y);
        //已加入树状数组的数中，值为 1~y-1 有多少个数（比a[i]小的个数）
        low[i] = sum(y - 1);
        //将y加入树状数组，y出现一次
        add(y, 1);
    }
    //2. 从右向左统计比a[i]小的个数、大的个数
    LL ansA = 0, ansV = 0;//呈V、A型的个数
    memset(tr, 0, sizeof tr);
    for (int i = n; i > 0; --i) {
        int y = a[i];
        ansV += gre[i] * (sum(n) - sum(y));//a[i]左边大于a[i]个数 * 右边大于a[i]个数
        ansA += low[i] * sum(y - 1); //a[i]左边小于a[i]个数 * 右边小于a[i]个数
        //将y加入树状数组
        add(y, 1);
    }
    cout << ansV << " " << ansA;
    return 0;
}