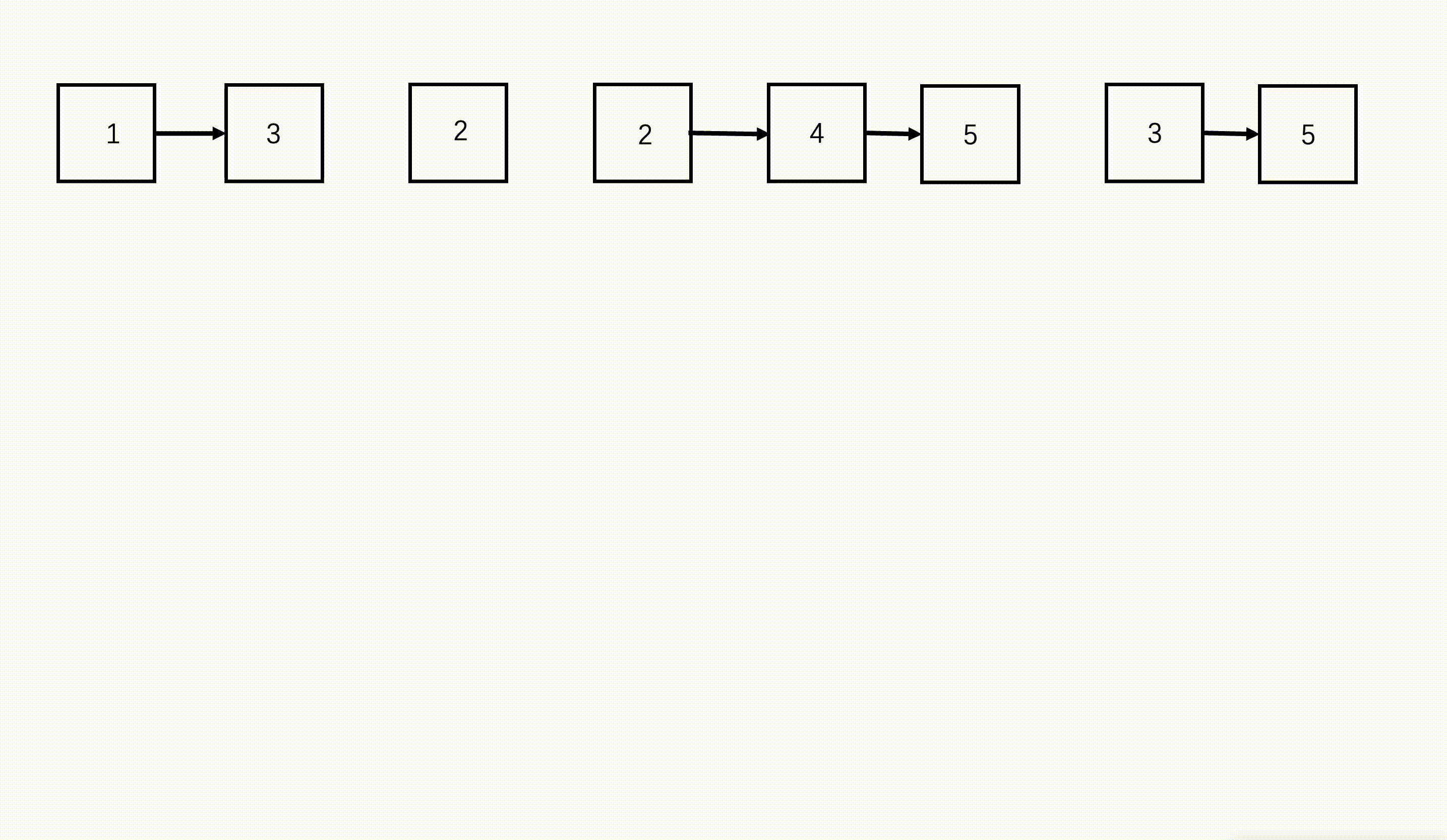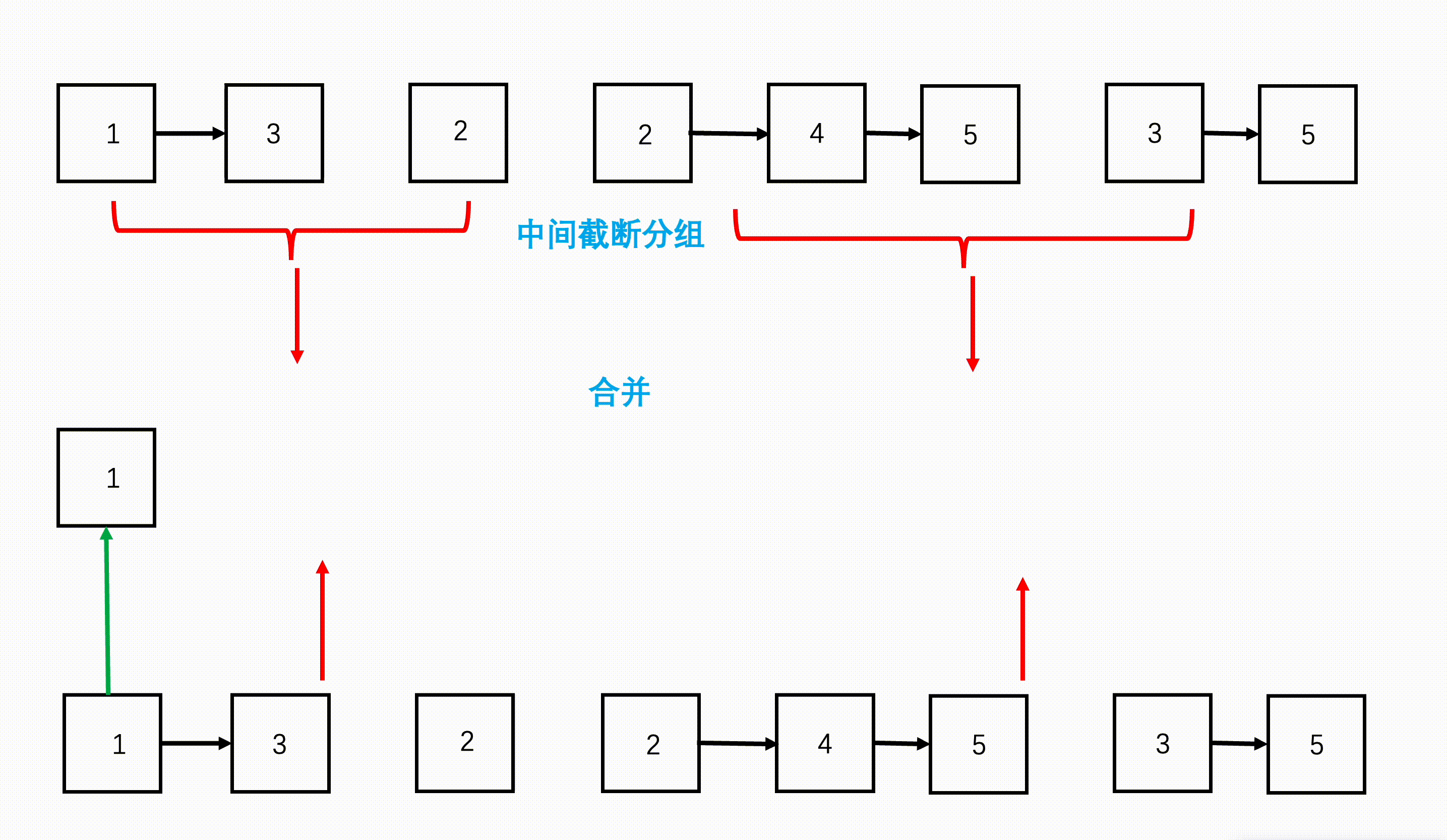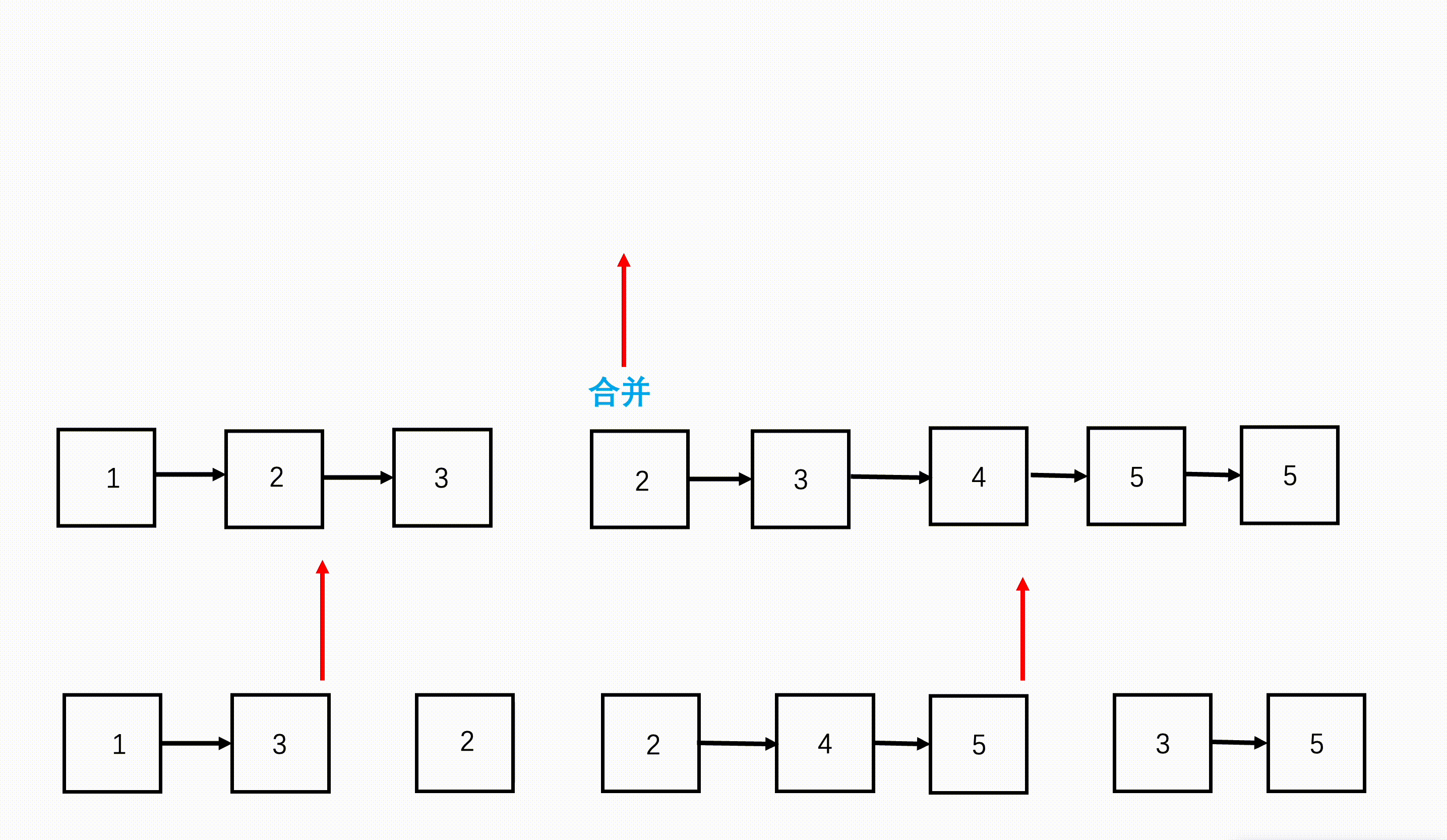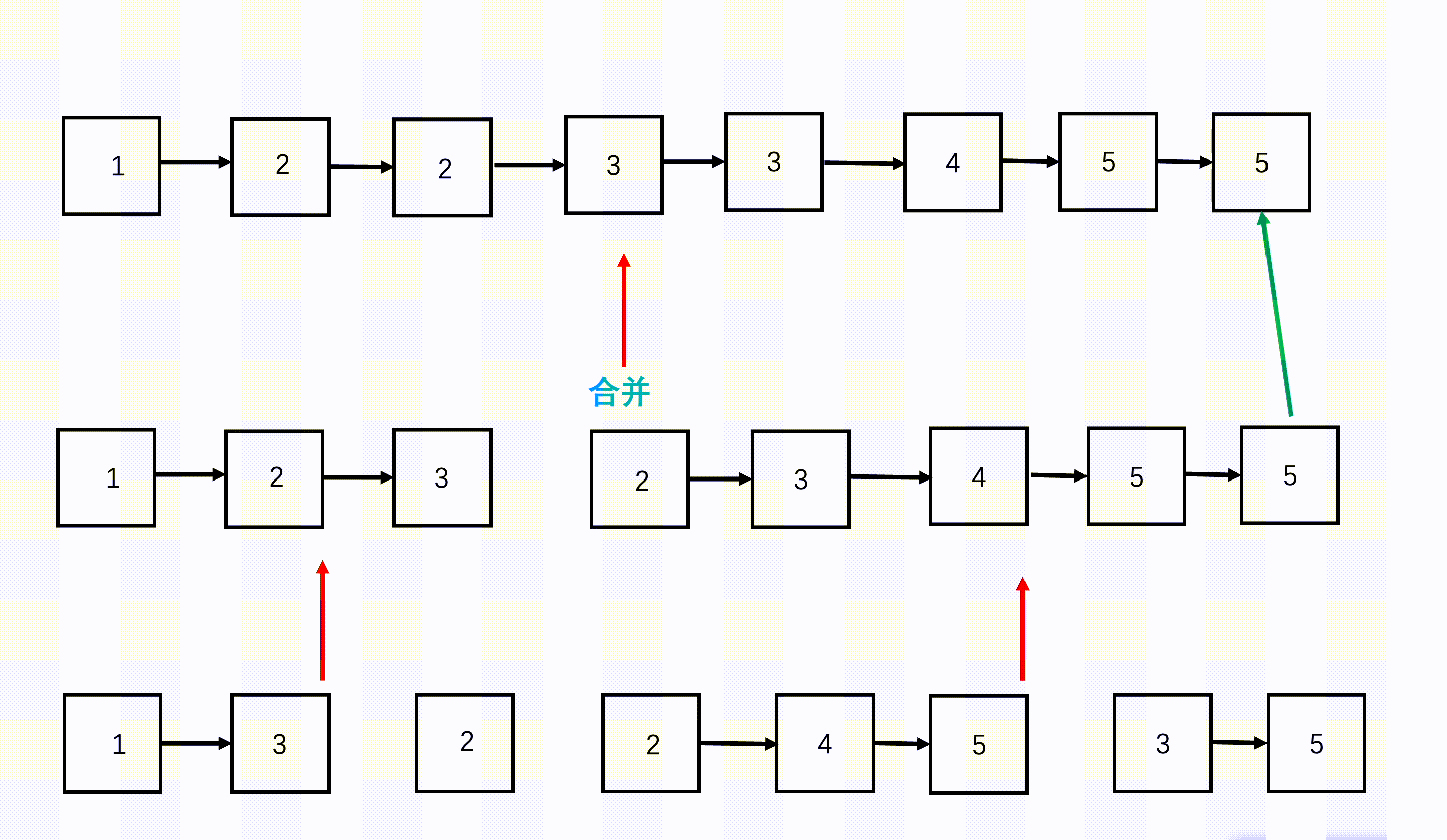食用指南:本文为作者刷题中认为有必要记录的题目
♈️今日夜电波:保留—郭顶
1:33 ━━━━━━️💟──────── 4:30
🔄 ◀️ ⏸ ▶️ ☰
💗关注👍点赞🙌收藏您的每一次鼓励都是对我莫大的支持😍
目录
什么是回溯法?
回溯法用在何处?
回溯法的理解
🌸一、组合
💮二、组合总和
🌺三、组合总和II
什么是回溯法?
回溯法的实现方式是通过递归函数来实现的,每次递归时都会考虑一种可能的解,并判断这种解是否符合要求。如果符合要求,就返回这个解;如果不符合要求,就回溯到上一步,尝试另一种可能的解。回溯算法常用于求解组合、排列、子集等问题,例如八皇后问题、数独等。回溯算法的时间复杂度通常比较高,因为需要枚举所有可能的解,所以在实际应用中需要考虑优化算法。
回溯法用在何处?
回溯法通常用于解决以下问题:
1. 生成所有的排列或组合。
2. 解决搜索问题,如迷宫问题、数独问题、八皇后问题等。
3. 解决决策问题,如0-1背包问题、旅行商问题等。
4. 解决图论问题,如最小生成树问题、哈密尔顿回路问题等。
在这些问题中,回溯法一般通过深度优先搜索的方式遍历所有的可能性,直到找到符合条件的解或搜索到所有可能性。
回溯法的理解
本文参考了一位大佬的题解,详细的介绍了回溯法:链接
记住一句话:for循环横向遍历,递归纵向遍历,回溯不断调整结果集。 这句话将从始至终贯穿我们对于以上问题的回溯解决办法。
🌸一、组合
题目链接:77. 组合
题目描述:
给定两个整数
n和k,返回范围[1, n]中所有可能的k个数的组合。你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]
示例 2:
输入:n = 1, k = 1 输出:[[1]]
提示:
1 <= n <= 201 <= k <= n
本题思路:
采用经典的“回溯三部曲”:
1、定义两个全局变量,一个用来存放符合条件单一结果(path),一个用来存放符合条件结果的集合(result)。注意要记得用一个变量来记录遍历的位置。
2、回溯的主体,回溯终止条件。path保存一组数据,每次遍历到叶子节点,再插入到result中,并且回溯到上一个节点。
3、单层搜索的过程。for循环用来横向遍历,递归的过程是纵向遍历。
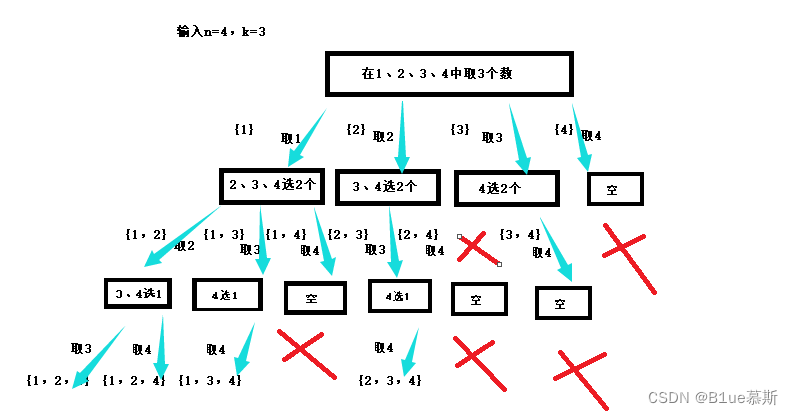
一图流:(以n=4,k=3为例)
class Solution {
public:
vector<vector<int>> rtu;
vector<int> path;
void backtrack(int n,int k,int index)
{
if(path.size()==k)//结束条件
{
rtu.push_back(path);
return;
}
for(int i=index;i<=n;i++)//横向遍历
{
path.push_back(i);
backtrack(n,k,i+1);//纵向递归
path.pop_back();//回溯
}
}
public:
vector<vector<int>> combine(int n, int k) {
backtrack(n,k,1);
return rtu;
}
};加入剪枝优化:
class Solution {
public:
vector<vector<int>> rtu;
vector<int> path;
void backtrack(int n,int k,int index)
{
if(path.size()==k)//结束条件
{
rtu.push_back(path);
return;
}
for(int i=index;i<=n-(k-path.size())+1;i++)//横向遍历
{
path.push_back(i);
backtrack(n,k,i+1);//纵向递归
path.pop_back();//回溯
}
}
public:
vector<vector<int>> combine(int n, int k) {
backtrack(n,k,1);
return rtu;
}
};
💮二、组合总和
题目链接:39. 组合总和
题目描述:
给你一个 无重复元素 的整数数组
candidates和一个目标整数target,找出candidates中可以使数字和为目标数target的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。对于给定的输入,保证和为
target的不同组合数少于150个。
示例 1:
输入:candidates = [2,3,6,7], target = 7 输出:[[2,2,3],[7]] 解释: 2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。 7 也是一个候选, 7 = 7 。 仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8 输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1 输出: [] 提示:
1 <= candidates.length <= 302 <= candidates[i] <= 40candidates的所有元素 互不相同1 <= target <= 40
本题思路:
同样采用经典的“回溯三部曲”,但是做了些许改变。相较于上一题,在这里不需要对于index进行+1操作,跳出循环条件改为对target的两次判断。增加一个变量用于记录总和。
class Solution {
public:
vector<int> path;
vector<vector<int>> rtu;
void backtrack(vector<int>& candidates,int target,int index,int sum)
{
if(target==sum)
{
rtu.push_back(path);
return;
}
if(sum>target)
{
return;
}
for(int i=index;i<candidates.size();i++)
{
sum+=candidates[i];
path.push_back(candidates[i]);
backtrack(candidates,target,i,sum);
path.pop_back();
sum-=candidates[i];
}
}
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
rtu.clear();
path.clear();
backtrack(candidates,target,0,0);
return rtu;
}
};
加入剪枝优化:
class Solution {
public:
vector<int> path;
vector<vector<int>> rtu;
void backtrack(vector<int>& candidates,int target,int index,int sum)
{
if(target==sum)
{
rtu.push_back(path);
return;
}
if(sum>target)
{
return;
}
for(int i=index;i<candidates.size()&&sum + candidates[i] <= target;i++)
{
sum+=candidates[i];
path.push_back(candidates[i]);
backtrack(candidates,target,i,sum);
path.pop_back();
sum-=candidates[i];
}
}
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
rtu.clear();
path.clear();
sort(candidates.begin(),candidates.end());
backtrack(candidates,target,0,0);
return rtu;
}
};
🌺三、组合总和II
题目链接:40. 组合总和 II
题目描述:
给定一个候选人编号的集合
candidates和一个目标数target,找出candidates中所有可以使数字和为target的组合。
candidates中的每个数字在每个组合中只能使用 一次 。注意:解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5 输出: [ [1,2,2], [5] ]
提示:
1 <= candidates.length <= 1001 <= candidates[i] <= 501 <= target <= 30
本题思路:
这里相较于上一题主要的变动为去重的操作:
如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false,就说明:前一个树枝,使用了candidates[i - 1],也就是说同一树层使用过candidates[i - 1]。基于以上再加入剪枝操作就可以完成去重的操作了!与此相对的还要对for循环加入continue操作。
class Solution {
public:
vector<int> path;
vector<vector<int>> rtu;
void backtrack(vector<int>& candidates, int target,int num,int index,vector<bool>& used)
{
if(target==num)
{
rtu.push_back(path);
return;
}
for(int i=index;i<candidates.size()&&num+candidates[i]<=target;i++)
{
if(i>0&&candidates[i]==candidates[i-1]&&used[i-1]==false)
continue;
num+=candidates[i];
path.push_back(candidates[i]);
used[i]=1;
backtrack(candidates,target,num,i+1,used);
num-=candidates[i];
path.pop_back();
used[i]=0;
}
}
public:
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
vector<bool> used(candidates.size(), false);
path.clear();
rtu.clear();
sort(candidates.begin(),candidates.end());
backtrack(candidates,target,0,0,used);
return rtu;
}
};
感谢你耐心的看到这里ღ( ´・ᴗ・` )比心,如有哪里有错误请踢一脚作者o(╥﹏╥)o!

给个三连再走嘛~