文章目录
- 安装前准备
- 创建挂载目录
- 授权相关权限
- 创建elasticsearch.yml文件
- 拉取镜像
- 运行容器
- 查看运行情况
- 测试
安装前准备
创建挂载目录
用于在宿主机挂载日志,数据等内容
创建/opt/es/data目录
创建/opt/es/logs目录
创建/opt/es/plugins目录
创建/opt/es/conf目录
mkdir -p /opt/es/{data,logs,plugins,conf}
授权相关权限
chmod -R 777 /opt/es/data
chmod -R 777 /opt/es/logs
chmod -R 777 /opt/es/conf
chmod -R 777 /opt/es/plugins
创建elasticsearch.yml文件
vim /opt/es/conf/elasticsearch.yml
内容

http.host: 0.0.0.0
拉取镜像
docker pull elasticsearch:7.17.2
运行容器
docker run --name elasticsearch -p 9200:9200 -p 9300:9300 \
-e "discovery.type=single-node" \
-e ES_JAVA_OPTS="-Xms84m -Xmx512m" \
-v /opt/es/conf/elasticsearch.yml:/usr/share/elasticsearch/config/elasticsearch.yml \
-v /opt/es/data:/usr/share/elasticsearch/data \
-v /opt/es/plugins:/usr/share/elasticsearch/plugins \
-d elasticsearch:7.17.2

查看运行情况

运行成功
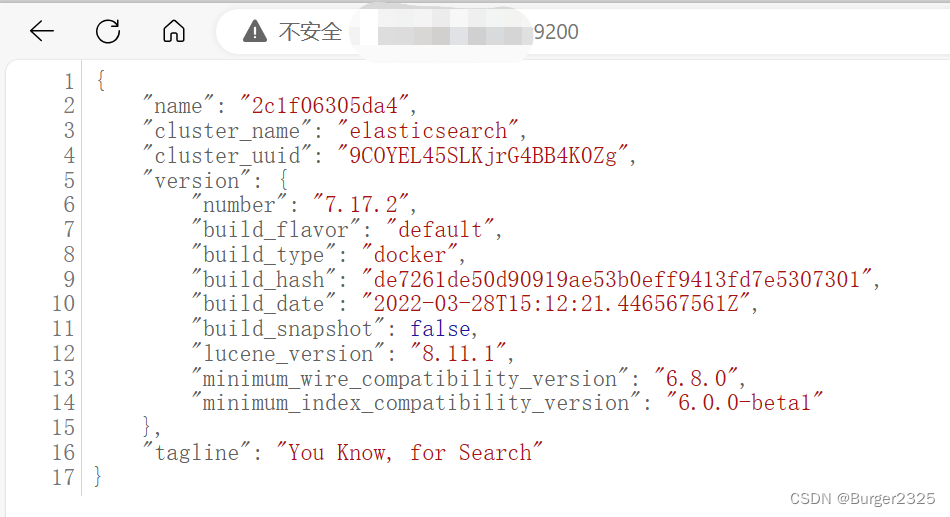
测试
URL:IP:9200
出现以下画面即可