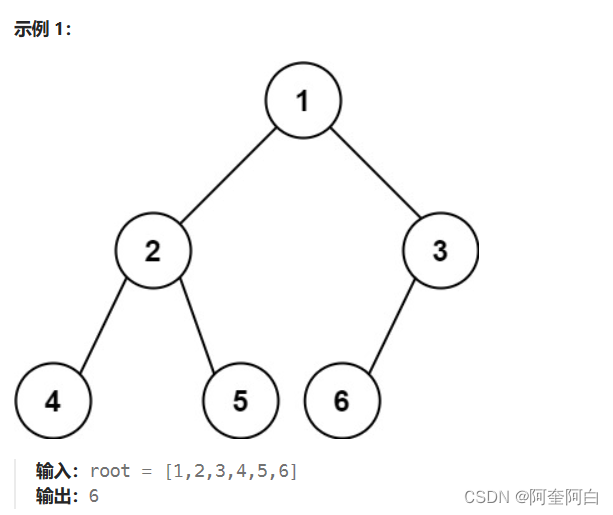
给出一个完全二叉树，求出该树的节点个数。

——————————————————————————————————————

1. 普通二叉树的求法

递归法与求深度类似，但是深度是depth++,而此题是计算nodeNum。

迭代法使用层序遍历，记录遍历的节点个数即可。

递归法

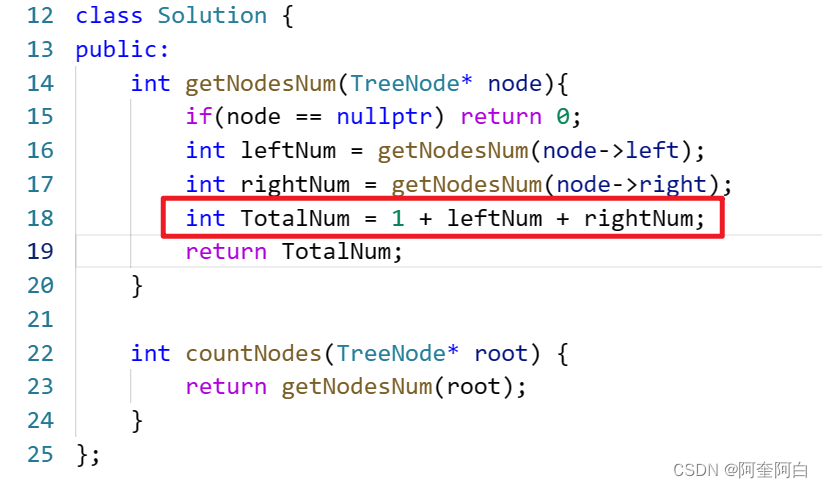
迭代法

层序遍历的模板是通用的，不一定只适用完全二叉树。

2. 完全二叉树的求法

完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。

对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。

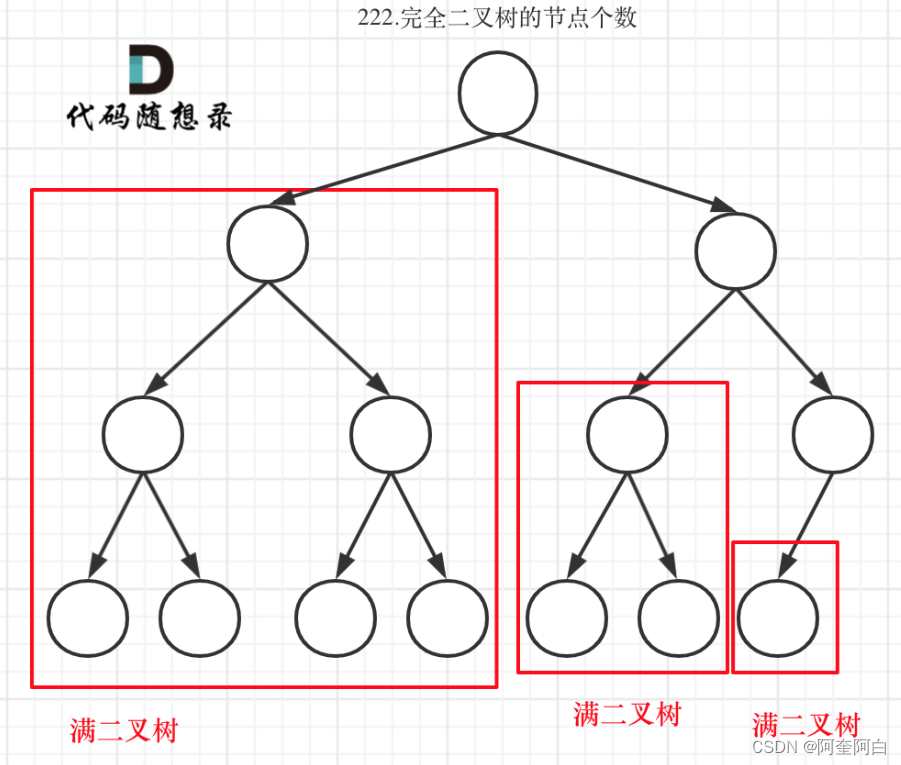
可以看出如果整个树不是满二叉树，就递归其左右孩子，直到遇到满二叉树为止，用公式计算这个子树（满二叉树）的节点数量。

这里关键在于如何去判断一个左子树或者右子树是不是满二叉树呢？

在完全二叉树中，如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树。如图：

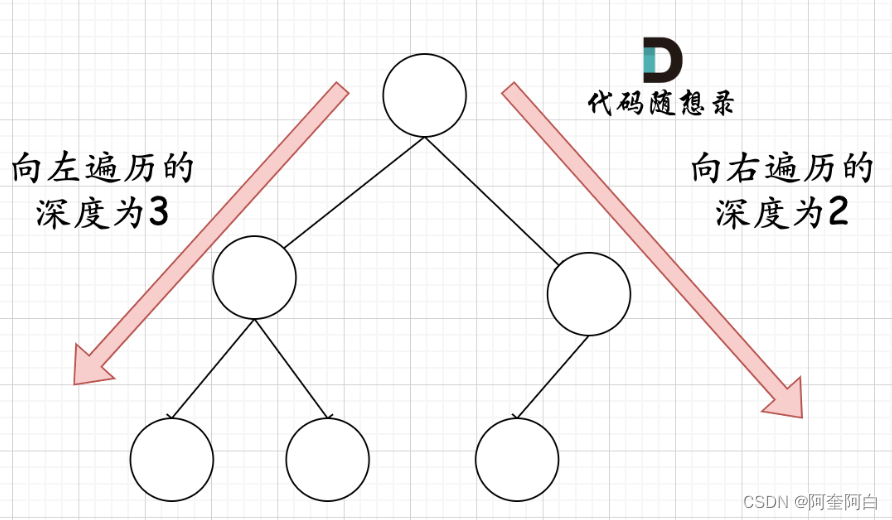
在递归逻辑中，第二步的终止条件为：判断左右子树的深度是否相等来判断是否为满二叉树。

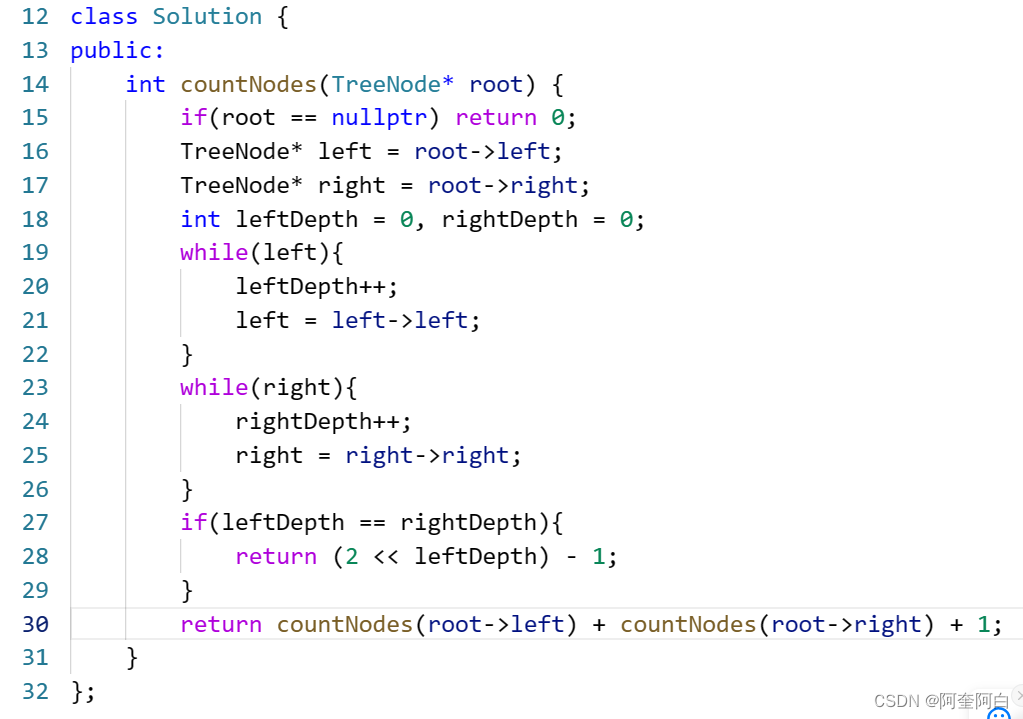
if (root == nullptr) return 0; 
// 开始根据左深度和右深度是否相同来判断该子树是不是满二叉树
TreeNode* left = root->left;
TreeNode* right = root->right;
int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的，为了下面求指数方便
while (left) {  // 求左子树深度
    left = left->left;
    leftDepth++;
}
while (right) { // 求右子树深度
    right = right->right;
    rightDepth++;
}
if (leftDepth == rightDepth) {
    return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2，返回满足满二叉树的子树节点数量
}

单层递归的逻辑则是后序遍历，求节点数。

return countNodes(root->left) + countNodes(root->right) + 1; 

整体的迭代法：