【GRU回归预测】基于matlab鲸鱼算法优化门控循环单元WOA-GRU神经网络回归预测（多输入单输出）【含Matlab源码 2285期】

news2024/11/17 8:23:22

⛄一、CNN-GRU数据预测

1 理论基础
1.1 CNN算法
负荷序列数据为一维数据，用一维卷积核对数据进行卷积处理，以获取数据的特征。
现设定卷积核的维度为3，移动步长为1，对输入数据进行卷积，以获得特征图图谱，即：
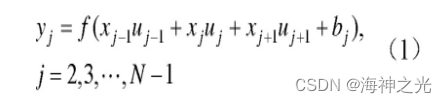
在这里插入图片描述
式中：yj为第j个位置的特征值输出；xj为第j个位置的数据值；uj为第j个位置的卷积核值。

1.2 GRU算法
将经过卷积之后产生的特征序列作为GRU的输入。GRU由LSTM发展而来，LSTM是RNN的变体。RNN网络通过对输入信号的循环保证了信号的持续存在。LSTM是由RNN网络改进而来，在RNN的基础上加入了记忆单元和门机制，有效地解决了长序列训练中存在的梯度消失和梯度爆炸问题。

LSTM用输入门、遗忘门和输出门3个门函数来控制输入值、遗忘值和输出值。GRU网络较LSTM网络有所简化，GRU网络由新门和重置门两个门函数构成，其结构如图1所示。
在这里插入图片描述
图1 GRU的网络结构图
zt为更新门，用来决定上一层隐藏层状态中有多少信息传递到当前的隐藏状态ht中，经过sigmoid函数将结果映射到0～1之间，即：

rt为重置门，决定上一时刻隐藏层状态有多少信息需要被遗忘，经过sigmoid函数将结果映射到0～1之间，越接近1信息越容易被保留，即：
在这里插入图片描述
确定当前的记忆内容，将重置门rt与ht–1进行Hadamard乘积决定当前的记忆内容中要遗忘多少上一时刻的隐藏层的内容，然后与新的输入数据结合放入tanh激活函数中，即：

最后确定当前隐藏层保留的信息，通过zt和1–zt确定哪些历史数据和当前数据需要更新，即：
在这里插入图片描述
2 鲸鱼群算法优化门控循环神经网络（GRU-WOA）
首先初始化训练数据。设置鲸鱼群种群数量为 100，目标函数初始化设为 1e10，设定最大迭代次数为 100。鲸鱼群算法优化循环神经网络的连接权值，鲸群中个体的位置向量与网络迭代过程中的权值及阈值对应。样本训练产生的均方差为鲸鱼的适应度函数。利用鲸群 3 个公式
更新位置，并将其代替梯度下降法训练循环神经网络。不断迭代训练，直到期望误差或迭代次数达标。鲸鱼群算法优化循环神经网络步骤如下：
（1）初始化网络模型。包括隐藏层个数、最大迭代次数等。
（2）设置循环神经网络权重个数和鲸鱼个数，二者相等。
（3）计算鲸鱼适应度值，进行排序，找出全局最优。本文将均方差误差作为适应度函数。
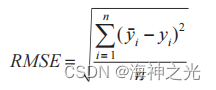
在这里插入图片描述
其中，yˉi 表示预测值，yi 表示真实值，n 表示样本个数。
（4）按照式（13）更新鲸鱼个体位置，迭代数加一。
（5）判断算法是否满足终止要求，若没有则进行第（3）步，否则进行第（6）步。
（6）对鲸鱼位置向量赋予网络权值。
（7）采用梯度下降算法进行模型训练，当迭代次数到达规定次数，若损失函数收敛，则训练完成；若未收敛，则继续迭代直至收敛。
（8）输入训练样本数据，输出预测值。

⛄二、部分源代码

% 清空环境变量
warning off % 关闭报警信息
clear all % 清空变量
clc % 清空命令行
% close all % 关闭开启的图窗

%% 导入数据
% 训练集——190个样本
P_train = xlsread(‘data1’,‘training set’,‘B2：G191’)‘; T_train= xlsread(‘data1’,‘training set’,‘H2：H191’)’;
% 测试集——44个样本
P_test=xlsread(‘data1’,‘test set’,‘B2:G45’)‘;T_test=xlsread(‘data1’,‘test set’,‘H2:H45’)’;
shuru_num = size(P_train ,1); % 输入维度
shuchu_num=1;
N = size(P_test, 2); % 测试集样本数
M = size(P_train, 2); % 训练集样本数

%% 数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax(‘apply’, P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax(‘apply’, T_test, ps_output);

%% 优化算法
pop = 20; %种群数量
Max_iter = 20; %最大迭代次数
lb = [10 0.001] ; %下边界
ub = [200 0.015]; %上边界
dim = 2; %维度
fobj=@(X)fobj(X,p_train,t_train,p_test,t_test,shuru_num,shuchu_num );
[ Best_score, Best_P,curve] = WOA(pop, Max_iter, lb, ub, dim, fobj);

%% 重新训练
disp([‘最佳光滑因子值为’,num2str(Best_P)])
Best_P(1)=round(Best_P(1));
layers = [ …
sequenceInputLayer(shuru_num)
gruLayer(Best_P(1))
fullyConnectedLayer(shuchu_num)
regressionLayer];
options = trainingOptions(‘adam’, … % 梯度下降
‘MaxEpochs’,50, … % 最大迭代次数
‘GradientThreshold’,1, … % 梯度阈值
‘InitialLearnRate’,Best_P(2));
net = trainNetwork(p_train,t_train,layers,options);
%% 预测