Empowering Long-tail Item Recommendation through Cross Decoupling Network (CDN)
来源:
- KDD’2023
- Google Research
文章目录
- Empowering Long-tail Item Recommendation through Cross Decoupling Network (CDN)
- 长尾问题分析
- CDN
- Item Memorization and Generalization Decoupling
- 记忆特征(Memorization features)
- 泛化特征(Generalization features)
- 物品表征学习
- User Sample Decoupling
- Cross Learning
- 总结
- 参考
长尾问题是个老大难问题了。
在推荐中可以是用户/物料冷启动,在搜索中可以是中低频query、文档,在分类问题中可以是类别不均衡。长尾数据就像机器学习领域的一朵乌云,飘到哪哪里就阴暗一片。今天就介绍来自Google的一篇解决长尾物品推荐的论文。
真实推荐场景下,大部分物品都是长尾物品,即小部分物品占据了绝大部分的交互,大部分物品的交互次数很少。人们一直都致力解决这个问题,但往往不能在真实环境下部署,要么对整体的效果大打折扣。在这篇论文里,作者致力于维持整体效果、保成本的条件下提高长尾物品的推荐效果(是否需要专门评估在长尾物品上的推荐效果?)。为了达到这个目标,作者设计了Cross Decoupling Network (CDN)。
CDN借鉴了计算机视觉里的一个想法1(借鉴的这篇论文也是研究长尾问题的,感觉值得阅读一下),该方法的核心思想是两阶段的学习策略:第一阶段在长尾分布的数据集上学习物品表征,第二阶段在平衡的数据集上训练预测器(如分类器)。但是这种方法在推荐场景中,这种方法会导致严重的遗忘问题,即第一阶段学到的知识会在第二阶段遗忘。并且两阶段训练比联合训练的成本更高。而CDN则兼顾了解耦(decoupling)的思想,并克服了遗忘问题。
长尾问题分析
长尾问题的本质是什么呢?
先来抛个砖:个人认为长尾物品推荐效果不好的本质原因是否是因为物品的特征计算不准确,由于交互较少,按照正常的计算逻辑得到的结果是有偏(biased)的。感觉现在推荐里卷来卷去,如何去偏慢慢得到大家的重视了。
论文中,作者理论上分析(有点意思,具体分析可以参考论文,但是感觉有点牵强)得到长尾问题不利于整体效果的原因是因为对用户偏好的预测是有偏的,这个偏差又来自两部分(这里借鉴石塔西大佬的解释和观点2):
- 物品本身特征学习的质量与其分布有关。对于热门物品,是那些容易记忆的特征发挥作用,比如item id embedding,如果学好了,是最个性化的特征。但是对于长尾物品,恰恰是在模型看重这些特征上都没有学习好(因为缺少训练数据,不可能将长尾item id embedding学好)。
- 用户对物品的偏好不容易学好。训练集中正样本以热门物品居多,从而让user embedding也向那些高热物品靠拢,而忽视长尾物品。
对于第一种偏差,要解决模型对那些冷启友好特征不重视的问题。对于冷启,单单增加一些对冷启友好的特征是没用的,因为模型已经被老用户、老物料绑架了。以物料冷启为例,模型看重的item id embedding这些最个性化的物料特征,但是恰恰是长尾物品没有学好的。长尾物品希望模型多看重一些可扩展性好的特征,比如tag / category,但是模型却不看重。
CDN从以下两个方面解决长尾问题:
- 物品侧,解耦头部和尾部物品的表征的学习,即记忆(memorization)和泛化(generalization)解耦。具体做法是把记忆相关的特征和泛化相关的特征分别喂进两个MOE中,让这两个MOE分别专注于记忆和泛化,然后通过门控机制对二者的输出进行加权。
- 用户侧,通过正则化的双边分支网络(regularized bilateral branch network3)解耦用户的采样策略。该网络分成有两个分支,一个分支在全局数据上学习用户偏好,另一个分支在相对平衡的数据上学习。
CDN
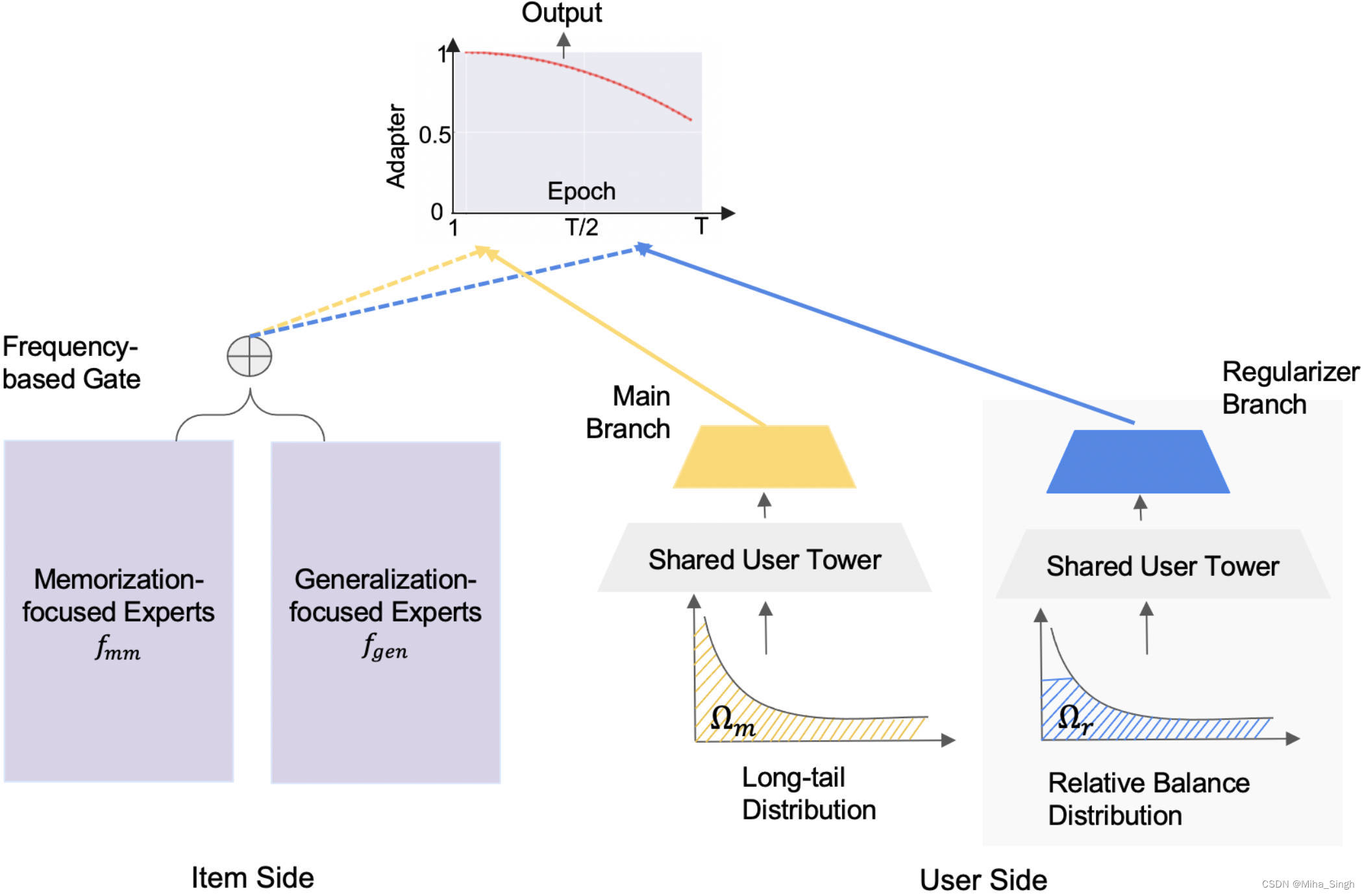
CDN的整体结构如上图所示,左右两边分别对应物品侧和用户侧。
Item Memorization and Generalization Decoupling
既然要通过划分记忆和繁华特征来解耦,那么怎么划分输入的特征呢?
记忆特征(Memorization features)
记忆特征使模型能够记住数据集中出现频繁的模式,通常是满足以下性质的类别特征:
- Uniqueness。对于特征空间 V \mathcal{V} V,存在单射函数 f i n : I → V f_{in}:\ \mathcal{I} \rightarrow \mathcal{V} fin: I→V;
- Independence,即特征空间的任意两个元素之间是独立的,互不影响的。
对于记忆特征的embedding,其一般只会被指定的物品更新(uniqueness),并且不同物品的记忆特征一般不同(independence)。因此,记忆特征一般只记住与物特定品相关的信息。物品ID就是一种很强的记忆特征(还有哪些记忆特征呢?)。
泛化特征(Generalization features)
泛化特征通常是那些能学习到用户偏好和物品之间关系的特征,这些特征通常是物品间共享的特征,如物品的类别、标签等。
物品表征学习
作者采用基于频率的门控的MoE(Mixture of Expert)来解耦记忆和泛化。
对于一个训练样本
(
u
,
i
)
(u, i)
(u,i),物品表征表示如下(方便起见,向量没有用黑体):
y
=
∑
k
=
1
n
1
G
(
i
)
k
E
k
m
m
(
i
m
m
)
+
∑
k
=
n
1
+
1
n
1
+
n
2
G
(
i
)
k
E
k
g
e
n
(
i
g
e
n
)
y = \sum_{k=1}^{n_1} G(i)_k E_k^{mm}(i_{mm}) + \sum_{k=n_1 + 1}^{n_1 + n_2} G(i)_k E_k^{gen}(i_{gen})
y=k=1∑n1G(i)kEkmm(imm)+k=n1+1∑n1+n2G(i)kEkgen(igen)
其中
E
k
m
m
(
⋅
)
E_k^{mm}(\cdot)
Ekmm(⋅)表示专注于记忆的第
k
k
k个专家网络,输入为记忆特征
i
m
m
i_{mm}
imm;
E
k
g
e
n
(
⋅
)
E_k^{gen}(\cdot)
Ekgen(⋅)表示专注于泛化的第
k
k
k个专家网络,输入为泛化特征
i
g
e
n
i_{gen}
igen。注意,这些特征一般是把对应特征的嵌入拼接起来。
G
(
⋅
)
G(\cdot)
G(⋅)为门控函数(输出为向量),
G
(
i
)
k
G(i)_{k}
G(i)k表示门控输出的第
k
k
k个元素,且
∑
k
=
1
n
1
+
n
2
G
(
i
)
=
1
\sum_{k=1}^{n_1 + n_2} G(i) = 1
∑k=1n1+n2G(i)=1。简单的理解,就是门控的输出对记忆和泛化网络的输出进行动态加权。此处的动态加权即是关键,即根据物品的热度动态调整记忆和泛化的比例。作者建议用物品频率作为门控的输入,即
g
(
i
)
=
s
o
f
t
m
a
x
(
W
i
f
r
e
q
)
g(i) = softmax(W i_{freq})
g(i)=softmax(Wifreq)。
记忆和泛化解耦后,泛化的专家网络的更新将主要来自于长尾物品,而不会损害记忆专家网络从而导致整体性能的下降。
User Sample Decoupling
这一部分解耦的是用户的交互,提出了正则化的双边网络(Regularized Bilateral Branch Network):
- main分支在原始数据 Ω m \Omega_m Ωm上训练。显然这个数据集中物品的交互是有偏的,这对用户在长尾物品上的偏好的学习是有偏的;
- regularizer分支在均衡后的数据上 Ω r \Omega_r Ωr训练,即对热门物品的交互进行降采样。显然,用户对长尾物品的偏好学习被提权了。
这两个分支有一个共享的基座(User Tower),以及各自一个分支特定的网络。在训练阶段,对于
(
u
m
,
i
m
)
∈
Ω
m
(u_m, i_m) \in \Omega_m
(um,im)∈Ωm和
(
u
r
,
i
r
)
∈
Ω
r
(u_r, i_r) \in \Omega_r
(ur,ir)∈Ωr分别进入main和regularizer分支,不同分支计算出来的用户表示为:
x
m
=
h
m
(
f
(
u
m
)
)
,
x
r
=
h
r
(
f
(
u
r
)
)
x_m = h_m(f(u_m)),\ x_r = h_r(f(u_r))
xm=hm(f(um)), xr=hr(f(ur))
其中
f
(
⋅
)
f(\cdot)
f(⋅)就是两个分支共享的基座,
h
m
(
⋅
)
,
h
r
(
⋅
)
h_m(\cdot), h_r(\cdot)
hm(⋅),hr(⋅)分别是两个分支特有的。main和regularizer可以同时训练,但是在推理时只使用main分支。
Cross Learning
最终物品和用户的表征通过一个
γ
\gamma
γ-adapter来融合,并控制训练过程中模型的注意力转移到长尾物品上。训练时的logit计算方式为:
s
(
i
m
,
i
r
)
=
α
t
y
m
T
x
m
+
(
1
−
α
t
)
y
r
T
x
r
s(i_m, i_r) = \alpha_t y_m^T x_m + (1 - \alpha_t) y_r^T x_r
s(im,ir)=αtymTxm+(1−αt)yrTxr
其中
α
t
\alpha_t
αt就是
γ
\gamma
γ-adapter,它是训练轮数的函数:
α
t
=
1
−
(
t
γ
×
T
)
2
,
γ
>
1
\alpha_t = 1 - (\frac{t}{\gamma \times T})^2,\ \gamma > 1
αt=1−(γ×Tt)2, γ>1
其中
T
T
T是总的训练轮数,
t
t
t是当前轮数,
γ
\gamma
γ是正则化率,对于越不平衡的数据集,
γ
\gamma
γ的取值一般越大。得到
s
(
i
m
,
i
r
)
s(i_m, i_r)
s(im,ir)后,用户对物品的偏好通过以下方式计算:
p
(
i
∣
u
)
=
e
s
(
i
m
,
i
r
)
∑
j
∈
I
e
s
(
j
m
,
j
r
)
p(i | u) = \frac{e^{s(i_m, i_r)}} {\sum_{j \in \mathcal{I}} e^{s(j_m, j_r)}}
p(i∣u)=∑j∈Ies(jm,jr)es(im,ir)
损失函数为:
L
=
−
∑
u
∈
U
,
i
∈
I
α
t
d
^
(
u
m
,
i
m
)
l
o
g
p
(
i
∣
u
)
+
(
1
−
α
t
)
d
^
(
u
r
,
i
r
)
l
o
g
p
(
i
∣
u
)
=
−
∑
u
∈
U
,
i
∈
I
l
o
g
p
(
i
∣
u
)
[
α
t
d
^
(
u
m
,
i
m
)
+
(
1
−
α
t
)
d
^
(
u
r
,
i
r
)
]
\begin{align} L &= - \sum_{u \in \mathcal{U}, i \in \mathcal{I}} \alpha_t\ \hat{d}(u_m, i_m)\ log p(i | u) + (1 - \alpha_t)\ \hat{d}(u_r, i_r)\ log p(i | u) \\ &= - \sum_{u \in \mathcal{U}, i \in \mathcal{I}} log p(i | u)\ [\alpha_t\ \hat{d}(u_m, i_m) + (1 - \alpha_t)\ \hat{d}(u_r, i_r)] \end{align}
L=−u∈U,i∈I∑αt d^(um,im) logp(i∣u)+(1−αt) d^(ur,ir) logp(i∣u)=−u∈U,i∈I∑logp(i∣u) [αt d^(um,im)+(1−αt) d^(ur,ir)]
其中
d
^
(
u
m
,
i
m
)
,
d
^
(
u
r
,
i
r
)
∈
{
0
,
1
}
\hat{d}(u_m, i_m), \hat{d}(u_r, i_r) \in \{0, 1\}
d^(um,im),d^(ur,ir)∈{0,1}分别表示
Ω
m
,
Ω
r
\Omega_m, \Omega_r
Ωm,Ωr中的用户偏好(这里论文描述的不是很清楚)。
吐槽以下:论文在训练数据构造和训练过程讲的都不是很清楚。比如同时训练main和regularizer,输入的样本分别是什么, u m , u r u_m, u_r um,ur是同一个用户吗, i m , i r i_m, i_r im,ir是用一个物品吗?还有就是 s ( i m , i r ) s(i_m, i_r) s(im,ir)计算结果是什么含义?
总结
总体来说,这篇论文对长尾问题的认识还是很深的,也确实让人有所启发。特别关于特征解耦的那一部分,感觉以后可以实践一下。但是在后续的两个分支部分语焉不详,且缺乏相关的实现细节,或许是本人公里不够,一些细节错过了。还请路过的大佬指正。
参考
Decoupling representation and classifier for long-tailed recognition, ICLR 2020. ↩︎
https://zhuanlan.zhihu.com/p/651731184:似曾相识:谈Google CDN长尾物料推荐. ↩︎
BBN: Bilateral-Branch Network with Cumulative Learning for Long-Tailed Visual Recognition, CVPR 2020. ↩︎



![[杂谈]-2023年实现M2M的技术有哪些?](https://img-blog.csdnimg.cn/aba543cbcd674f5a86a4f8003b474fa6.webp#pic_center)