contents
- hw9 - Back Propagation Through Time
- task1
- 题目内容
- 题目思路+题目解答
- 题目总结
- task2
- 题目内容
- 题目思路+题目解答
- 题目总结
hw9 - Back Propagation Through Time
task1
题目内容
推导RNN反向传播算法BPTT。
题目思路+题目解答
首先我们要清楚RNN进行前向传播的过程:
- 由输入层→state层: 输入层部分除了原始的输入资料外会再加上t-1时间的state状态,一同向前传递到t时间的state。
- state层→输出层: 这边向前传递就什么特殊的部分,跟一般MLP差不多。


由此得到如下推导

题目总结
本题考查的是对于循环神经网络的随时间反向传播过程推导,要了解计算的过程。
task2
题目内容
设计简单RNN模型,分别用Numpy、Pytorch实现反向传播算子,并代入数值测试。
题目思路+题目解答
本题承接上一题的推导过程,形成代码即可。
我们这边还是继承自自造轮子的基类LayerBase,代码如下:
class RNN(LayerBase):
activation_functions = {
'tanh':tanh
}
def __init__(self, n_hidden_states, activation='tanh', n_bptt_steps=5, input_shape=None):
self.input_shape = input_shape
self.n_hidden_states = n_hidden_states
self.activation = RNN.activation_functions[activation]()
self.trainable = True
self.n_bptt_steps = n_bptt_steps
self.W = None # 前一状态权重
self.V = None # 输出权重
self.U = None # 输入权重
def init(self, optimizer):
timesteps, input_dim = self.input_shape
limit = 1 / math.sqrt(input_dim)
self.U = np.random.uniform(-limit, limit, (self.n_hidden_states, input_dim))
limit = 1 / math.sqrt(self.n_hidden_states)
self.V = np.random.uniform(-limit, limit, (input_dim, self.n_hidden_states))
self.W = np.random.uniform(-limit, limit, (self.n_hidden_states, self.n_hidden_states))
self.U_opt = copy.copy(optimizer)
self.V_opt = copy.copy(optimizer)
self.W_opt = copy.copy(optimizer)
def forward(self, X, training=True):
self.layer_input = X
batch_size, timesteps, input_dim = X.shape
# 保存用于在反向传播中使用的值
self.state_input = np.zeros((batch_size, timesteps, self.n_hidden_states))
self.states = np.zeros((batch_size, timesteps+1, self.n_hidden_states))
self.outputs = np.zeros((batch_size, timesteps, input_dim))
# 将最后一个时间步设置为零以计算时间步为零的 state_input
self.states[:, -1] = np.zeros((batch_size, self.n_hidden_states))
for t in range(timesteps):
# state_t 的输入是当前输入和前时刻的输出
self.state_input[:, t] = X[:, t].dot(self.U.T) + self.states[:, t-1].dot(self.W.T)
self.states[:, t] = self.activation(self.state_input[:, t])
self.outputs[:, t] = self.states[:, t].dot(self.V.T)
return self.outputs
def backward(self, accum_grad):
_, timesteps, _ = accum_grad.shape
# 我们保存每个参数的累积梯度的变量
grad_U = np.zeros_like(self.U)
grad_V = np.zeros_like(self.V)
grad_W = np.zeros_like(self.W)
# 层输入的梯度将会传递到网络中的上一层
accum_grad_next = np.zeros_like(accum_grad)
# BPTT
for t in reversed(range(timesteps)):
# 在时间步 t 更新梯度 V
grad_V += accum_grad[:, t].T.dot(self.states[:, t])
# 基于状态输入计算梯度
grad_wrt_state = accum_grad[:, t].dot(self.V) * self.activation.gradient(self.state_input[:, t])
# 层输入梯度
accum_grad_next[:, t] = grad_wrt_state.dot(self.U)
# 通过反向传播更新 W 和 U 的梯度,至多至时间 t
for t_ in reversed(np.arange(max(0, t - self.n_bptt_steps), t+1)):
grad_U += grad_wrt_state.T.dot(self.layer_input[:, t_])
grad_W += grad_wrt_state.T.dot(self.states[:, t_-1])
# 根据前面状态计算梯度
grad_wrt_state = grad_wrt_state.dot(self.W) * self.activation.gradient(self.state_input[:, t_-1])
# 更新权重
self.U = self.U_opt.update(self.U, grad_U)
self.V = self.V_opt.update(self.V, grad_V)
self.W = self.W_opt.update(self.W, grad_W)
return accum_grad_next
将随机数据传入,将自定义算子和torch算子的权重进行同步并运行,进行比较,得到:
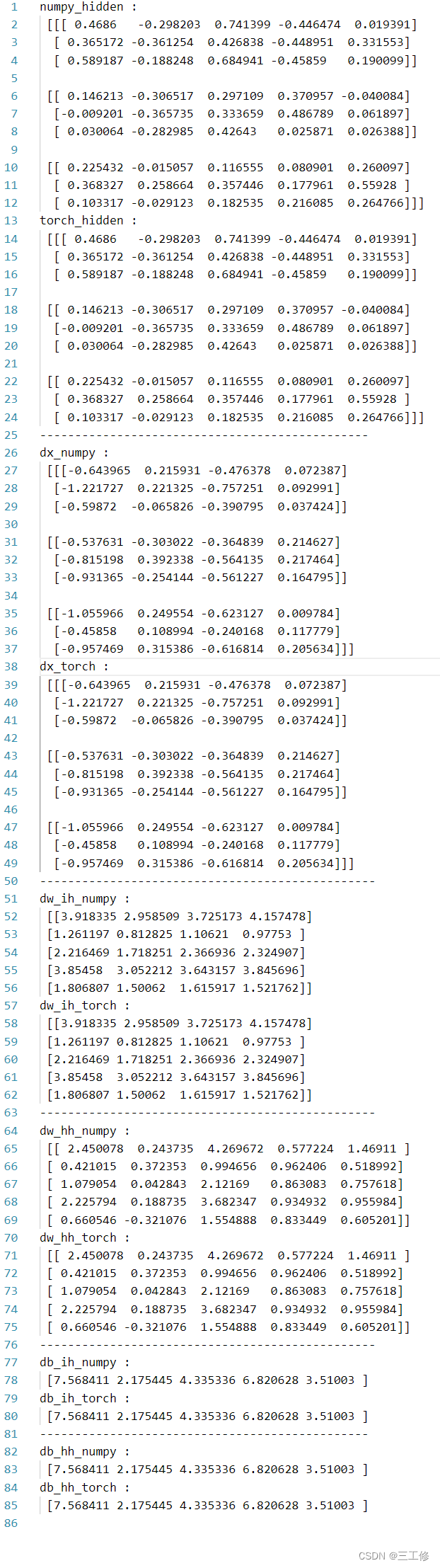
题目总结
本题考察的是依据之前的推导过程将理论变为代码的能力。
![[ 数据结构 -- 手撕排序算法第二篇 ] 冒泡排序](https://img-blog.csdnimg.cn/857becdeaf3b4f7a981da7eb40335ccb.png)

![[附源码]Python计算机毕业设计Django万佳商城管理系统](https://img-blog.csdnimg.cn/cf1182f66a1b43399a5fe19654c445c0.png)



![[附源码]Python计算机毕业设计Django社区生活废品回收APP](https://img-blog.csdnimg.cn/a818fefbc1bd491a9b14cc7829ee3232.png)
![[附源码]Python计算机毕业设计Django室内设计类网站](https://img-blog.csdnimg.cn/01befbbb8adb4390aa3695be43fd6084.png)