前言

接上文，我们已经知道如何利用夹角余弦来计算两条轨迹的相似度，也知道其中优势和劣势，夹角余弦方法作为一个基础的baseline有其存在的价值，很多学者也提出了各式各样的改进方法来计算轨迹相似度，但是，在上文，我们也提到了在轨迹相似度计算的时候应该尽量使用与轨迹点直接关系的测度，如轨迹点的数目等，而不应该使用有轨迹点组合而成的几何对象，如线，面，多边形等。也就是回归事务数据本源，而不应该为了对比相似性而七拼八凑，这样反而回来带杂质，测度的不准。这一节，我们就来利用缓冲原理计算轨迹相似度。

预备知识

我们在GIS分析的时候，经常会对一个对象做缓冲来看其影响范围，而轨迹具有线性特质，现在，将如下轨迹L

$[p_1,p_2, \cdots, p_n]$

其中， $p_i（1\leq i\leq n）$ 表示第i个轨迹点的位置信息 $p_i=[lng_i, lat_i]$ ，改成集合形式

$\{p_i|1\leq i \leq n\}$

如果对 $L$ 进行一定范围 $\delta$ 的缓冲的话会形成一条固定宽度的长带

$\hat{L} = \{ s|d(s,L)<\delta\}$

有另一条轨迹 $Q$
$[q_1,q_2, \cdots, q_n]$
如果 $Q$ 有一些点有落在这个长带 $\hat{L}$ 范围里面，我们可以称 $Q$ 的这些点为 $L$ 这条轨迹可触达的点, $Q$ 与 $L$ 存在相似性，如果 $Q$ 没有轨迹点落在这个长带范围里面，则称 $Q$ 与 $L$ 不存在相似性。

思路与核心代码

既然两条轨迹的相似度与其可触达点有密切关系，那么，可以定义两条轨迹的相似度计算公式

$\lambda_1 \frac{|L_Q|}{|L|} +\lambda_2 \frac{|Q_L|}{|Q|}$

其中， $L_Q$ 表示轨迹 $L$ 被轨迹 $Q$ 缓冲出的可触达的点做成的集合， $Q_L$ 表示轨迹 $Q$ 被轨迹 $L$ 缓冲出的可触达的点做成的集合， $∣ L ∣$ 表示轨迹 $L$ 的轨迹点的个数， $∣ Q ∣$ 表示轨迹 $Q$ 的轨迹点的个数， $\lambda_i$ 表示各自对应可触达点的权重，可以是每条轨迹点的占所有轨迹点的比重；

def toleranceTest(traj1, traj2): #容差检测，检测两条轨迹的对应轨迹点的距离，并给出缓冲范围的建议值
    max_lng = np.max([traj1['lng'].max(), traj2['lng'].max()])
    min_lng = np.min([traj1['lng'].min(), traj2['lng'].min()])
    max_lat = np.max([traj1['lat'].max(), traj2['lat'].max()])
    min_lat = np.min([traj1['lat'].min(), traj2['lat'].min()])
    dot1 = [min_lng, min_lat]
    dot2 = [max_lng, min_lat]
    dot3 =  [max_lng,  max_lat]
    dot4  = [min_lng, max_lat]
    rectangle = Polygon([dot1, dot2, dot3, dot4])
    area = rectangle.area
    # print("所在区域范围面积", area)
    if  area< 0.00001:
        eps = 0.0001 #10米
    elif area<0.0001:
        eps = 0.0002 #20米
    elif area<0.001:
        eps = 0.0003 #30米
    elif area<0.01:
        eps = 0.0004 #40米
    elif area<0.1:
        eps = 0.0005 #50米
    elif area<1:
        eps = 0.001 #100米
    else:
        eps = 0.0015 #150米
    # print("缓冲宽度", eps)
    return eps

def bufferSimilarity(traj1, traj2, eps): #缓冲相似度
    traj1_points  = list(zip(traj1['lng'], traj1['lat']))
    traj2_points  = list(zip(traj2['lng'], traj2['lat']))
    traj1_line = LineString(traj1_points)
    traj2_line = LineString(traj2_points)
    traj1_buffer = traj1_line.buffer(eps) #缓冲50米
    traj2_buffer = traj2_line.buffer(eps) #缓冲50米
    traj1_buffer_cnt = 0 #轨迹1缓冲的点
    traj2_buffer_cnt = 0 #轨迹2缓冲的点数
    for point in traj2_points:
        if traj1_buffer.contains(Point(point)):  # True or False
            traj1_buffer_cnt +=1
    for point in traj1_points:
        if traj2_buffer.contains(Point(point)):
            traj2_buffer_cnt +=1
    buffer_sim_value = (traj1_buffer_cnt/len(traj2_points)*(len(traj2_points)/(len(traj1_points)+len(traj2_points))))+\
                        (traj2_buffer_cnt/len(traj1_points)*(len(traj1_points)/(len(traj1_points)+len(traj2_points))))
    print("缓冲相似度", buffer_sim_value)
    return buffer_sim_value

优缺点分析

考虑到轨迹跨度范围的不同，有些轨迹可能只有几公里，有些几十公里，有些却有上百公里，不同跨度所需要的缓冲宽度也是不一样的，为此，可以设计一个容差检测，其目的是为不同长度的轨迹对比提供一个缓冲宽度参考，直白一点的就是长的轨迹，缓冲宽一点，短的轨迹缓冲窄一点，这种映射关系可以设计成压缩映射，可以找轨迹范围四至的面积作为标的标的物比，具体见toleranceTest函数，主函数就是把两者相互缓冲对方的轨迹点计算出来，然后利用类似杰卡德公式来计算两条轨迹的相似度。

数值实验

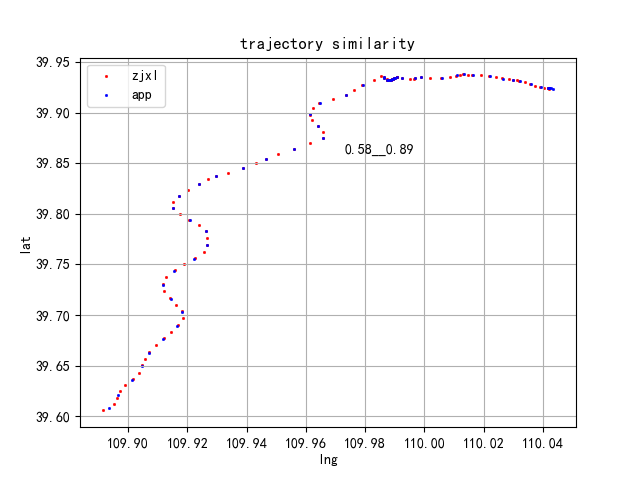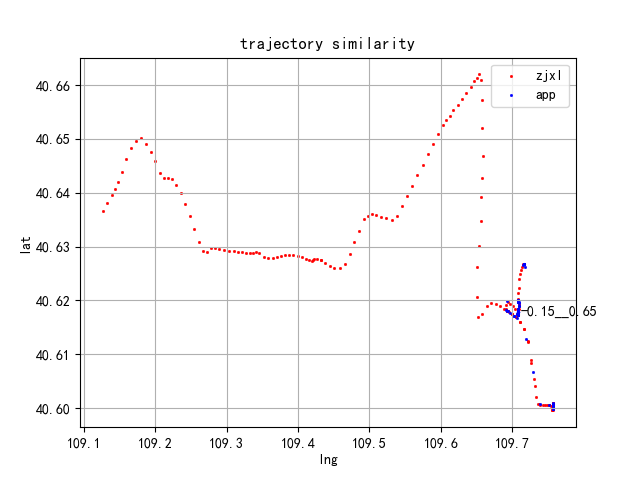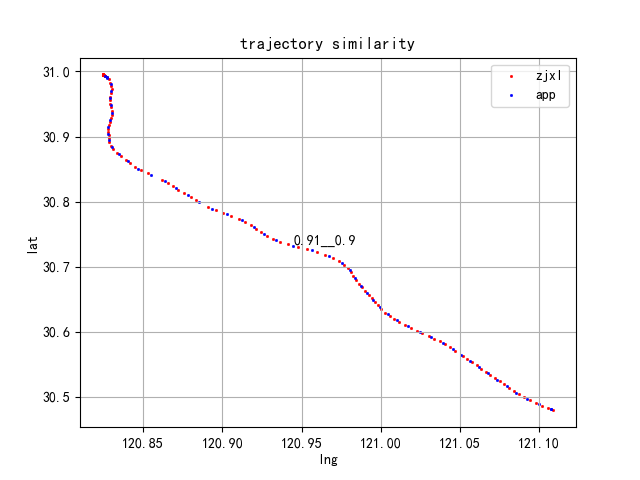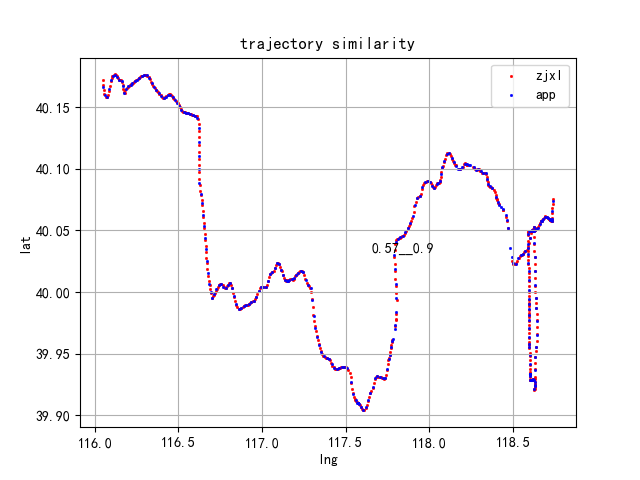
下面是对不同运单利用缓冲原理计算出来的相似度对比，整体还不错，既考虑了相互对称性，有考虑各自轨迹点数的影响，具有很好的均衡性和稳健性。
缓冲相似度

参考文献

1，轨迹相似性度量方法
https://blog.csdn.net/weixin_39910711/article/details/109333641
2，【ST】轨迹相似性度量
https://zhuanlan.zhihu.com/p/384362352
3，轨迹相似性度量
https://zhuanlan.zhihu.com/p/148797145
4，向量相似度
https://blog.csdn.net/Gentleman_Qin/article/details/110465518
5，shapely官方文档
https://www.osgeo.cn/pygis/shapely.html
6，经纬度保留到不同小数位对应的精度
https://blog.csdn.net/qq_39805362/article/details/117329099