300.最长递增子序列

文章讲解：代码随想录 (programmercarl.com)

题目链接：300. 最长递增子序列 - 力扣（LeetCode）

题目：

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

分析：

dp[i]的定义

dp[i]表示i之前包括i的以nums[i]结尾最长上升子序列的长度
状态转移方程

位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。

所以：if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);

注意这里不是要dp[i] 与 dp[j] + 1进行比较，而是我们要取dp[j] + 1的最大值。
dp[i]的初始

每一个i，对应的dp[i]（即最长上升子序列）起始大小至少都是1.
确定遍历顺序

dp[i] 是有0到i-1各个位置的最长升序子序列推导而来，那么遍历i一定是从前向后遍历。

j其实就是0到i-1，遍历i的循环在外层，遍历j则在内层
举例推导dp数组

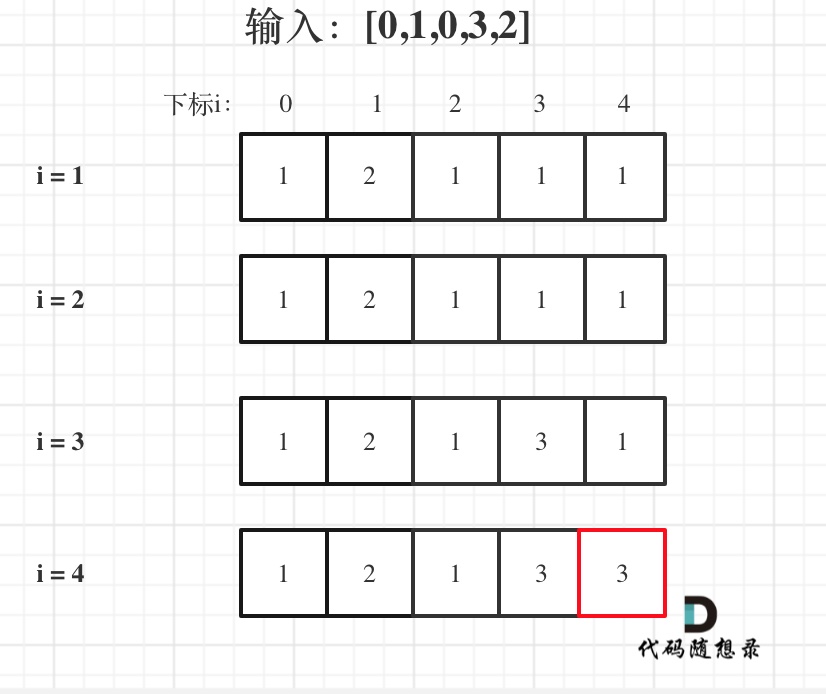
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if (nums.size() <= 1) return nums.size();
        vector<int> dp(nums.size(), 1);
        int result = 0;
        for (int i = 1; i < nums.size(); i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
            }
            if (dp[i] > result) result = dp[i];
        }
        return result;
    }
};

674.最长连续递增序列

文章讲解：代码随想录 (programmercarl.com)

题目链接：674. 最长连续递增序列 - 力扣（LeetCode）

题目：

给定一个未经排序的整数数组，找到最长且连续递增的子序列，并返回该序列的长度。

连续递增的子序列可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列。

分析：

确定dp数组（dp table）以及下标的含义

dp[i]：以下标i为结尾的数组的连续递增的子序列长度为dp[i]。
确定递推公式

如果 nums[i + 1] > nums[i]，那么以 i+1 为结尾的数组的连续递增的子序列长度一定等于以i为结尾的数组的连续递增的子序列长度 + 1 。

即：dp[i + 1] = dp[i] + 1;
dp数组如何初始化

以下标i为结尾的数组的连续递增的子序列长度最少也应该是1，即就是nums[i]这一个元素。

所以dp[i]应该初始1;
确定遍历顺序

从递推公式上可以看出， dp[i + 1]依赖dp[i]，所以一定是从前向后遍历。
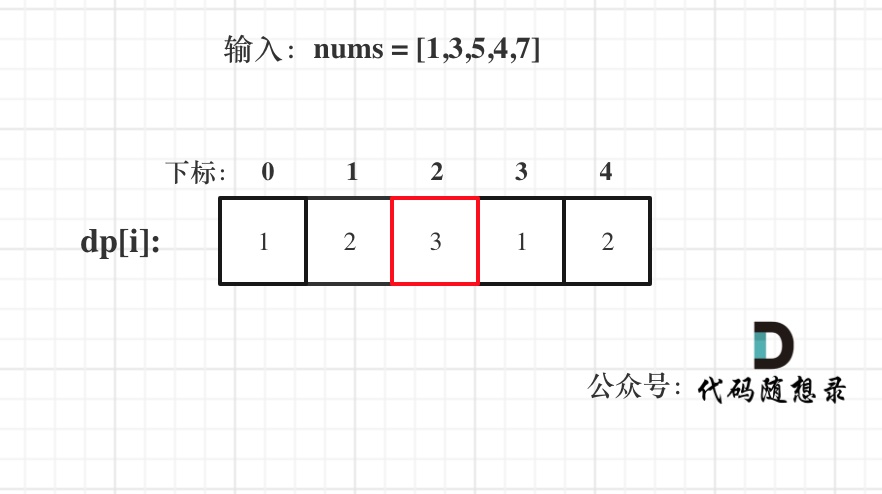
举例推导dp数组

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        if (nums.size() <= 1) return nums.size();
        vector<int> dp(nums.size(), 1);
        int result = 1;
        for (int i = 1; i < nums.size(); i++) {
            if (nums[i] > nums[i - 1]) {
                dp[i] = dp[i - 1] + 1;
            }
            if (dp[i] > result) result = dp[i];
        }
        return result;
    }
};

718.最长重复子数组

文章讲解：代码随想录 (programmercarl.com)

题目链接：718. 最长重复子数组 - 力扣（LeetCode）

题目：

给两个整数数组 A 和 B ，返回两个数组中公共的、长度最长的子数组的长度。

分析：

确定dp数组（dp table）以及下标的含义

dp[i] [j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i] [j]。（特别注意： “以下标i - 1为结尾的A” 标明一定是以A[i-1]为结尾的字符串）
确定递推公式

根据dp[i] [j]的定义，dp[i] [j]的状态只能由dp[i - 1] [j - 1]推导出来。

即当A[i - 1] 和B[j - 1]相等的时候，dp[i] [j] = dp[i - 1] [j - 1] + 1;

根据递推公式可以看出，遍历i 和 j 要从1开始！
dp数组如何初始化

根据dp[i] [j]的定义，dp[i] [0] 和dp[0] [j]其实都是没有意义的！

但dp[i] [0] 和dp[0] [j]要初始值，因为为了方便递归公式dp[i] [j] = dp[i - 1] [j - 1] + 1;

所以dp[i] [0] 和dp[0] [j]初始化为0。
确定遍历顺序

外层for循环遍历A，内层for循环遍历B。

那又有同学问了，外层for循环遍历B，内层for循环遍历A。不行么？

也行，一样的，我这里就用外层for循环遍历A，内层for循环遍历B了。

同时题目要求长度最长的子数组的长度。所以在遍历的时候顺便把dp[i][j]的最大值记录下来。
举例推导dp数组

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
        int result = 0;
        for (int i = 1; i <= nums1.size(); i++) {
            for (int j = 1; j <= nums2.size(); j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                if (dp[i][j] > result) result = dp[i][j];
            }
        }
        return result;
    }
};