《机器人学一(Robotics(1))》_台大林沛群 第 4 周【机械臂 逆运动学】 Quiz 4

news2024/11/15 8:25:59
  • 待完善： 第6-8

谁做出来了，麻烦指下路，谢谢！

  • 第6-7： 连蒙带猜🤣
  • 第8： 猜不出来😂

coursera链接

文章目录

      • 第1题
      • 第2题
      • 第3题
      • 第4题
      • 第5题-8
        • 求解 θ3-θ1的 Python 代码
      • 第8题
        • 求解 θ4 - θ6的 Python 代码
        • Matlab代码_参考

第1题

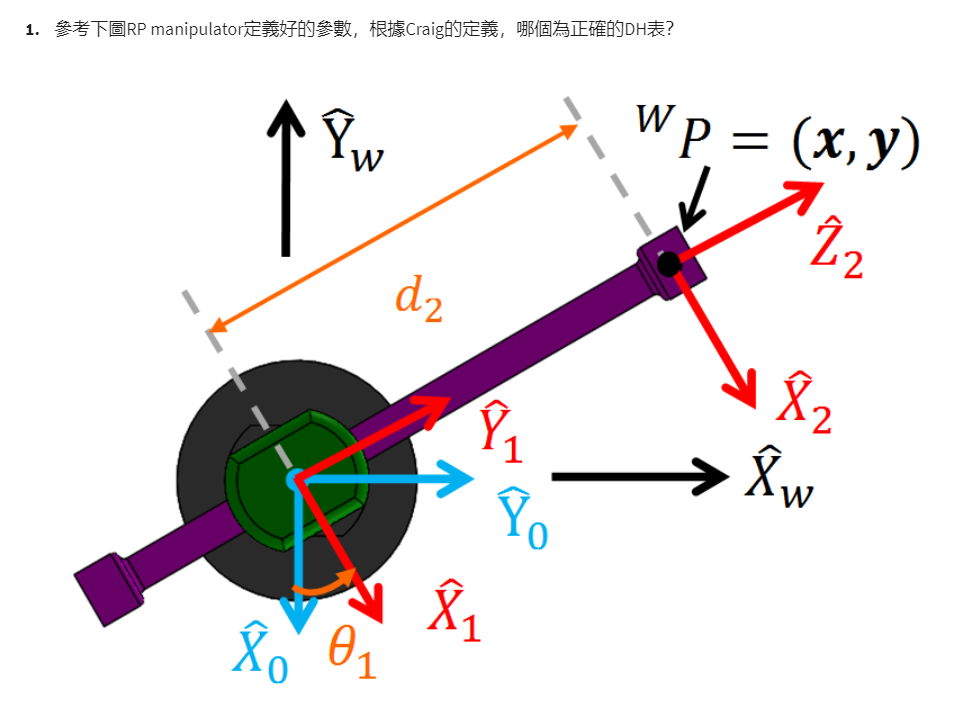
在这里插入图片描述
i = 2
1)、根据右手定则 ： 右手拇指(Z), 四指(X)，掌心朝向(Y)

  • Z 为 垂直 纸面 朝外

2)、右手拇指指向 X ^ 1 \hat{X}_{1} X^1​，将 Z ^ 1 \hat{Z}_{1} Z^1​旋转到 Z ^ 2 \hat{Z}_{2} Z^2​的方向，旋转方向与四指弯曲方向相反，为负， α为 -90。

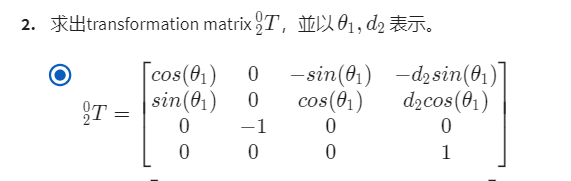
在这里插入图片描述

第2题

2、
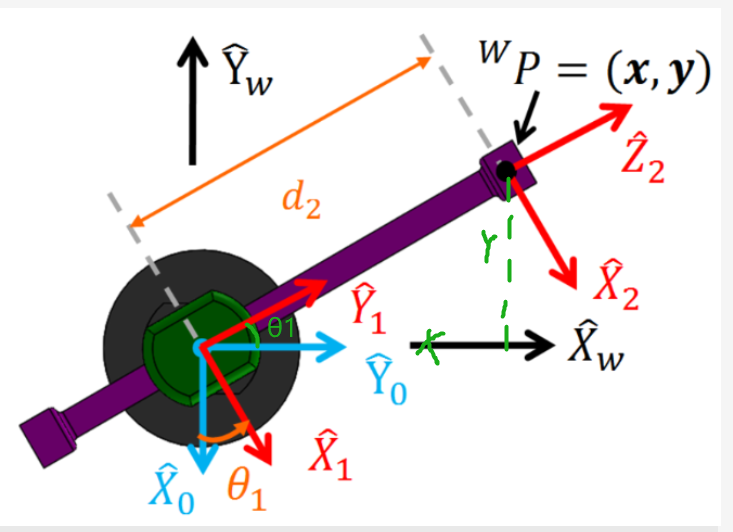
在这里插入图片描述
在这里插入图片描述

第3题

3、
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
t a n ( θ 1 ) = Y X tan(θ_1)=\frac{Y}{X} tan(θ1​)=XY​

import math
θ1 = 180 * math.atan(40/69.28)/ math.pi  ## 弧度转角度
print(θ1)  ## 30

答案： 30

找了半天公式的我🤣

第4题

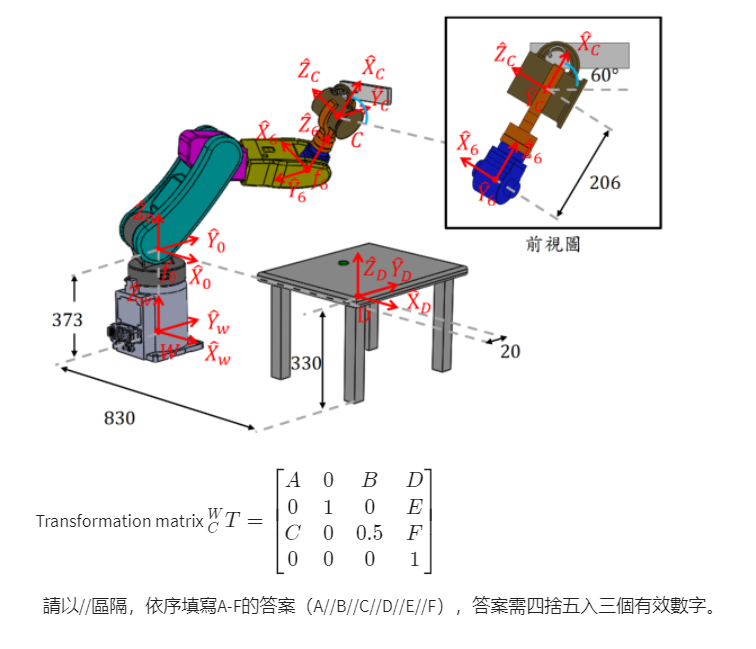
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
参考点： D(桌角) Desk
杯子——> 桌角——> 机械手
易于找到P， 用这个公式：
在这里插入图片描述
求R：
这里的转轴为 Y
注意角度的正负判断： 右手拇指指向Y， 四指弯曲方向为正
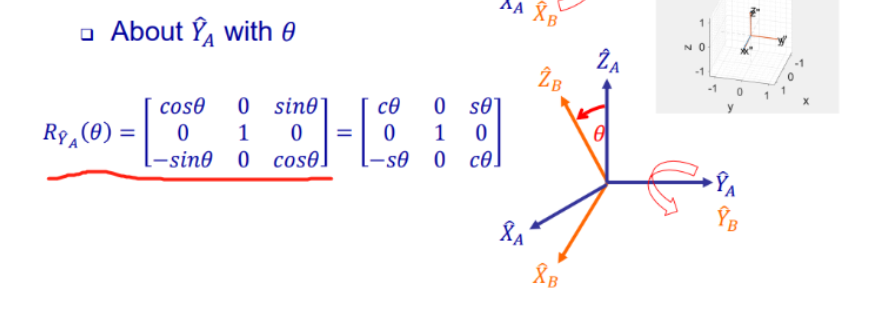
在这里插入图片描述

题中 右手拇指指向 Y ^ C \hat{Y}_C Y^C​ ， X ^ C \hat{X}_C X^C​ 相对于 X ^ D \hat{X}_D X^D​ 转向 与四指弯曲方向相反， 为负

import numpy as np 

## 无转动
R_WD = [[1, 0, 0],
       [0, 1, 0],
       [0, 0, 1]]
a = np.row_stack((R_WD,[[0, 0, 0]]))  ## 扩展 行
P = np.array([[830, 20, 330, 1]])
T_WD = np.column_stack((a,P.T))  ## 扩展 列， 注意 转置
# print(T_WD)


## 绕  Y轴 转
θ = np.pi * (-60)/180   ## 注意 正负 判断
R_DC = [[np.cos(θ), 0, np.sin(θ)],
       [0, 1, 0],
       [-np.sin(θ), 0, np.cos(θ)]]
# print(R_DC)

a = np.row_stack((R_DC,[[0, 0, 0]]))
P = np.array([[-500, 452, 410, 1]])
T_DC = np.column_stack((a,P.T))

T_WC = np.dot(T_WD, T_DC) 

T_WC = [[float(format(x, '.3g')) for x in T_WC[i]] for i in range(len(T_WC))]  ## 保留 3位有效数字
print(T_WC)

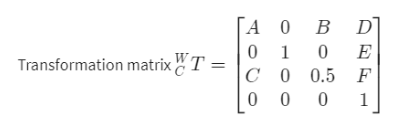
在这里插入图片描述在这里插入图片描述

答案： 0.5//-0.866//0.866//330//472//740

############################

补充： 课件里 是沿着 Z轴转

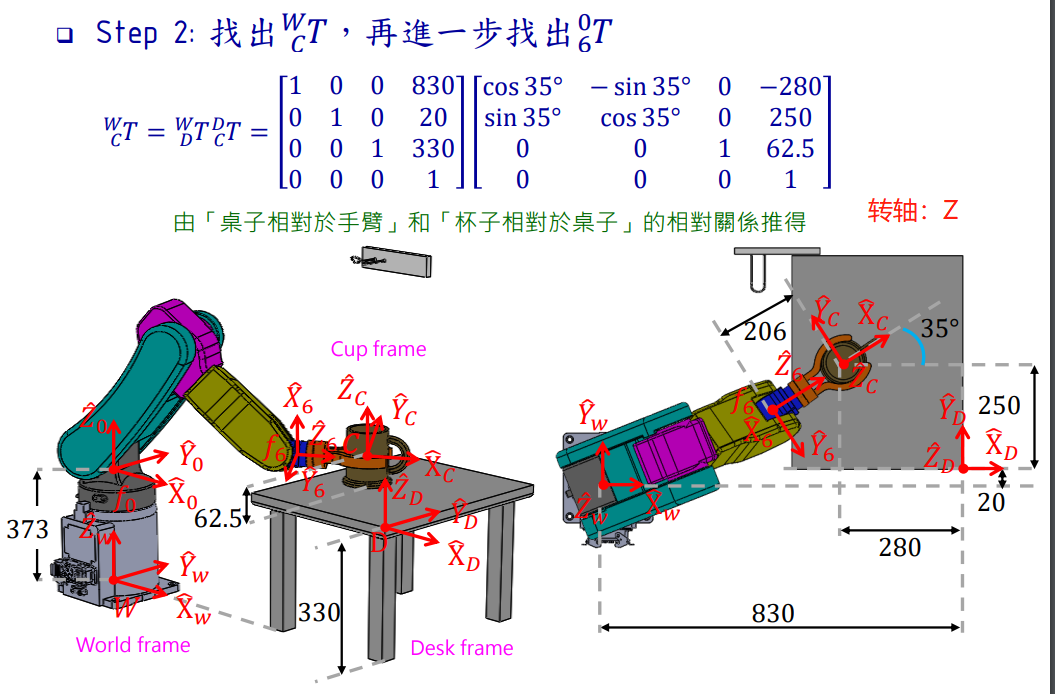
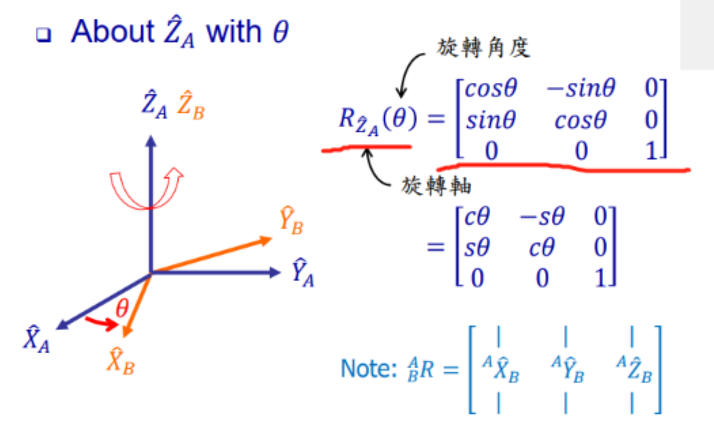
在这里插入图片描述

在这里插入图片描述
############################

第5题-8

在这里插入图片描述
参考 PPT Pieper’s Solution 部分， 题5-8一起做，因为由于 θ1的范围限制，可以排除一些 θ3 值。 但 θ2， θ1的选项仍有很多。
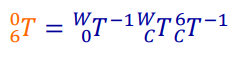
在这里插入图片描述

求解 θ3-θ1的 Python 代码

最终版本：

import numpy as np 

########################## 求 T_WC
## 无转动
R_WD = [[1, 0, 0],
       [0, 1, 0],
       [0, 0, 1]]
a = np.row_stack((R_WD,[[0, 0, 0]]))  ## 扩展 行
P = np.array([[830, 20, 330, 1]])
T_WD = np.column_stack((a,P.T))  ## 扩展 列， 注意 zhuan
# print(T_WD)


## 绕  Y轴 转
θ = np.pi * (-60)/180   ## 注意 正负 判断
R_DC = [[np.cos(θ), 0, np.sin(θ)],
       [0, 1, 0],
       [-np.sin(θ), 0, np.cos(θ)]]
# print(R_DC)

a = np.row_stack((R_DC,[[0, 0, 0]]))
P = np.array([[-500, 452, 410, 1]])
T_DC = np.column_stack((a,P.T))

T_WC = np.dot(T_WD, T_DC) 

# T_WC = [[float(format(x, '.3g')) for x in T_WC[i]] for i in range(len(T_WC))]  
# print(T_WC)   ## 第 4 题答案
#############################################

### 求 T_06

# 求 T_W0
# α, a, d, θ = 0, 0, 373, 0
## 无转动 
T_W0 = [[1, 0, 0, 0],
      [0, 1, 0, 0],
      [0, 0, 1, 373],
      [0, 0, 0, 1]]
# print(T_W0)

# 求 T_6C  Xc 和 Z6 方向相同，  Yc和 Y6 反向， Zc 和 X6 同向
T_6C = [[0, 0, 1, 0],
      [0, -1, 0, 0],
      [1, 0, 0, 206],
      [0, 0, 0, 1]]

T = np.dot(np.linalg.inv(T_W0), T_WC)
T_06 = np.dot(T, np.linalg.inv(T_6C))
# print(T_06)

P_04 = P_06 = np.array([[227, 472, 188.59876682, 1]])
x, y, z  = 227, 472, 188.59876682
################## 


α2, a2, d3 = 0, 340, 0   ## θ3
α3, a3, d4 = np.pi*(-90)/180, -40, 338   ## θ4
'''
## 仅与 θ3 有关
f1 = a3 * np.cos(θ3) + d4 * np.sin(α3)*np.sin(θ3) + a2 
#f2 = a3 * np.cos(α2)*np.sin(θ3) - d4 * np.sin(α3)*np.cos(α2)*np.cos(θ3) -\
#        d4 * np.sin(α2)*np.cos(α3) - d3 * np.sin(α2)
f2 = a3 * np.sin(θ3) - d4 * np.sin(α3) * np.cos(θ3)      
        
#f3 = a3 * np.sin(α2)* np.sin(θ3)- d4 * np.sin(α3)* np.sin(α2) * np.cos(θ3) + \
#       d4 * np.cos(α2) * np.cos(α3) + d3 * np.cos(α2)
f3 = d4 * np.cos(α3)
# print(f3)
'''
# 对 i= 1 i= 2
α0, a0, d1 = 0, 0, 0   ## θ1
α1, a1, d2 = np.pi*(-90)/180, -30, 0  ## θ2

'''
## 和 θ2，θ3有关
g1 = np.cos(θ2)* f1 - np.sin(θ2) * f2 + a1
# g2 = np.sin(θ2)* np.cos(α1) * f1 + np.cos(θ2) * np.cos(α1)* f2 -\
#      np.sin(α1) * f3 - d2 * np.sin(α1)
## 化简
g2 = np.sin(θ2)* np.cos(α1) * f1 + np.cos(θ2) * np.cos(α1)* f2 -\
     np.sin(α1) * f3
# g3 = np.sin(θ2)* np.sin(α1) * f1 + np.cos(θ2) * np.sin(α1)* f2 +\
#      np.cos(α1) * f3 + d2 * np.cos(α1)
## 化简
g3 = np.sin(θ2)* np.sin(α1) * f1 + np.cos(θ2) * np.sin(α1)* f2 +\
     np.cos(α1) * f3 

'''

'''
## a1 不等于 0 
k1 = f1 
k2 = -f2 
#k3 = f1**2 + f2**2 + f3**2 + a1**2 + d2**2 + 2*d2*f3
k3 = f1**2 + f2**2 + f3**2 + a1**2
#k4 = f3 * np.cos(α1) + d2 * np.cos(α1)
k4 = 0
'''

## 
r = x**2 + y**2 + z**2   ## 可解

'''
f1 = a3 * np.cos(θ3) + d4 * np.sin(α3)*np.sin(θ3) + a2
f2 = a3 * np.sin(θ3) - d4 * np.sin(α3) * np.cos(θ3) 
f3 = d4 * np.cos(α3)
k1 = f1 
k2 = -f2
k3 = f1**2 + f2**2 + f3**2 + a1**2
k4 = 0
'''

from sympy import *
θ3 = symbols('θ3')

f = (r-a1**2- (a3 * cos(θ3) + d4 * sin(α3)*sin(θ3) + a2 )**2 \
     - (a3 * sin(θ3) - d4 * sin(α3) * cos(θ3))**2 \
     - (d4 * cos(α3))**2 )**2/(4 * a1**2) \
  + z**2/(sin(α1))**2 \
  - (a3 * cos(θ3) + d4 * sin(α3)*sin(θ3) + a2)**2 \
  - (a3 * sin(θ3) - d4 * sin(α3) * cos(θ3))**2

# f = ((r - k3)**2)/(4*a1**2) + ((z-k4)**2)/(np.sin(α1))**2 - k1**2 - k2**2
root3 = solve([f],[θ3])
print('θ3(弧度值): ', root3)

# lis = [(-3.05085978803173,), (-2.76035600105476,), (-0.616827296276209,), (-0.326323509299240,)]
θ3_du = [180 * root3[i][0] / np.pi for i in range(len(root3))]  ## θ3 弧度换角度
print('θ3(以度为单位): ', θ3_du )  # [-174.801389740395, -158.156748814047, -35.3416007650924, -18.6969598387445]

## 求解 θ2
# 结果汇总
# θ3(以度为单位):  [-174.801389740395, -158.156748814047, -35.3416007650924, -18.6969598387445]
# θ3 = -3.05085978803173(无满足要求的θ1), -2.76035600105476(符合), -0.616827296276209(符合), -0.326323509299240(无满足要求的θ1)

# θ2 =[-2.82490122970046, -2.09516142685496],\
    # [0.207932140057394, 0.864458274997230]
    #  [-0.864458274997158, -0.207932140057458]

# θ3的有效解   -2.76035600105476 ,  -0.616827296276209 
θ3 =  -0.616827296276209 

f1 = a3 * np.cos(θ3) + d4 * np.sin(α3)*np.sin(θ3) + a2 
f2 = a3 * np.cos(α2)*np.sin(θ3) - d4 * np.sin(α3)*np.cos(α2)*np.cos(θ3) - d4 * np.sin(α2)*np.cos(α3) - d3 * np.sin(α2)
f3 = a3 * np.sin(α2)* np.sin(θ3)- d4 * np.sin(α3)* np.sin(α2) * np.cos(θ3) + d4 * np.cos(α2) * np.cos(α3) + d3 * np.cos(α2)

k1 = f1 
k2 = -f2 
k3 = f1**2 + f2**2 + f3**2 + a1**2 + d2**2 + 2*d2*f3

θ2 = symbols('θ2')

f = (k1 * cos(θ2) + k2 * sin(θ2)) * 2 * a1 + k3 - r
root2 = solve([f],[θ2])
θ2 = [root2[i][0] for i in range(len(root2))]
print(θ2)

# lis = [(-3.05085978803173,), (-2.76035600105476,), (-0.616827296276209,), (-0.326323509299240,)]
θ2_du = [180 * root2[i][0] / np.pi for i in range(len(root2))]  ## θ3 弧度换角度
print('θ2(以度为单位): ', θ2_du )  # [-174.801389740395, -158.156748814047, -35.3416007650924, -18.6969598387445]


## 求解  θ1 [-90, 90]
## 结果汇总
# θ2 = -2.82490122970046(不满足要求)
# θ1 = θ1(以度为单位):  [-115.684399755325, 115.684399755325] 
###
# θ2 = -2.09516142685496(不满足要求)
# θ1 = θ1(以度为单位):  [-115.684399755325, 115.684399755325]

################## θ31  满足
# θ2(以度为单位):  [11.9136340504118, 49.5298107225008]

# θ2 = 0.207932140057394
# θ1(以度为单位):  [-64.3156002446740, 64.3156002446740]

# θ2 = 0.864458274997230
# θ1(以度为单位):  [-64.3156002446740, 64.3156002446740]

################## θ32  
# [-0.864458274997158, -0.207932140057458]
# θ2(以度为单位):  [-49.5298107224966, -11.9136340504155]

# θ2 = -0.864458274997158 
# θ1(以度为单位):  [-64.3156002446747, 64.3156002446747]
# θ2 = -0.207932140057458
# θ1(以度为单位):  [-64.3156002446747, 64.3156002446747]

# θ33

θ2 = -0.207932140057458
g1 = np.cos(θ2)* f1 - np.sin(θ2) * f2 + a1
g2 = np.sin(θ2)* np.cos(α1) * f1 + np.cos(θ2) * np.cos(α1)* f2 -\
     np.sin(α1) * f3 - d2 * np.sin(α1)
g3 = np.sin(θ2)* np.sin(α1) * f1 + np.cos(θ2) * np.sin(α1)* f2 +\
     np.cos(α1) * f3 + d2 * np.cos(α1)

θ1 = symbols('θ1')

f = g1 * cos(θ1) - g2 * sin(θ1) - x
root1 = solve([f],[θ1])
θ1 = [root1[i][0] for i in range(len(root1))]
print(θ1)

# lis = [(-3.05085978803173,), (-2.76035600105476,), (-0.616827296276209,), (-0.326323509299240,)]
θ1_du = [180 * root1[i][0] / np.pi for i in range(len(root1))]  ## θ3 弧度换角度
print('θ1(以度为单位): ', θ1_du )  # [-174.801389740395, -158.156748814047, -35.3416007650924, -18.6969598387445]

### 根据实际，应使  θ1 = 64°

帮助理解

import numpy as np 

########################## 求 T_WC
## 无转动
R_WD = [[1, 0, 0],
       [0, 1, 0],
       [0, 0, 1]]
a = np.row_stack((R_WD,[[0, 0, 0]]))  ## 扩展 行
P = np.array([[830, 20, 330, 1]])
T_WD = np.column_stack((a,P.T))  ## 扩展 列， 注意 zhuan
# print(T_WD)


## 绕  Y轴 转
θ = np.pi * (-60)/180   ## 注意 正负 判断
R_DC = [[np.cos(θ), 0, np.sin(θ)],
       [0, 1, 0],
       [-np.sin(θ), 0, np.cos(θ)]]
# print(R_DC)

a = np.row_stack((R_DC,[[0, 0, 0]]))
P = np.array([[-500, 452, 410, 1]])
T_DC = np.column_stack((a,P.T))

T_WC = np.dot(T_WD, T_DC) 

# T_WC = [[float(format(x, '.3g')) for x in T_WC[i]] for i in range(len(T_WC))]  
# print(T_WC)   ## 第 4 题答案
#############################################

### 求 T_06

# 求 T_W0
# α, a, d, θ = 0, 0, 373, 0
## 无转动 
T_W0 = [[1, 0, 0, 0],
      [0, 1, 0, 0],
      [0, 0, 1, 373],
      [0, 0, 0, 1]]
# print(T_W0)

# 求 T_6C  Xc 和 Z6 方向相同，  Yc和 Y6 反向， Zc 和 X6 同向
T_6C = [[0, 0, 1, 0],
      [0, -1, 0, 0],
      [1, 0, 0, 206],
      [0, 0, 0, 1]]

T = np.dot(np.linalg.inv(T_W0), T_WC)
T_06 = np.dot(T, np.linalg.inv(T_6C))
# print(T_06)

P_04 = P_06 = np.array([[227, 472, 188.59876682, 1]])
x, y, z  = 227, 472, 188.59876682,
################## 
### 针对 i = 3, i = 4
α2, a2, d3 = 0, 340, 0   ## θ3
α3, a3, d4 = np.pi*(-90)/180, -40, 338   ## θ4

"""
## 仅与 θ3 有关
f1  = a3 * np.cos(θ3) + d4 * np.sin(α3)*np.sin(θ3) + a2 
# f2_θ3 = a3 * np.cos(α2)*np.sin(θ3) - d4 * np.sin(α3)*np.cos(α2)*np.cos(θ3) -\
#         d4 * np.sin(α2)*np.cos(α3) - d3 * np.sin(α2)
## 化简：
f2  = a3 * np.sin(θ3) - d4 * np.sin(α3) * np.cos(θ3)
# f3  = a3 * np.sin(α2)* np.sin(θ3)- d4 * np.sin(α3)* np.sin(α2) * np.cos(θ3) + \
#         d4 * np.cos(α2) * np.cos(α3) + d3 * np.cos(α2)
## 化简
f3 = d4 * np.cos(α3)  ## 2.069653090559027e-14   ## 可求
# print(f3)

"""
# 对 i= 1 i= 2
α0, a0, d1 = 0, 0, 0   ## θ1
α1, a1, d2 = np.pi*(-90)/180, -30, 0  ## θ2

"""
## 和 θ2，θ3有关
g1 = np.cos(θ2)* f1 - np.sin(θ2) * f2 + a1
# g2 = np.sin(θ2)* np.cos(α1) * f1 + np.cos(θ2) * np.cos(α1)* f2 -\
#      np.sin(α1) * f3 - d2 * np.sin(α1)
## 化简
g2 = np.sin(θ2)* np.cos(α1) * f1 + np.cos(θ2) * np.cos(α1)* f2 -\
     np.sin(α1) * f3
# g3 = np.sin(θ2)* np.sin(α1) * f1 + np.cos(θ2) * np.sin(α1)* f2 +\
#      np.cos(α1) * f3 + d2 * np.cos(α1)
## 化简
g3 = np.sin(θ2)* np.sin(α1) * f1 + np.cos(θ2) * np.sin(α1)* f2 +\
     np.cos(α1) * f3 


## a1 不等于 0 
k1 = f1 
k2 = -f2 
# k3 = f1**2 + f2**2 + f3**2 + a1**2 + d2**2 + 2*d2*f3
## 化简
k3 = f1**2 + f2**2 + f3**2 + a1**2
# k4 = f3 * np.cos(α1) + d2 * np.cos(α1)
## 化简
k4 = 0
"""

## 
r = x**2 + y**2 + z**2   ## 可解

# from scipy.optimize import fsolve
# def func(θ3):
#     return 


# root = solve([func], [θ3] )
# print(root)

from sympy import *
θ3 = symbols('θ3')

f = (r-a1**2- (a3 * cos(θ3) + d4 * sin(α3)*sin(θ3) + a2 )**2 - (a3 * sin(θ3) - d4 * sin(α3) * cos(θ3))**2 - (d4 * cos(α3))**2 )**2/(4 * a1**2) + z**2/(sin(α1))**2 - (a3 * cos(θ3) + d4 * sin(α3)*sin(θ3) + a2)**2 - (a3 * sin(θ3) - d4 * sin(α3) * cos(θ3))**2

root3 = solve([f],[θ3])
print('θ3(弧度值): ', root3)

# lis = [(-3.05085978803173,), (-2.76035600105476,), (-0.616827296276209,), (-0.326323509299240,)]
θ3_du = [180 * root3[i][0] / np.pi for i in range(len(root3))]  ## θ3 弧度换角度
print('θ3(以度为单位): ', θ3_du )  # [-174.801389740395, -158.156748814047, -35.3416007650924, -18.6969598387445]

## 求解 θ2
# 结果汇总
# θ3(以度为单位):  [-174.801389740395, -158.156748814047, -35.3416007650924, -18.6969598387445]
# θ3 = -3.05085978803173(无满足要求的θ1), -2.76035600105476(符合), -0.616827296276209(符合), -0.326323509299240(无满足要求的θ1)

# θ2 =[-2.82490122970046, -2.09516142685496],\
    # [0.207932140057394, 0.864458274997230]
    #  [-0.864458274997158, -0.207932140057458]

θ3 =  -0.326323509299240
f1  = a3 * np.cos(θ3) + d4 * np.sin(α3) * np.sin(θ3) + a2 
f2  = a3 * np.sin(θ3) - d4 * np.sin(α3) * np.cos(θ3)
f3 = d4 * np.cos(α3) 
k1 = f1 
k2 = -f2 
k3 = f1**2 + f2**2 + f3**2 + a1**2

θ2 = symbols('θ2')

f = (k1 * cos(θ2) + k2 * sin(θ2))*2 * a1 + k3 - r
root2 = solve([f],[θ2])
θ2 = [root2[i][0] for i in range(len(root2))]
print(θ2)

# lis = [(-3.05085978803173,), (-2.76035600105476,), (-0.616827296276209,), (-0.326323509299240,)]
θ2_du = [180 * root2[i][0] / np.pi for i in range(len(root2))]  ## θ3 弧度换角度
print('θ2(以度为单位): ', θ2_du )  # [-174.801389740395, -158.156748814047, -35.3416007650924, -18.6969598387445]


## 求解  θ1 [-90, 90]
## 结果汇总
# θ2 = -2.82490122970046(不满足要求)
# θ1 = θ1(以度为单位):  [-115.684399755325, 115.684399755325] 
###
# θ2 = -2.09516142685496(不满足要求)
# θ1 = θ1(以度为单位):  [-115.684399755325, 115.684399755325]

## θ31  满足
# θ2(以度为单位):  [11.9136340504118, 49.5298107225008]
# θ2 = 0.207932140057394
# θ1(以度为单位):  [-64.3156002446740, 64.3156002446740]

# θ2 = 0.864458274997230
# θ1(以度为单位):  [-64.3156002446740, 64.3156002446740]

# θ32  
# θ2 = -0.864458274997158 
# θ1(以度为单位):  [-64.3156002446747, 64.3156002446747]
# θ2 = -0.207932140057458
# θ1(以度为单位):  [-64.3156002446747, 64.3156002446747]

# θ33

θ2 = 2.82490122970057
g1 = np.cos(θ2)* f1 - np.sin(θ2) * f2 + a1
g2 = np.sin(θ2)* np.cos(α1) * f1 + np.cos(θ2) * np.cos(α1)* f2 -\
     np.sin(α1) * f3
g3 = np.sin(θ2)* np.sin(α1) * f1 + np.cos(θ2) * np.sin(α1)* f2 +\
     np.cos(α1) * f3 

θ1 = symbols('θ1')

f = g1 * cos(θ1) - g2 * sin(θ1) - x
root1 = solve([f],[θ1])
θ1 = [root1[i][0] for i in range(len(root1))]
print(θ1)

# lis = [(-3.05085978803173,), (-2.76035600105476,), (-0.616827296276209,), (-0.326323509299240,)]
θ1_du = [180 * root1[i][0] / np.pi for i in range(len(root1))]  ## θ3 弧度换角度
print('θ1(以度为单位): ', θ1_du )  # [-174.801389740395, -158.156748814047, -35.3416007650924, -18.6969598387445]

答案：-158//-35

第6题和第7题不理解正负怎么定的

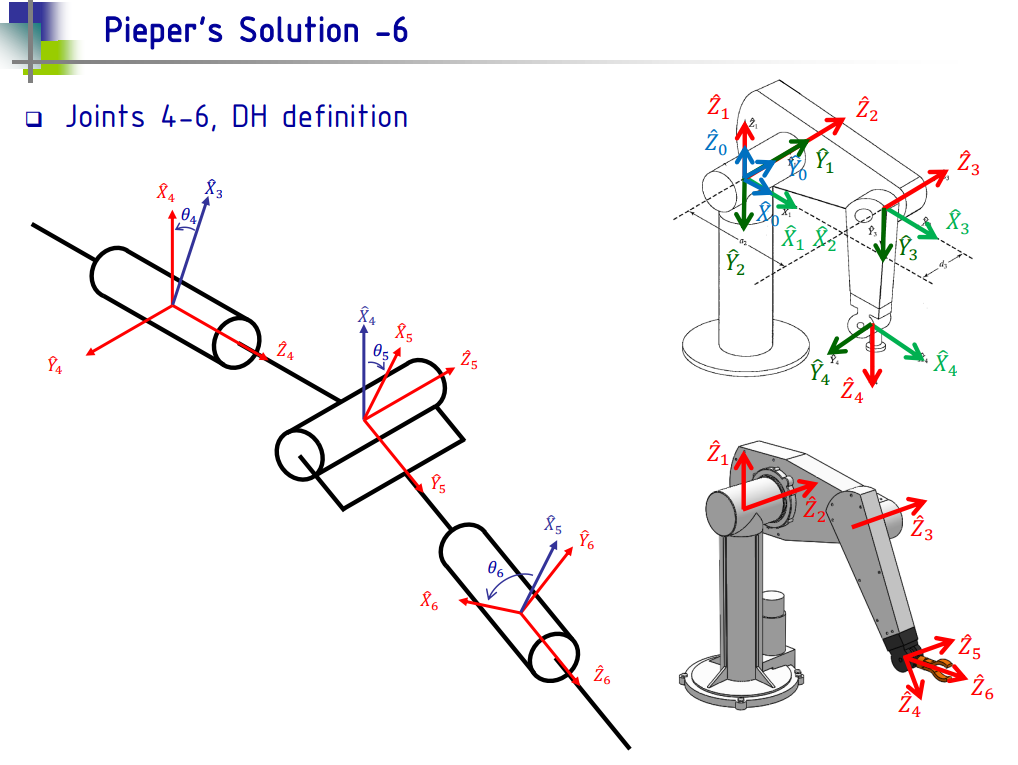
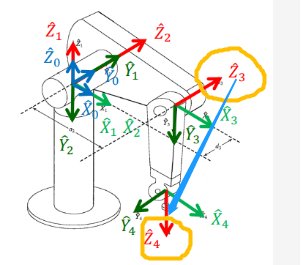
在这里插入图片描述
答案： 12//-50
在这里插入图片描述
答案： 64

第8题

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

求解 θ4 - θ6的 Python 代码

import numpy as np

#  求解  θ4, θ5, θ6   [-90, 90]

## 沿着 Z  旋转 x, 先旋转θ1， 再旋转 θ2, 再旋转 θ3, 
# θ1   θ1(以度为单位):  [-64.3156002446747, 64.3156002446747]
θ = -1.12251898466604  ##   可选 [-1.12251898466604, 1.12251898466604]
α = 0
R_01 = [[np.cos(θ), -np.sin(θ), 0],
       [np.sin(θ)*np.cos(α), np.cos(θ)*np.cos(α), -np.sin(α)],
       [np.sin(θ)*np.sin(α), np.cos(θ)*np.sin(α), np.cos(α)]]

# θ2 = np.pi * (-52.2)/180    ## 12//-50  -12  50
# 可选  4个
# [-0.864458274997158, -0.207932140057458]
# θ2(以度为单位):  [-49.5298107224966, -11.9136340504155]

# [0.864458274997158, 0.207932140057458]
# θ2(以度为单位):   [49.5298107224966, 11.9136340504155]

θ = -0.864458274997158  ## 
α = np.pi * (-90)/180
R_12 = [[np.cos(θ), -np.sin(θ), 0],
       [np.sin(θ)*np.cos(α), np.cos(θ)*np.cos(α), -np.sin(α)],
       [np.sin(θ)*np.sin(α), np.cos(θ)*np.sin(α), np.cos(α)]]

# θ3 = np.pi * (2.5)/180  ## -158//-35
## 可选 2个 

θ = -0.616827296276209 ## -2.76035600105476(符合), -0.616827296276209(符合)
α = 0
R_23 = [[np.cos(θ), -np.sin(θ), 0],
       [np.sin(θ)*np.cos(α), np.cos(θ)*np.cos(α), -np.sin(α)],
       [np.sin(θ)*np.sin(α), np.cos(θ)*np.sin(α), np.cos(α)]]

R = np.dot(R_01, R_12)
R_03 = np.dot(R, R_23)
# print(R_03)

## 由之前 计算的 T_06 
R_06 = [[ -0.8660254,  0. ,0.5],
        [  0., -1., 0.],
        [  0.5, 0., 0.8660254]]

R_36 = np.dot(np.linalg.inv(R_03), R_06)
# print(R_36)
r31 = R_36[2][0]
r32 = R_36[2][1]
r33 = R_36[2][2]
r23 = R_36[1][2]
r13 = R_36[0][2]
import math
β = math.atan2(math.sqrt(r31**2 + r32**2), r33)  ## 此外， 当 β 选负时，还有 一种 姿态选项， 而后续的θ4和 θ6 仅与 β的选值有关
β = -β  ## 另一组姿态
print(β)  ## 1.1033617668479667  63
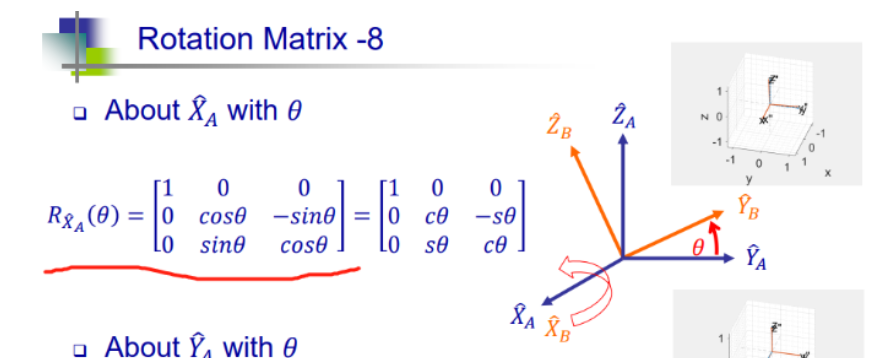
## 由PPT P25 DH定义  与 ZYZ 欧拉角度  转换关系
print('θ5：',180*β/np.pi)

# β = 1.1033617668479667
α = math.atan2(r23/np.sin(β), r13/np.sin(β))
print(α)  ## 
print('θ4：',180*α/np.pi + 180)



γ = math.atan2(r32/np.sin(β), -r31/np.sin(β))
print(γ)  ## 
print('θ6：', 180*γ/np.pi + 180)

# β1 = - 180*β/np.pi  

# α1 = 180*α/np.pi + 180  



# γ1 = 180*γ/np.pi + 180
θ3θ2θ1θ5θ4θ6
-2.76035600105476(-158)0.864458274997230(50)1.12251898466603(64)-61°31°-77°❌
-2.76035600105476(-158)0.864458274997230(50)-1.12251898466603(-64)-61°-31°77°❌
-0.616827296276209(-35)-0.864458274997230 (-50)-1.12251898466603(-64)-82°-27°65°
-0.616827296276209(-35)-0.864458274997230(-50)1.12251898466603(64)-82°27-65

❌(-27,-82,65)//(27,-82,-65)

## 通过 R_06  再次验证 
def getR(α, θ):
    α = np.pi * α / 180
    θ = np.pi * θ / 180
    R = [[np.cos(θ), -np.sin(θ), 0],
       [np.sin(θ)*np.cos(α), np.cos(θ)*np.cos(θ), -np.sin(α)],
       [np.sin(θ)*np.sin(α), np.cos(θ)*np.sin(α), np.cos(α)]]
    return R

R_01 = getR(0, -64)
R_12 = getR(-90, 50)
R = np.dot(R_01, R_12)
R_23 = getR(0, -158)
R = np.dot(R, R_23)
R_34 = getR(-90, 33)
R = np.dot(R, R_34)
R_45 = getR(90, 63)
R = np.dot(R, R_45)
R_56 = getR(-90, -29)
R_06 = np.dot(R, R_56)
print(R_06)

# R_06 = [[ -0.8660254,  0. ,0.5],
#         [  0., -1., 0.],
#         [  0.5, 0., 0.8660254]]

Matlab代码_参考

github链接

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/964175.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

酷克数据与华为合作更进一步 携手推出云数仓联合解决方案

酷克数据与华为合作更进一步 携手推出云数仓联合解决方案

在一起，共迎新机遇！8月25-26日，2023华为数据存储用户精英论坛在西宁召开。酷克数据作为国内云原生数据仓库的代表企业，也是华为重要的生态合作伙伴，受邀参与本次论坛，并展示了云数仓领域最新前沿技术以及联…
阅读更多...
微机原理 || 第6章 : I/O接口技术 10道测试题

微机原理 || 第6章 : I/O接口技术 10道测试题

Y2：010 0011，1010B 即003AH
阅读更多...
从半年报里，看中国制造高质量发展的“美的样本”

从半年报里，看中国制造高质量发展的“美的样本”

文 | 螳螂观察 作者 | 图霖 制造业生产和市场需求稳步回升的大背景下，国内制造企业来到新的竞逐拐点，高质量发展的样本企业将获得更大的突围机遇。 作为中国制造代表性企业的美的集团，一直是稳健经营的代表企业。但因受到大环境冲击&#…
阅读更多...
JavaScript设计模式（三）——单例模式、装饰器模式、适配器模式

JavaScript设计模式（三）——单例模式、装饰器模式、适配器模式

个人简介 👀个人主页： 前端杂货铺 🙋‍♂️学习方向： 主攻前端方向，正逐渐往全干发展 📃个人状态： 研发工程师，现效力于中国工业软件事业 🚀人生格言： 积跬步…
阅读更多...
手写RPC框架--2.介绍Zookeeper

手写RPC框架--2.介绍Zookeeper

RPC框架-Gitee代码(麻烦点个Starred, 支持一下吧)https://gitee.com/captaindeng/dcyrpc-framework 该项目的RPC通信将采用NettyZookeeper，所以会在前两章介绍使用方法 介绍Zookeeper Zookeepera.概述1) 数据模型2) Watcher机制 b.安装和基本操作1) Java操作zookeep…
阅读更多...
记一次postgres导致cpu100%

记一次postgres导致cpu100%

周末想打两把训练赛，没想到朋友发来一个截图 我：嗯？？wtf 于是我上服务器看了一下日志，诶我超，还真的 查看进程详情 [rootiZ7xv7q4im4c48qen2do2bZ project]# pstree -tp postgres memory(904475)─┬─…
阅读更多...
分布式锁实现二. memcached分布式锁

分布式锁实现二. memcached分布式锁

文章目录 memcached分布式锁实现原理：优缺点 开发准备安装memcached服务端安装jar到maven本地仓库 代码开发初始化Memcached客户端锁相关操作核心代码本地运行效果docker运行效果 memcached分布式锁 实现原理： memcached带有add函数，利用ad…
阅读更多...
【半监督医学图像分割】2022-MedIA-UWI

【半监督医学图像分割】2022-MedIA-UWI

【半监督医学图像分割】2022-MedIA-UWI 论文题目：Semi-supervise d me dical image segmentation via a triple d-uncertainty guided mean teacher model with contrastive learning 中文题目：基于对比学习的三维不确定性指导平均教师模型的半监督图像分…
阅读更多...
Linux编程--进程--fork使用，创建父子进程

Linux编程--进程--fork使用，创建父子进程

1.使用fork函数创建一个进程 #include <unistd.h>pid_t fork(void); 返回值为0&#xff0c;代表当前进程是子进程 返回值为非负数&#xff0c;代表当前进程为父进程 调用失败&#xff0c;返回-1 代码&#xff1a; #include <stdio.h> #include <sys/types.h&g…
阅读更多...
锁（ ReentrantLock，Synchronized）

锁（ ReentrantLock，Synchronized）

1.lock和synchronized 语法层面 synchronized 是关键字&#xff0c;源码在 jvm 中&#xff0c;用 c 语言实现&#xff1b; Lock 是接口&#xff0c;源码由 jdk 提供&#xff0c;用 java 语言实现&#xff1b; 使用 synchronized 时&#xff0c;退出同步代码块锁会自动释放&…
阅读更多...
idea中设置指定图片为项目站标

idea中设置指定图片为项目站标

前提是准备好一张图片 在idea中创建imgs文件夹&#xff0c;放入图片 创建一个HTML文件 建立链接link标签&#xff0c;链接照片即可 <link href"../02css/imgs/2.jpg" rel"shortcut icon" type"image/x-icon"> 执行效果如下图所示&…
阅读更多...
音频——I2S 左对齐模式(三)

音频——I2S 左对齐模式(三)

I2S 基本概念飞利浦(I2S)标准模式左(MSB)对齐标准模式右(LSB)对齐标准模式DSP 模式TDM 模式 文章目录 I2S left波形图逻辑分析仪抓包 I2S left I2S 左对齐标准 标准左对齐格式的数据的 MSB 没有相对于 BCLK 延迟一个时钟。左对齐格式的左右声道数据的 MSB 在 LRCLK 边沿变化后…
阅读更多...
斐波那契数【动态规划】

斐波那契数【动态规划】

斐波那契数 斐波那契数 &#xff08;通常用 F(n) 表示&#xff09;形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始&#xff0c;后面的每一项数字都是前面两项数字的和。也就是&#xff1a; F(0) 0&#xff0c;F(1) 1 F(n) F(n - 1) F(n - 2)&#xff0c;其中 n >…
阅读更多...
Golang：微服务常用代码分层结构

Golang：微服务常用代码分层结构

1.代码结构 代码分层结构是一个老生常谈的话题&#xff0c;好的代码结构能够使得系统易于理解、开发及维护&#xff0c;如果代码结构很混乱就会使得不同层级的代码块耦合&#xff0c;导致难以维护和拓展。 比较经典的代码结构&#xff08;宏观&#xff09;有Web的MVC模式分层结…
阅读更多...
SpringBoot整合websockt实现消息对话

SpringBoot整合websockt实现消息对话

文章目录 前言websockt什么是websockt&#xff1f;websockt和Socket区别代码部分实战应用 前言 websockt 什么是websockt&#xff1f; WebSocket是一种在Web应用程序中实现实时双向通信的技术。Web应用程序通常是基于HTTP协议的&#xff0c;HTTP是一种请求/响应式的协议&…
阅读更多...
【服务器使用基础】---华为云云耀云服务器实例使用实践

【服务器使用基础】---华为云云耀云服务器实例使用实践

&#x1f996;我是Sam9029&#xff0c;一个前端 Sam9029的CSDN博客主页:Sam9029的博客_CSDN博客-JS学习,CSS学习,Vue-2领域博主 **&#x1f431;‍&#x1f409;&#x1f431;‍&#x1f409;恭喜你&#xff0c;若此文你认为写的不错&#xff0c;不要吝啬你的赞扬&#xff0c;求…
阅读更多...
肖sir__linux详解__003（vim命令）

肖sir__linux详解__003（vim命令）

linux 文本编辑命令 作用&#xff1a;用于编辑一个文件 用法&#xff1a;vim 文件名称 或者vi &#xff08;1&#xff09;编辑一个存在的文档 例子&#xff1a;编辑一个file1文件 vim aa &#xff08;2&#xff09;编辑一个文件不存在&#xff0c;会先创建文件&#xff0c;再…
阅读更多...
Python-图像拼接神器-stitching

Python-图像拼接神器-stitching

多幅图像的拼接 采用这个包&#xff0c;图像拼接结果很好~ 代码只需要三四行 import stitching import cv2imgs ["data/test02/1Hill.jpg","data/test02/2Hill.jpg","data/test02/3Hill.jpg",] stitcher stitching.Stitcher() panorma stit…
阅读更多...
postgresql-多表连接

postgresql-多表连接

postgresql-多表连接 内连接查询左外连接查询右外连接查询全外连接查询交叉连接查询简写 总结 内连接查询 内连接用于返回两个表中匹配的数据行&#xff0c;使用关键字INNER JOIN表示&#xff0c;也可以简写成JOIN&#xff1b; selecte.first_name ,d.department_id fromcps…
阅读更多...
无涯教程-JavaScript - POISSON函数

无涯教程-JavaScript - POISSON函数

POISSON函数取代了Excel 2010中的POISSON.DIST函数。 描述 该函数返回泊松分布。泊松分布的常见应用是预测特定时间的事件数。 语法 POISSON(x,mean,cumulative)争论 Argument描述Required/OptionalXThe number of events.RequiredMeanThe expected numeric value.Require…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023