文章目录

- C 环境准备
- - 官方文档
  - 环境准备
  - - 在线运行
    - VSCode
  - 环境报错解决
- 绪论
- 线性表
- - 顺序表
  - 链表
  - 错题
- 栈、队列和数组
- - 栈
  - 队列
  - 栈的应用之中缀转后缀
  - 特殊矩阵用数组压缩存储
  - 错题
- 串
- - 模式匹配之暴力和KMP
- 树与二叉树
- - 二叉树
  - 树和森林
  - 哈夫曼树和哈夫曼编码
  - 并查集
  - 错题
- 图
- - 图的基本概念
  - 图的存储及基本操作
  - 图的遍历
  - 图的应用
  - 错题
- 查找
- - 顺序查找
  - 二分查找
  - 分块查找
  - 树型查找
  - B树和B+树
  - 散列表
  - 错题
- 排序
- - 错题
- C++相关零碎知识点
参考资料

C 环境准备

官方文档

ISO/IEC
The GNU C Reference Manual
cppreference.com

环境准备

在线运行

菜鸟教程在线运行

VSCode

安装两个插件，C/C++（必须安装）和 Code Runner，编写C示例程序，运行即可

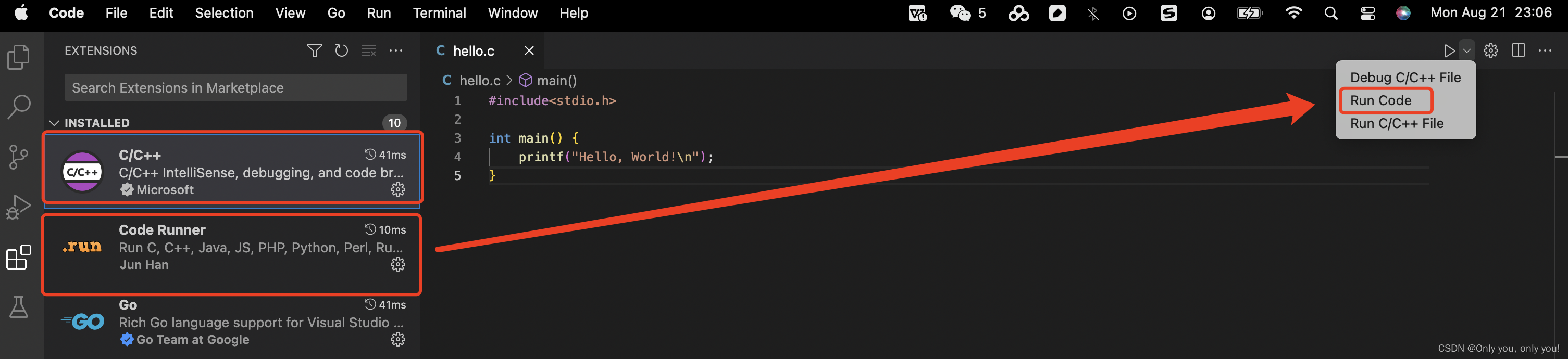
在这里插入图片描述

也可这么编译、运行（初次运行，选择 mac 自带的 clang 编译器）

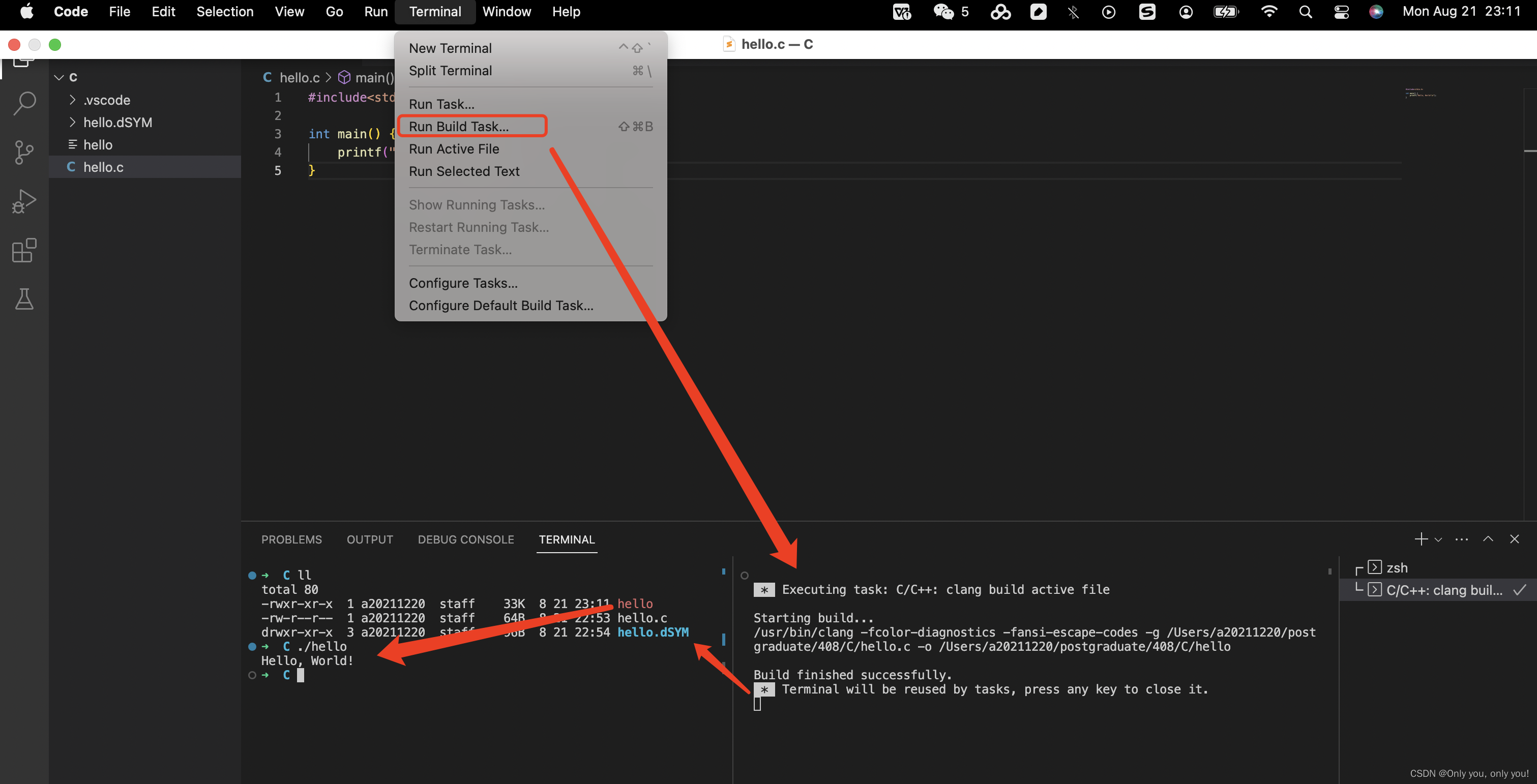
在这里插入图片描述

查看编译器支持的 C/C++ 版本（VSCode 可用 command + 逗号，输入 C_Cpp.default.cp，C_Cpp.default.cp）

printf("%ld\n",__STDC_VERSION__);

printf("%ld\n",__cplusplus);

环境报错解决

报错：Undefined symbols for architecture arm64
解决：删除非代码文件的其他文件/目录，选用 C/C++: clang++ build active file 重新编译

绪论

线性表

顺序表

#include<cstdio>
#include<cstdlib>

// ----- 2.2.1 顺序表的定义 ----- 

// 为方便写代码，不爆红，不妨如此定义一下
typedef int ElementType;

// 静态分配
#define MaxSize 50
typedef struct {
    ElementType data[MaxSize];
    int length;
} SqList;

// 动态分配
#define InitSize 100
typedef struct {
    ElementType *data;
    int length;
} SqList;
// 动态分配实现
// L.data = (ElementType *)malloc(sizeof(ElementType) * InitSize);


// ----- 2.2.2 顺序表基本操作 ----- 

// 插入，第 i 位置（线性表位序从 1 开始）插入 e
bool ListInsert(SqList &L, int i, ElementType e) {
    if(L.length >= MaxSize) {
        return false;
    }
    // 插入位置合法范围是 [1, L.length + 1]
    if(i < 1 || i > L.length + 1) {
        return false;
    }
    for(int j = L.length; j >= i; j--) {
        L.data[j] = L.data[j - 1];
    }
    L.data[i - 1] = e;
    L.length++;
    return true;
}

// 删除，删除第 i 个元素
bool ListDelete(SqList &L, int i, ElementType &e) {
    if(i < 1 || i > L.length) {
        return false;
    }
    e = L.data[i - 1];
    for(int j = i; j < L.length; j++) {
        L.data[j - 1] = L.data[j];
    }
    L.length--;
    return true;
}
 
// 查找
int LocateElem(SqList &L, ElementType e) {
    for(int i = 0; i < L.length; i++) {
        if(L.data[i] == e) {
            return i + 1;
        }
    }
    return 0;
}

// ----- 历年真题 ----- 

/*
    2010，一维数组循环左移
    
    例子，abcdefgh 循环左移 3 位，得到 defghabc
    算法，1) abc 逆置得到 cbadefgh；2) defgh 再逆置得到 cbahgfed；3) 整体逆置得到 defghabc
    tip，统考题目写出可行解法就可得到大部分分数，不必耗费心思写出最优解！
*/
void Swap(int a[], int i, int j) {
    int t = a[i];
    a[i] = a[j];
    a[j] = t;
}
void Reverse(int R[], int from, int to) {
    int len = to - from + 1;
    for(int i = 0; i < len / 2; i++) {
        Swap(R, i + from, to - i);    // len - 1 - i + from = to - i
    }
}
void Converse(int R[], int n, int p) {
    Reverse(R, 0, p - 1);
    Reverse(R, p, n - 1);
    Reverse(R, 0, n - 1);
}

链表

#include<cstdio>
#include<cstdlib>

// 为方便写代码，不爆红，不妨如此定义一下
typedef int ElementType;

// ----- 2.3.1 单链表的定义 -----

typedef struct LNode{
    ElementType data;
    struct LNode *next;
} LNode, *LinkList;
// （可选）头结点：第一个结点之前附加一个结点。


// ----- 2.3.2 单链表基本操作 -----

// 创建单链表，头插法
LinkList ListCreateHeadInsert(LinkList L) {
    int x;
    scanf("%d", &x);
    while(x != 9999) {  // 9999 表示停止输入
        LNode *node = (LNode *)malloc(sizeof(LNode));
        node->data = x;
        node->next = L->next;
        L->next = node;
        scanf("%d", &x);
    }
    return L;
}

// 创建单链表，尾插法
LinkList ListCreateTailInsert(LinkList L) {
    int x;
    LNode * tail = L;
    scanf("%d", &x);
    while(x != 9999) {  // 9999 表示停止输入
        LNode *node = (LNode *)malloc(sizeof(LNode));
        node->data = x;
        node->next = NULL;
        tail->next = node;
        tail = node;
        scanf("%d", &x);
    }
    return L;
}

// 按序号查找结点
LNode *ListGetElem(LinkList L, int i) {
    if(i < 0) {
        return NULL;
    }
    if(i == 0) {
        return L;
    }
    LNode *p = L->next;
    int j = 1;
    while(j < i && p) { // 若 i 大于表长，最终会返回 NULL
        p = p->next;
        j++;
    }
    return p;
}

// 按值查找结点
LNode *ListGetElem(LinkList L, ElementType e) {
    LNode *p = L->next;
    while(p && p->data != e) {  // 找不到 e 就返回 NULL
        p = p->next;
    }
    return p;
}

// 插入，在第 i 个位置
bool ListInsert(LinkList L, int i, LNode *node) {
    LNode *pre = ListGetElem(L, i - 1);
    if(pre == NULL) {
        return false;
    }
    node->next = pre->next;
    pre->next = node;
    return true;
}

// 插入，在指定结点后插。如果前插，需要先找前驱结点，而比较 tricky 的办法是后插并交换结点值！
void ListInsert(LinkList L, LNode *node, LNode *specify) {
    node->next = specify->next;
    specify->next = node;
}

// 删除，第 i 个位置。如果删除指定结点，需要先找前驱结点，而比较 tricky 的办法是把后继结点的值赋予待删结点并删除后继结点，然而后继结点若是 NULL，此办法也不可行！
bool ListDelete(LinkList L, int i) {
    LNode *pre = ListGetElem(L, i - 1);
    if(pre == NULL) {
        return false;
    }
    LNode *deleteNode = pre->next;
    pre->next = deleteNode->next;
    free(deleteNode);
    return true;
}

// 表长
int ListLength(LinkList L) {
    int length = 0;
    LNode *p = L;
    while(p->next != NULL) {
        length++;
        p = p->next;
    }
    return length;
}


// ----- 2.3.3 双链表 -----

// 双链表结点类型描述
typedef struct DNode {
    ElementType data;
    struct DNode *pre, *next;
} DNode, *DLinkList;

// 双链表插入
void DListInsert(DNode *node, DNode *specify) {
    node->next = specify->next;
    specify->next->pre = node;
    node->pre = specify;
    specify->next = node;
}

// 双链表删除
void DListDelete(DNode *node) {
    node->pre->next = node->next;
    node->next->pre = node->pre;
    free(node);
}


// ----- 2.3.4 循环链表 -----

// 循环单链表，尾结点的 next 指向 L，注意删除、插入、判空相较于单链表的特殊处理
// 循环双链表，尾结点的 next 指向 L，头结点的 pre 指向 尾结点


// ----- 2.3.5 静态链表 -----

// 静态链表利用数组实现链式存储结构
#define MaxSize 100
typedef struct {
    ElementType data;
    int next;   // 指向数组索引，以 -1 作为终止标志
} SLinkList[MaxSize];


// ----- 2.3.6 顺序表和链表比较 -----

// 顺序表删除平均移动半个表长数据，而单链表虽说也要查找前驱，但只是查找（比较操作），不需移动操作，效率更优

错题

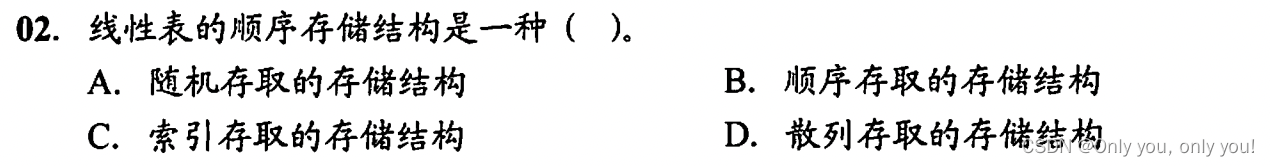
在这里插入图片描述

答案：A

在这里插入图片描述

答案：D（注意是第 i 个元素，双向链表也得从头开始走到第 i 个节点）

在这里插入图片描述

答案：C

在这里插入图片描述

答案：D

栈、队列和数组

栈


// 为方便写代码，不爆红，不妨如此定义一下
typedef int ElementType;

// ----- 3.1.2 栈的顺序存储结构 -----

#define MaxSize 100

typedef struct {
    ElementType data[MaxSize];
    int top;
} SqStack;

// 初始化
void Init(SqStack &s) {
    s.top = -1;
}

// 判栈空
bool Empty(SqStack &s) {
    return s.top == -1;
} 

// 判栈满
bool Full(SqStack &s) {
    return s.top + 1 == MaxSize;
}

// 栈长度
int Length(SqStack &s) {
    return s.top + 1;
}

// 进栈
bool Push(SqStack &s, ElementType e) {
    if(Full(s)) {
        return false;
    }
    s.data[++s.top] = e;
    return true;
}

// 出栈
bool Pop(SqStack &s, ElementType &e) {
    if(Empty(s)) {
        return false;
    }
    e = s.data[s.top--];
    return true;
}

// 读取栈顶元素
bool Top(SqStack &s, ElementType &e) {
    if(Empty(s)) {
        return false;
    }
    e = s.data[s.top];
    return true;
}

// 共享栈，两个顺序栈共用一个一维数组，两栈底分别在数组两端，两栈顶相邻时，共享栈满


// ----- 3.1.3 栈的链式存储结构 -----
typedef struct LinkNode {
    ElementType data;
    struct LinkNode *next;
} *LinkStack;

队列

#include<cstdlib>

// 为方便写代码，不爆红，不妨如此定义一下
typedef int ElementType;

// ----- 3.2.2 队列的顺序存储结构 -----

#define MaxSize 100

// 队空：front = tail = 0；入队：data[tail++]；出队：data[front++]；
typedef struct {
    ElementType data[MaxSize];
    int front, tail;
} SqQueue;

// 循环队列
void InitCircularQ(SqQueue &Q) {
    Q.front = Q.tail = 0;
}

// 循环队列判空
bool CircularQEmpty(SqQueue &Q) {
    return Q.front == Q.tail;
}

// 循环队列判满，牺牲一个单元判队满
bool CircularQFull(SqQueue &Q) {
    return (Q.tail + 1) % MaxSize == Q.front;
}

// 循环队列入队
bool CircularQIn(SqQueue &Q, ElementType e) {
    if(CircularQFull(Q)) {
        return false;
    }
    Q.data[Q.tail] = e;
    Q.tail = (Q.tail + 1) % MaxSize;
    return true;
}

// 循环队列出队
bool CircularQOut(SqQueue &Q, ElementType &e) {
    if(CircularQEmpty(Q)) {
        return false;
    }
    e = Q.data[Q.front];
    Q.front = (Q.front + 1) % MaxSize;
    return true;
}


// ----- 3.2.3 队列的链式存储结构 -----

typedef struct LinkNode{
    ElementType data;
    struct LinkNode *next;
} LinkNode;
typedef struct {
    LinkNode *front, *tail;
} LinkQueue;

// 初始化，使用含头结点的链表方式实现
void Init(LinkQueue &Q) {
    Q.front = Q.tail = (LinkNode *)malloc(sizeof(LinkNode));
    Q.front = NULL;
}

// 判空
bool Empty(LinkQueue &Q) {
    return Q.front == Q.tail;
}

// 入队
void Push(LinkQueue &Q, ElementType e) {
    LinkNode *node = (LinkNode *)malloc(sizeof(LinkNode));
    node->next = NULL;
    node->data = e;
    Q.tail->next = node;
    Q.tail = node;
}

// 出队
bool Pop(LinkQueue &Q, ElementType &e) {
    if(Empty(Q)) {
        return false;
    }
    LinkNode *p = Q.front->next;
    e = p->data;
    Q.front->next = p->next;
    if(Q.tail == p) {
        Q.tail = Q.front;
    }
    free(p);
    return true;
}

栈的应用之中缀转后缀

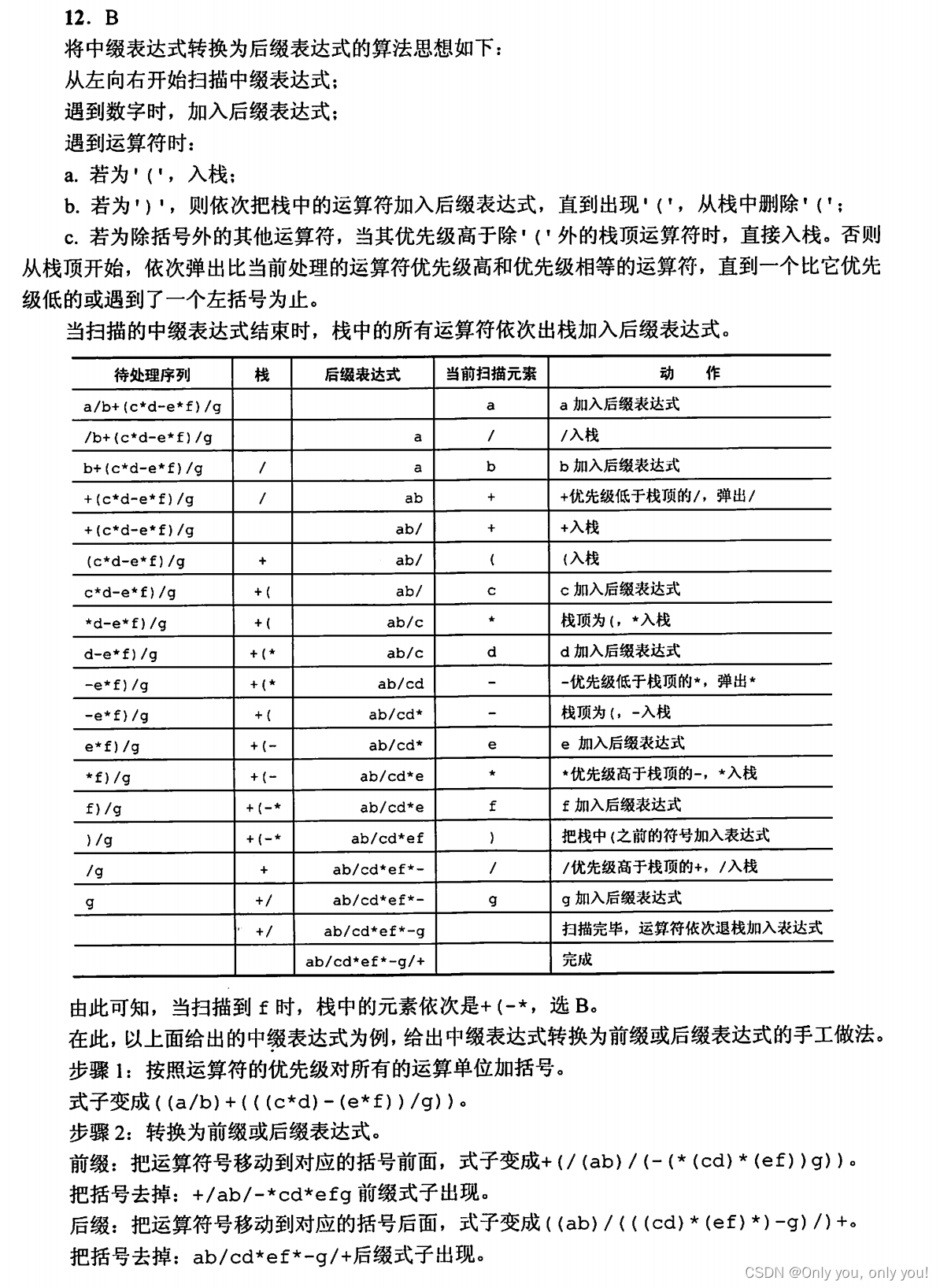
在这里插入图片描述

特殊矩阵用数组压缩存储

在这里插入图片描述

答案：A（注意了解对称矩阵、三角矩阵和三对角矩阵的概念，以及按列或行优先存储成压缩数组的含义）

错题

在这里插入图片描述

答案：B(都是线性结构)

在这里插入图片描述

答案：C（头插）

在这里插入图片描述

答案：D

在这里插入图片描述

答案：C（后面的 3 都没出来呢，你这个 4 咋可能先出来呢！）

在这里插入图片描述

答案：D（数组长度是 n + 1）

在这里插入图片描述

答案：D

在这里插入图片描述

答案：C（注意双端队列进出顺序，比如全左进 1 2 3 4，全左出 4 3 2 1）

在这里插入图片描述

答案：B（题意是插入 A[0] 后，front = rear = 0）

串

模式匹配之暴力和KMP

#include<cstdio>
#include<string>
#include<iostream>

using namespace std;

int indexOf(string s1, string s2);
int kmp(string s1, string s2);

int main() {
    string s1 = "abccabc";
    string s2 = "cab";
    
    int loc = s1.find(s2);
    printf("%d\n", loc);

    loc = indexOf(s1, s2);
    printf("%d\n", loc);

    loc = kmp(s1, s2);
    printf("%d\n", loc);
   
}

int indexOf(string s1, string s2) {
    for(int i = 0; i < s1.length(); i++) {
        int j = 0, k = i;
        while (j < s2.length() && k < s1.length() && s1[k] == s2[j]) {
            j++;
            k++;
        }
        if(j == s2.length()) {
            return i;
        }
        
    }
    return -1;
}

/**
 * next 数组求解
 * 
 * 例子，s = "ABABC"
 * next[0] = 0，前 1 个字符 "A" 最长相同前后缀长度是 0
 * next[1] = 0，前 2 个字符 "AB" 最长相同前后缀长度是 0
 * next[2] = 1，前 3 个字符 "ABA" 最长相同前后缀是 "A"，长度是 1
 * next[3] = 2，前 4 个字符 "ABAB" 最长相同前后缀是 "AB"，长度是 2
 * next[4] = 0，前 5 个字符 "ABABC" 最长形态前后缀长度是 0
 * 
*/
int * buildNext(string s) {
    int *next = (int *)malloc(sizeof(int) * s.length());
    next[0] = 0;
    int commonPrefixSuffixLen = 0;
    int i = 1;
    while(i < s.length()) {
        if(s[commonPrefixSuffixLen] == s[i]) {
            commonPrefixSuffixLen++;
            next[i] = commonPrefixSuffixLen;
            i++;
        } else {
            if(commonPrefixSuffixLen == 0) { // 当前字符跟首字符不同，next[i] 必定是 0
                next[i] = 0;
                i++;
            } else {    // 迭代
                commonPrefixSuffixLen = next[commonPrefixSuffixLen - 1];
            }
        }
    }
    return next;
}

/**
 * kmp 算法，主串 s1，子串 s2
 * 
 * 例子，
 * 主串：ABABABCAA
 * 子串：ABABC
 * 
 * 首次不匹配的是主串的 A 和子串的 C，此时后移变为：
 * 主串：ABABABCAA
 * 子串：  ABABC
 * 
*/
int kmp(string s1, string s2) {
    int *next = buildNext(s2);
    int i = 0, j = 0;
    while(i < s1.length()) {
        if(s1[i] == s2[j]) {
            i++;
            j++;
        } else if(j > 0) {
            j = next[j - 1];
        } else {    // 子串第一个字符就失配
            i++;
        }

        if(j == s2.length()) {
            return i - j;
        }
    }
    return -1;
}

树与二叉树

二叉树

#include<cstdio>
#include<stack>
#include<queue>

using namespace std;

// 为方便写代码，不爆红，不妨如此定义一下
typedef int ElementType;

// ----- 5.2.1 二叉树的定义及其主要特性 -----

/**
 * 二叉树的性质
 * 1. 非空二叉树的叶结点数等于度为 2 的结点数加 1。
 *    推导依据，树的分叉数加 1 等于结点数，n = n0 + n1 + n2 = n0 * 0 + n1 * 1 + n2 * 2 + 1，得到 n0 = n2 + 1。
 * 
 * 2. 非空二叉树有 n + 1 个空指针。
 *    推导依据，每个度为 0 和 1 的结点分别有 2 个和 1 个空指针，则空指针总数是 n0 * 2 + n1 * 1，又 n0 = n2 + 1，可求得空指针总数是 n + 1。
*/


// ----- 5.2.2 二叉树的存储结构 -----

// 顺序存储，适合满二叉树和完全二叉树，否则要用 0 填充很多不存在的空结点

// 链式存储。重要结论：含有 n 个结点的二叉链表中，有 n + 1 个空链域
typedef struct BiTNode {
    ElementType data;
    struct BiTNode *lChild, *rChild;
} BiTNode, *BiTree;

// ----- 5.3.1 二叉树的遍历 -----

void Visit(BiTNode *node) {}

// 先序遍历
void PreOrder(BiTree T) {
    if(T != NULL) {
        Visit(T);
        PreOrder(T->lChild);
        PreOrder(T->rChild);
    }
}

// 中序遍历
void InOrder(BiTree T) {
    if(T != NULL) {
        InOrder(T->lChild);
        Visit(T);
        InOrder(T->rChild);
    }
}

// 后序遍历
void PostOrder(BiTree T) {
    if(T != NULL) {
        PostOrder(T->lChild);
        PostOrder(T->rChild);
        Visit(T);
    }
}

// 先序遍历，非递归
void PreOrderStack(BiTree T) {
    BiTNode *p = T;
    stack<BiTree> s;
    while(p || !s.empty()) {
        if(p) {
            Visit(p);
            s.push(p);
            p = p->lChild;
        } else {
            p = s.top();
            s.pop();
            p = p->rChild;
        }
    }
}

// 中序遍历，非递归
void InOrderStack(BiTree T) {
    BiTNode *p = T;
    stack<BiTree> s;
    while(p || !s.empty()) {
        if(p) {
            s.push(p);
            p = p->lChild;
        } else {
            p = s.top();
            s.pop();
            Visit(p);
            p = p->rChild;
        }
    }
}

// 后序遍历，非递归，按根右左顺序入栈，最后总出栈时就是左右根的顺序，即后序遍历
void PostOrderStack(BiTree T) {
    stack<BiTree> s1;
    stack<BiTree> s2;

    BiTNode *p = T;
    s1.push(p);
    while(!s1.empty()) {
        p = s1.top();
        s1.pop();
        s2.push(p);
        if(p->lChild != NULL) {
            s1.push(p->lChild);
        }
        if(p->rChild != NULL) {
            s1.push(p->rChild);
        }
    }
    while (!s2.empty()) {
        p = s2.top();
        s2.pop();
        Visit(p);
    }
}

// 层次遍历
void LevelOrder(BiTree T) {
    queue<BiTree> q;
    BiTNode *p = T;
    q.push(p);
    while (!q.empty()) {
        p = q.front();
        q.pop();
        Visit(p);
        if(p->lChild != NULL) {
            q.push(p->lChild);
        }
        if(p->rChild != NULL) {
            q.push(p->rChild);
        }
    }
}


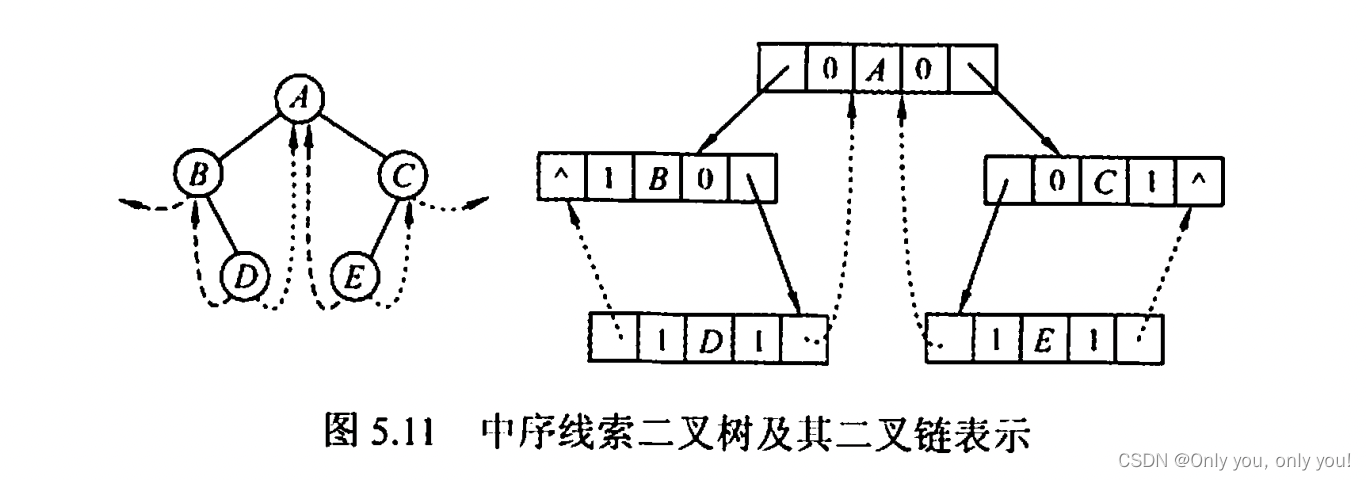
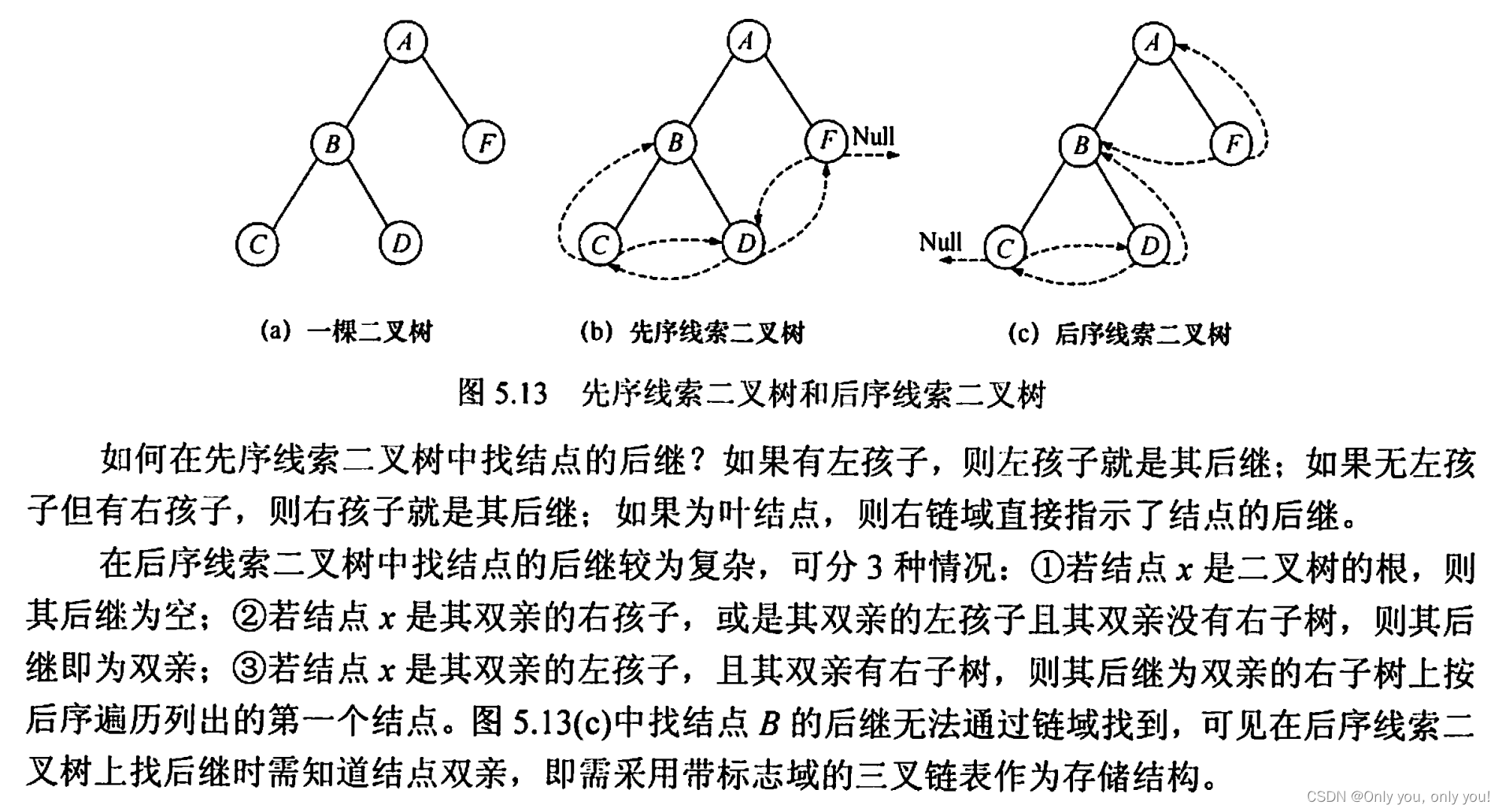
// ----- 5.3.2 线索二叉树 -----

// 线索二叉树方便得到二叉树结点的前驱和后继

typedef struct ClueBiTNode {
    ElementType data;
    struct ClueBiTNode *lChild, *rChild;
    // lTag = 0，lChild 指向左孩子；lChild = 1，lChild 指向前驱
    // rTag = 0，rChild 指向右孩子；rChild = 1，rChild 指向后继
    int lTag, rTag;
} ClueBiTNode, *ClueBiTree;

// 中序遍历对二叉树线索化
void ClueBiTreeIn(ClueBiTree p, ClueBiTNode *pre) {
    if(p != NULL) {
        ClueBiTreeIn(p->lChild, pre);
        if(p->lChild == NULL) {
            p->lChild = pre;
            p->lTag = 1;
        }
        if(pre != NULL && pre->rChild == NULL) {
            pre->rChild = p;
            pre->rTag = 1;
        }
        pre = p;
        ClueBiTreeIn(p->rChild, pre);
    }    
}
// 中序遍历建立线索二叉树
void CreateClueBiTreeIn(ClueBiTree T) {
    ClueBiTNode *pre = NULL;
    if(T != NULL) {
        ClueBiTreeIn(T, pre);
        pre->rChild = NULL; // 最后一个结点的后继置为 NULL
        pre->rTag = 1;
    }
}

// 中序线索二叉树中序序列以 T 为树根的第一个结点
ClueBiTNode * ClueBiTFirstNodeIn(ClueBiTree T) {
    ClueBiTNode *p = T;
    while(p->lTag == 0) {
        p = p->lChild;
    }
    return p;
}

// 中序线索二叉树中序序列结点 p 的后继
ClueBiTNode * ClueBiTNextNodeIn(ClueBiTNode *p) {
    if(p->rTag == 1) {
        return p->rChild;
    }
    return ClueBiTFirstNodeIn(p->rChild);
}

// 中序线索二叉树的中序遍历
void ClueBiIn(ClueBiTree T) {
    for(ClueBiTNode *p = ClueBiTFirstNodeIn(T); p != NULL; p = ClueBiTNextNodeIn(p)) {
        // 操作当前遍历到的结点 p
    }
}

线索二叉树
在这里插入图片描述

在这里插入图片描述

树和森林

树转成二叉树
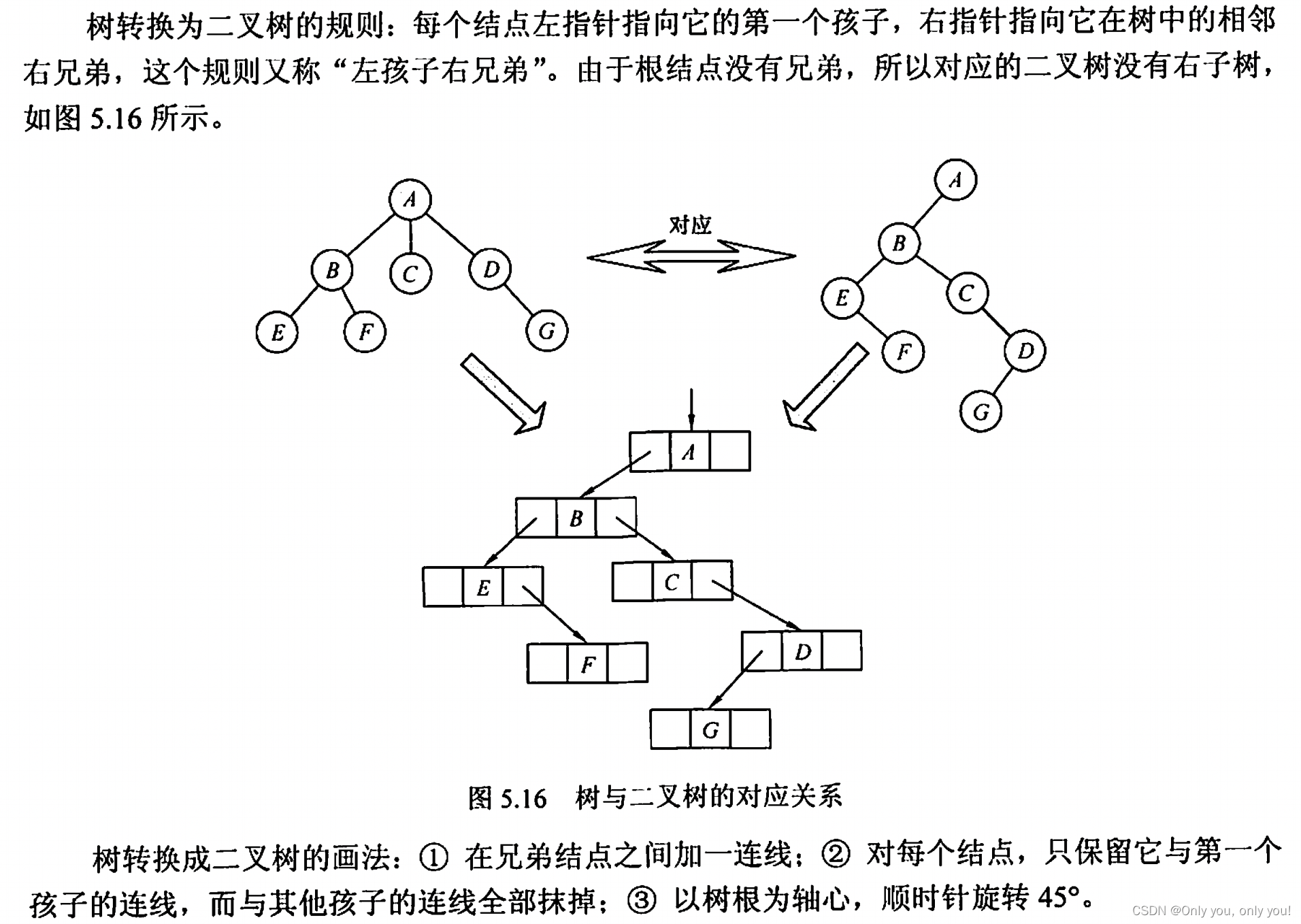
在这里插入图片描述
5.16 树的先根遍历：ABEFCDG，后根遍历（对应二叉树的中序遍历）：EFBCGDA

森林和二叉树互转

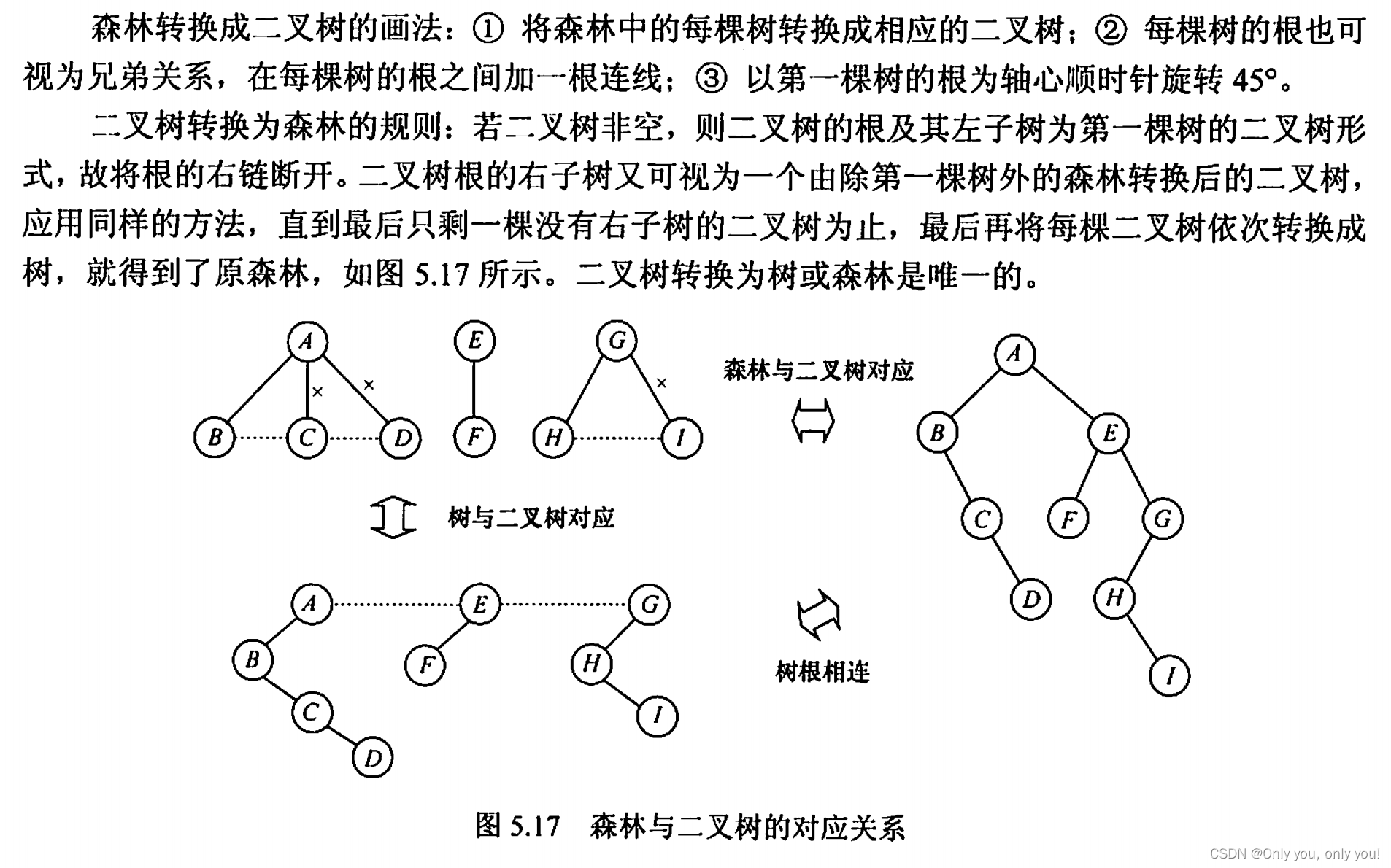
在这里插入图片描述
5.17 森林的先序遍历：ABCDEFGHI，中序遍历：BCDAFEHIG。要是不明白的话，就把他转成二叉树再遍历。

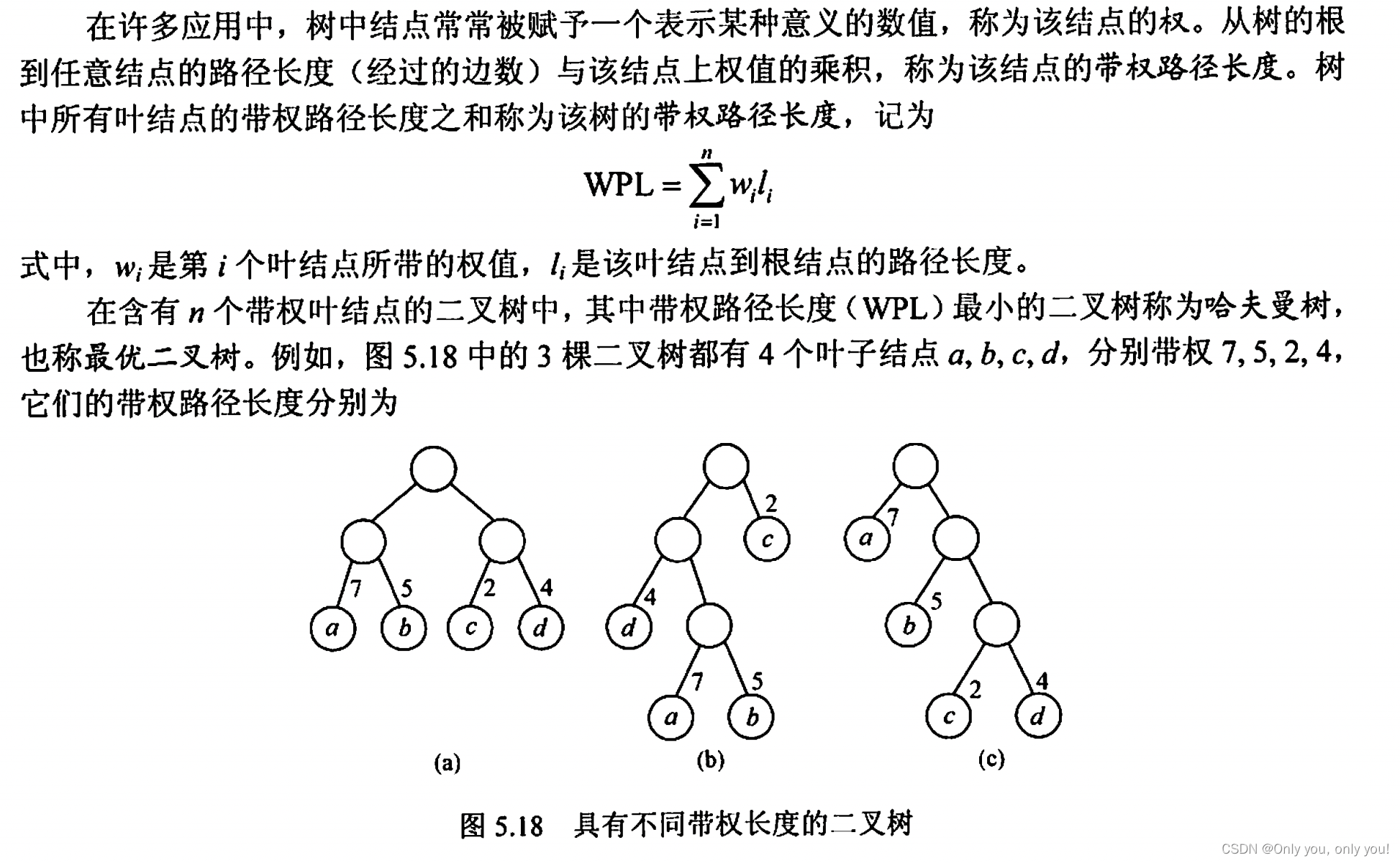
哈夫曼树和哈夫曼编码

哈夫曼树
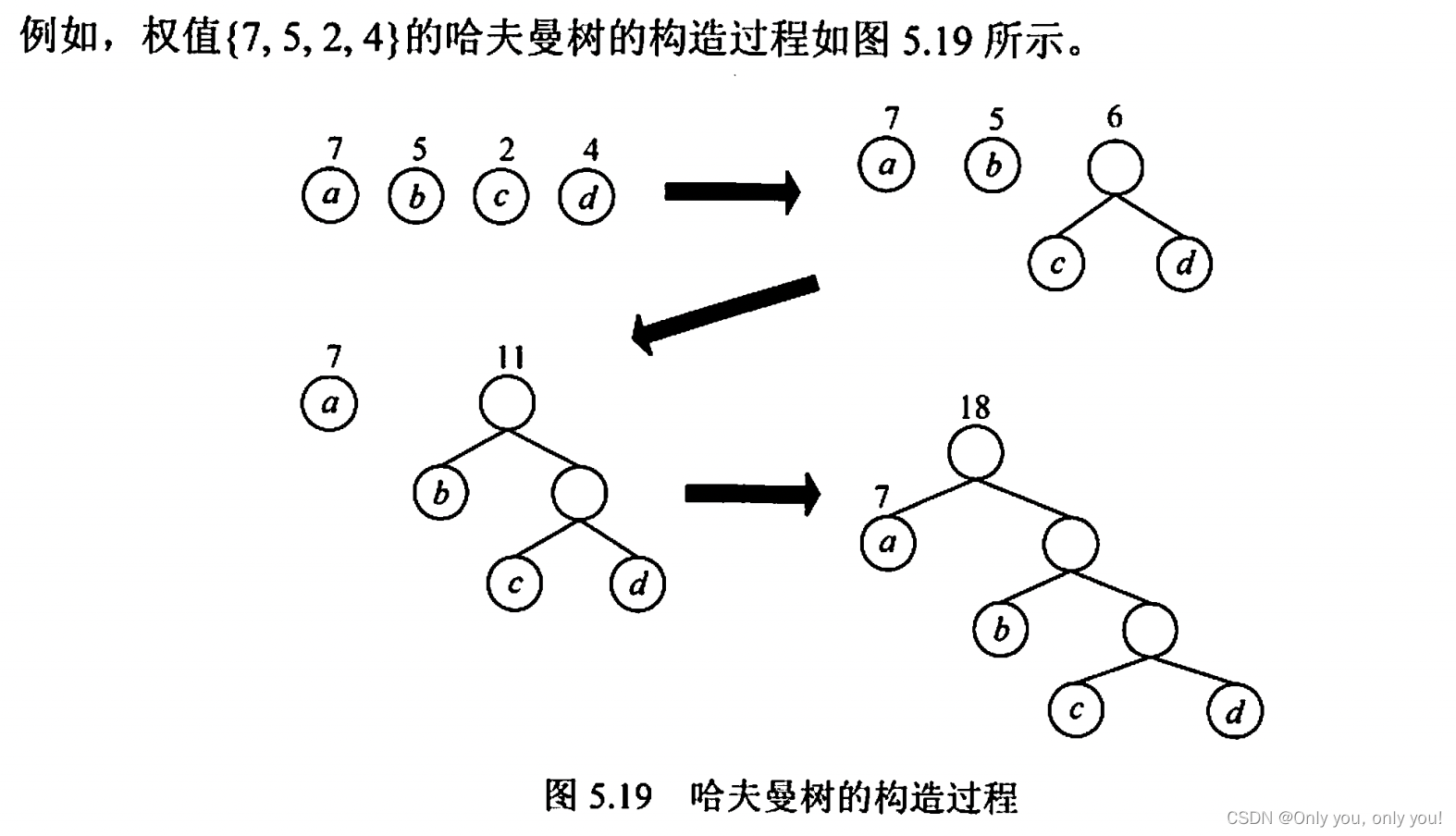
在这里插入图片描述

哈夫曼编码

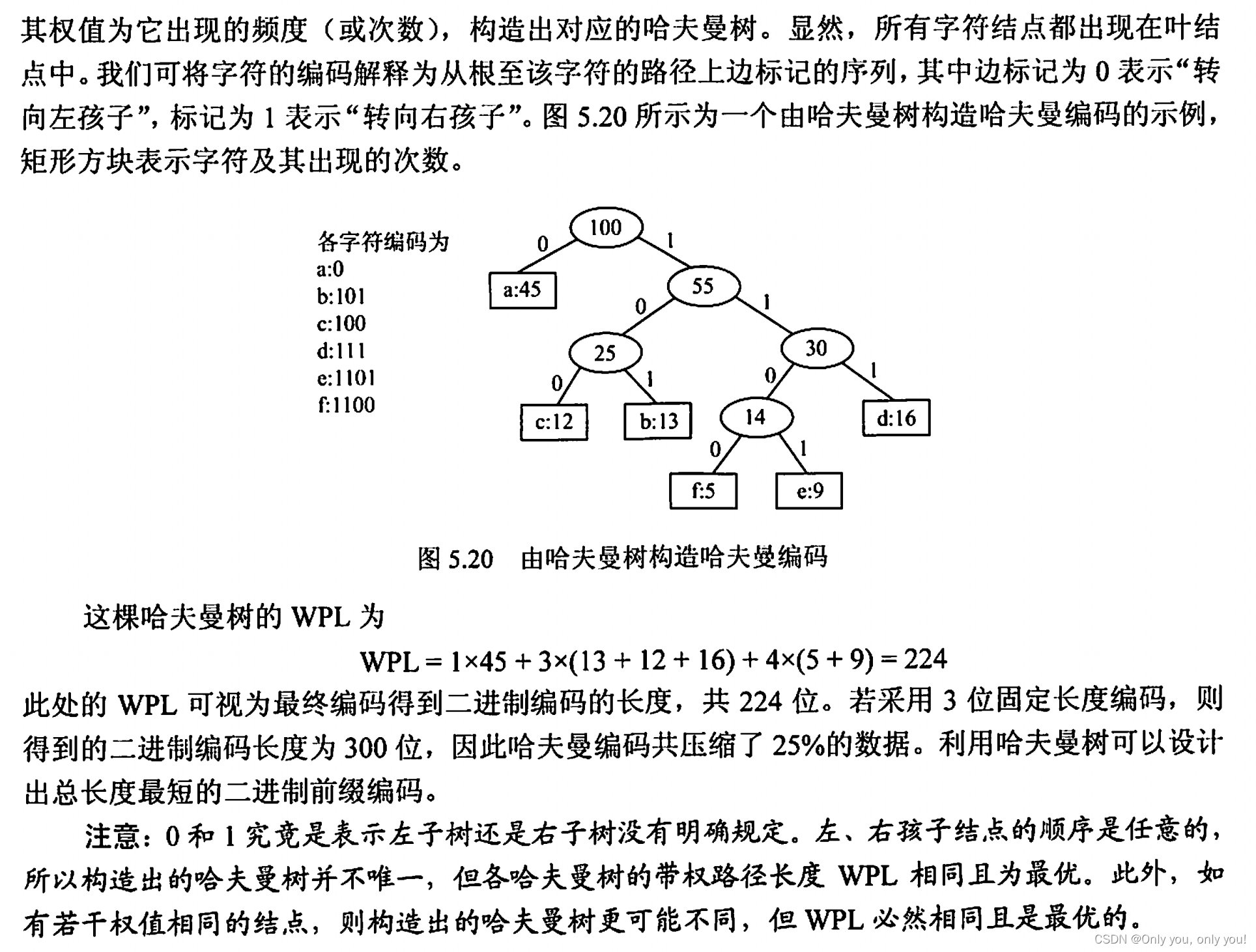
在这里插入图片描述

并查集

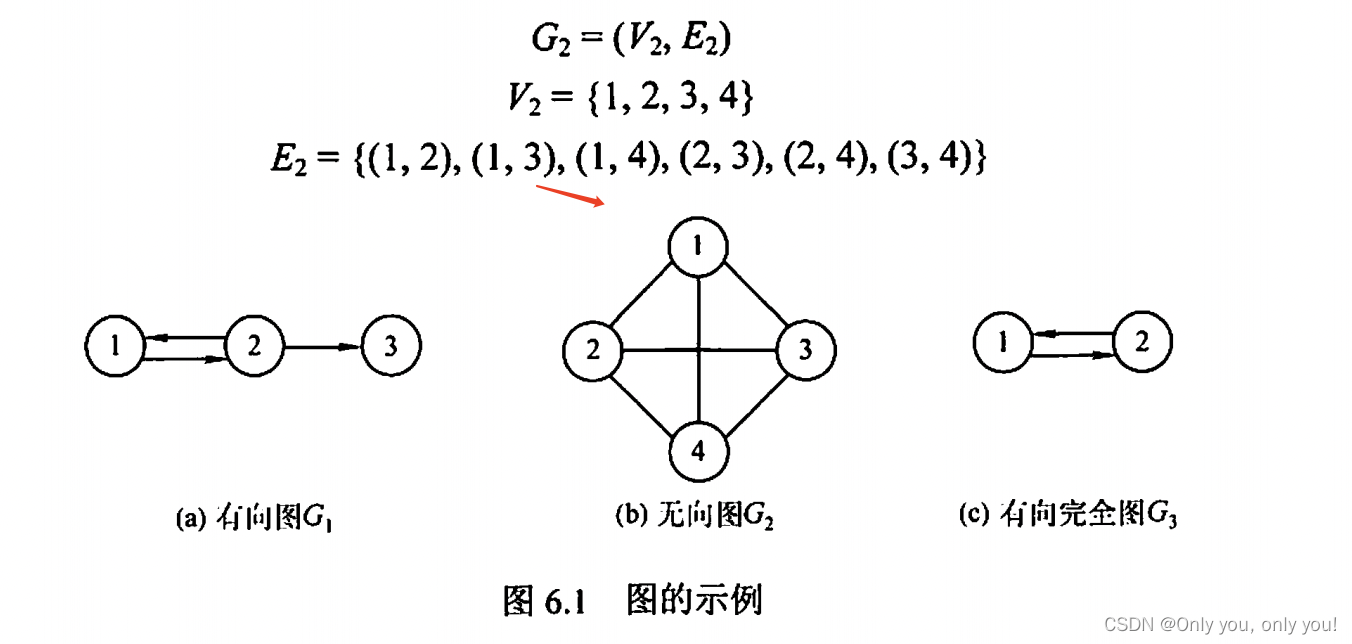
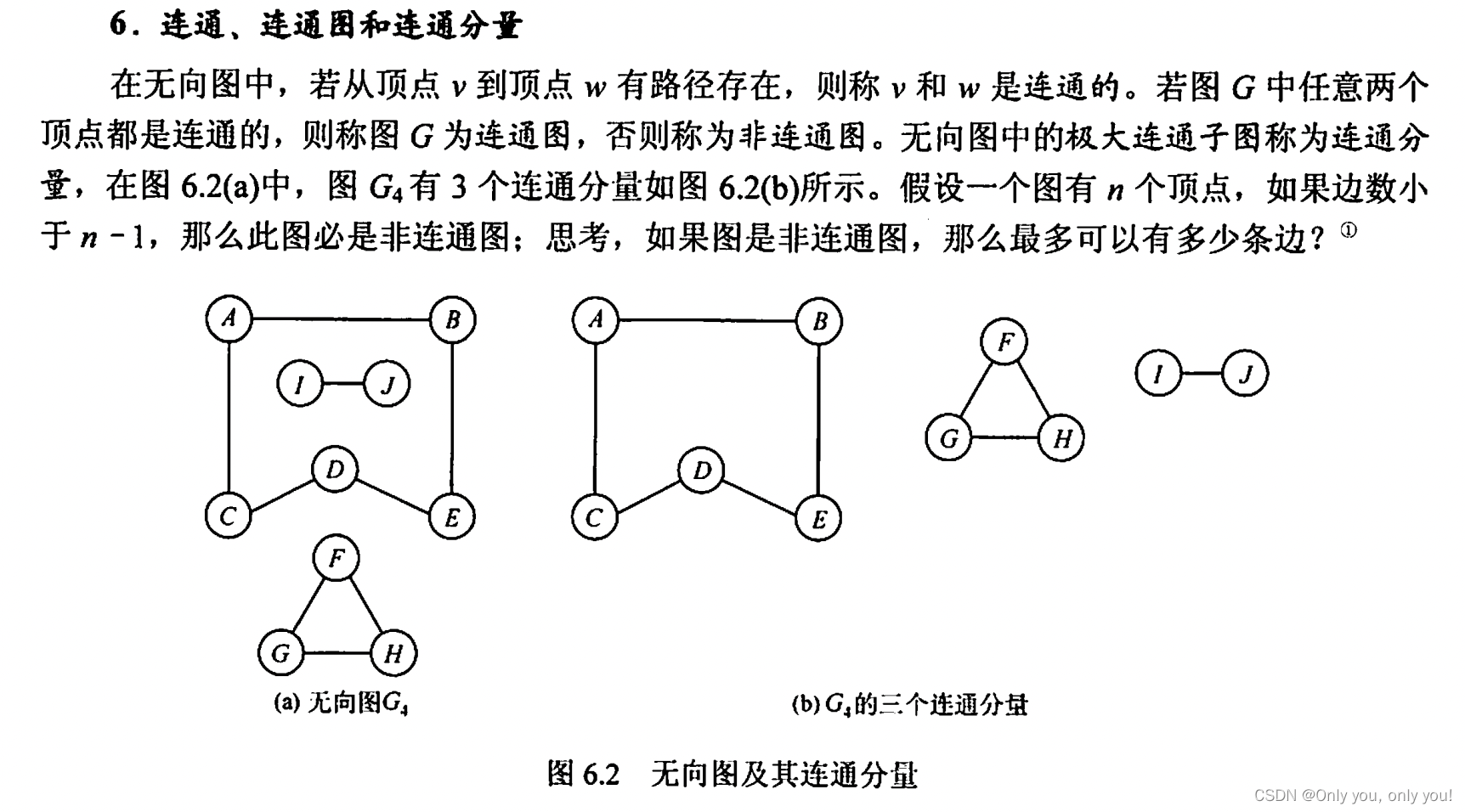
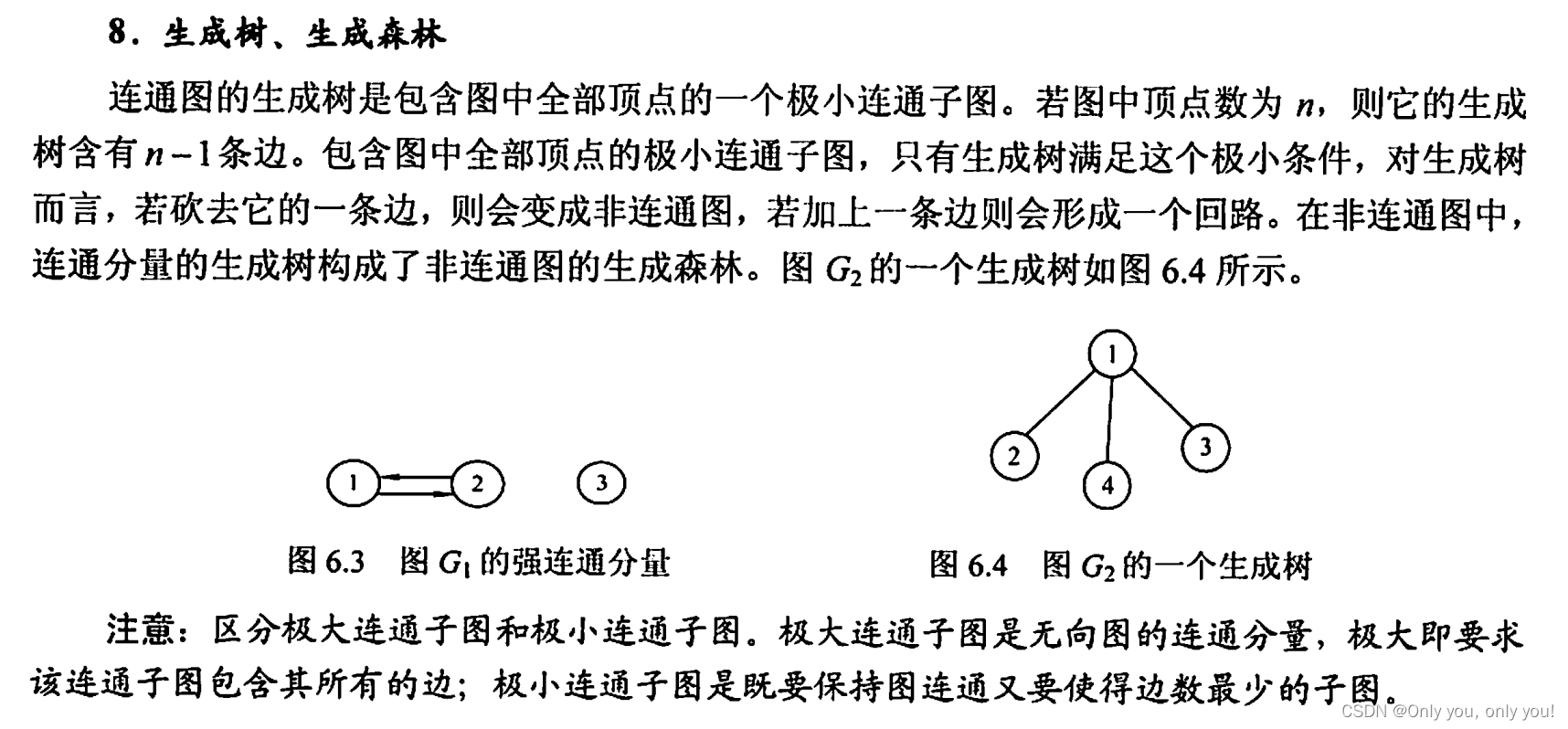
在这里插入图片描述

错题

在这里插入图片描述

图

图的基本概念

在这里插入图片描述

图的存储及基本操作

邻接矩阵
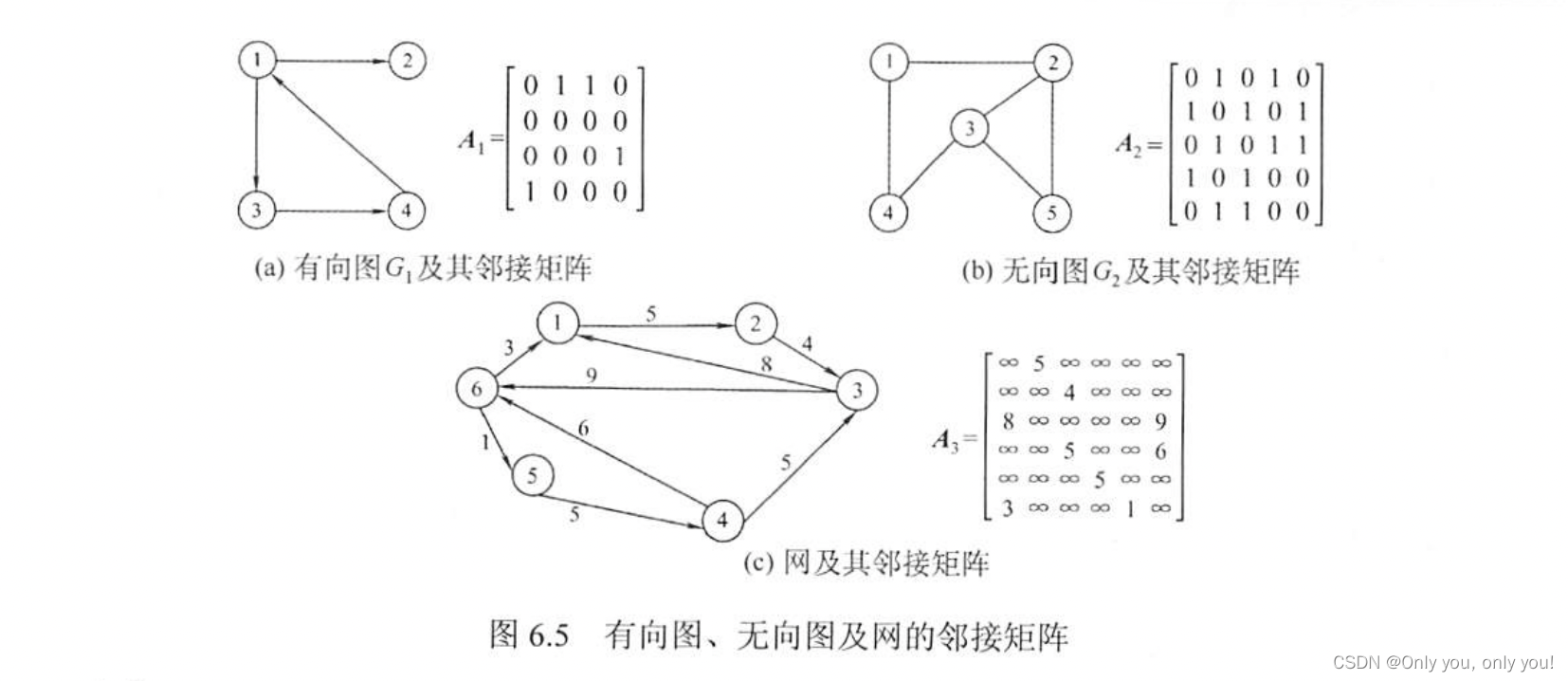
在这里插入图片描述

邻接表

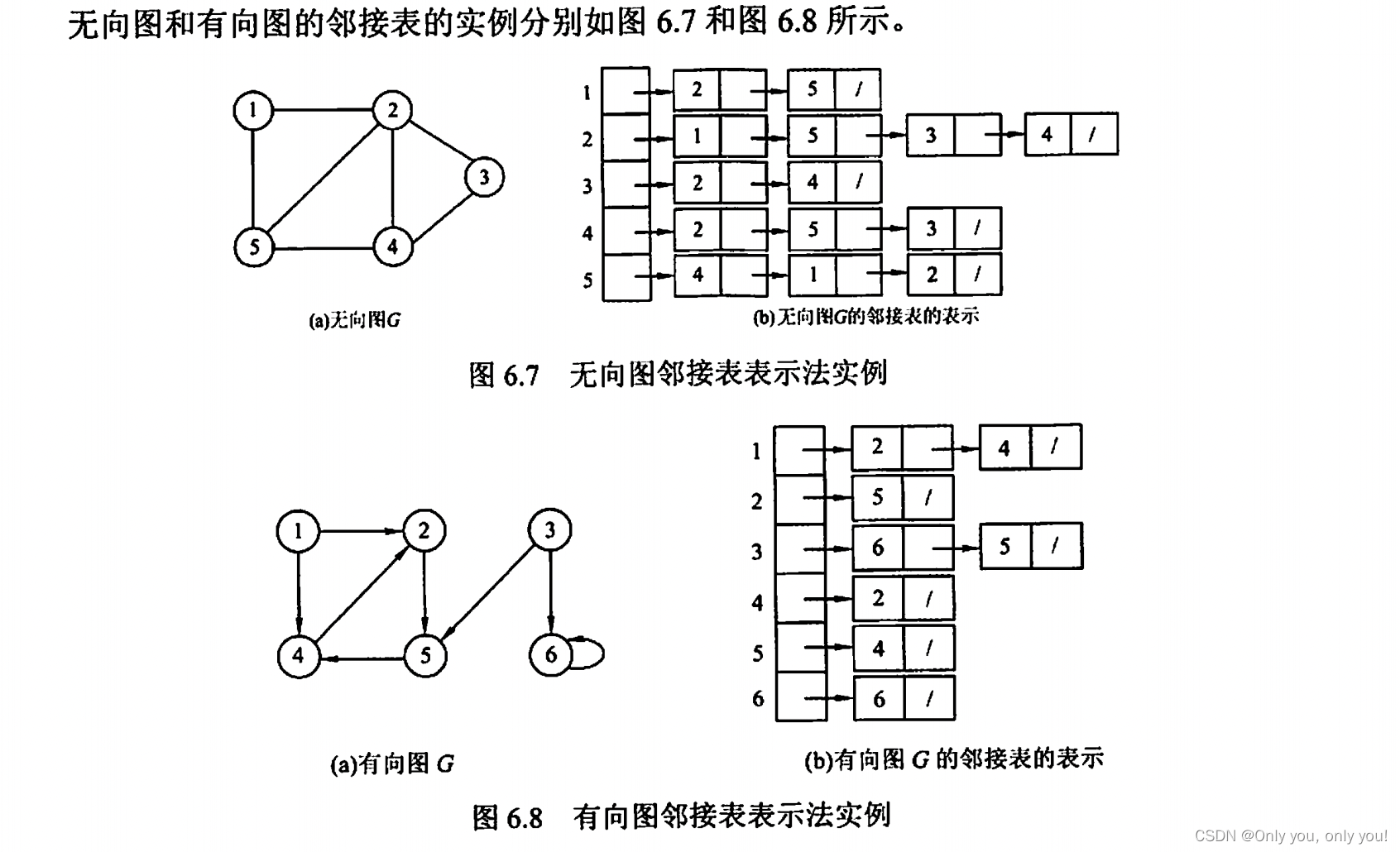
在这里插入图片描述

十字链表

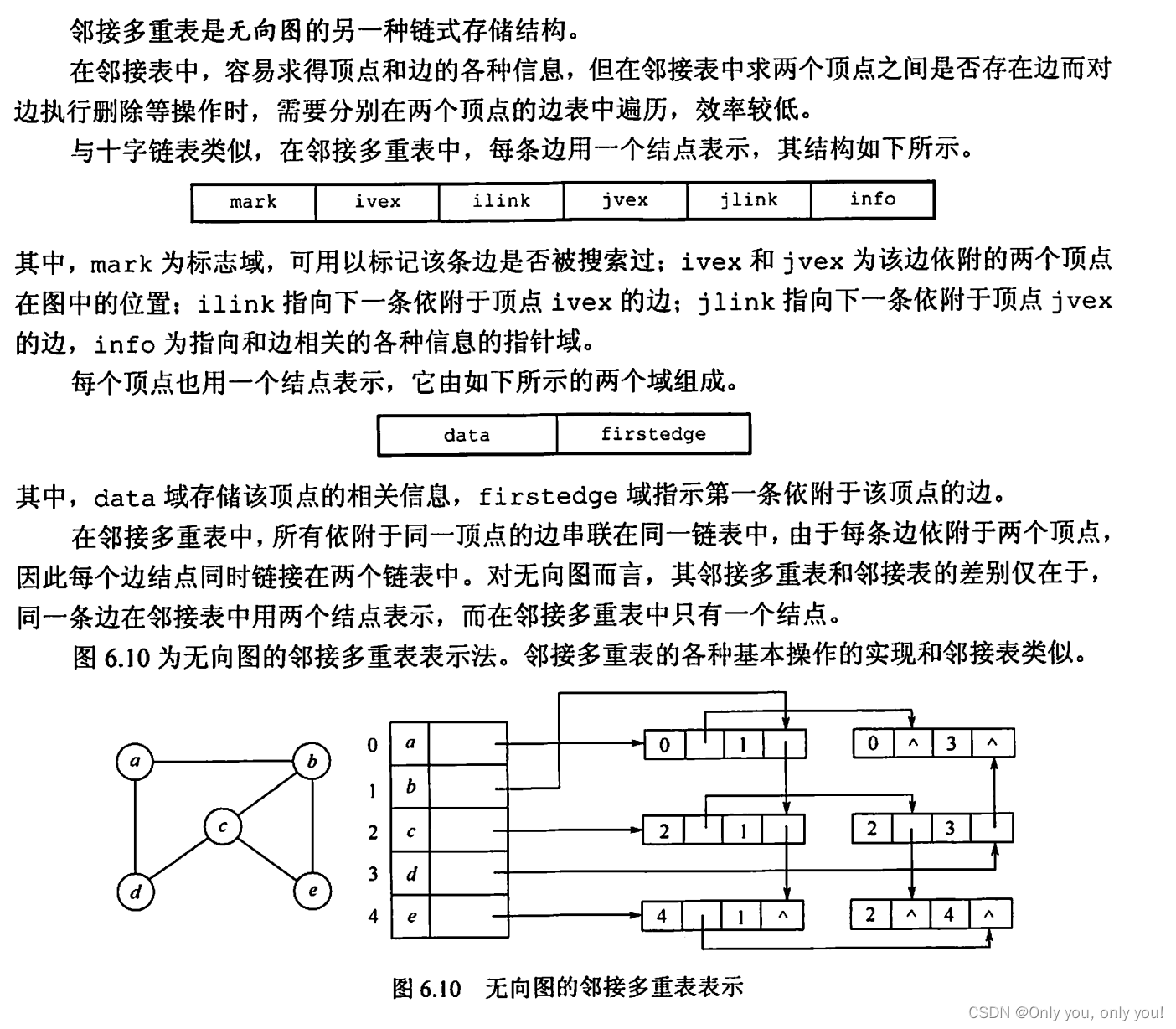
在这里插入图片描述

邻接多重表

在这里插入图片描述

图的遍历

#include<cstdlib>
#include<queue>

using namespace std;

#define MaxVertexNum 100

typedef char VertexType;
typedef int EdgeType;

typedef struct Graph {
    VertexType vertex[MaxVertexNum];
    EdgeType edge[MaxVertexNum][MaxVertexNum];
    int vertexNum, edgeNum;
} Graph;

void bfs(Graph G, int v, bool vis[]) {
    queue<int>que;
    vis[v] = true;
    que.push(v);
    while (!que.empty()) {
        int vertexIdx = que.front();
        // process code
        que.pop();
        for (int i = 0; i < G.vertexNum; i++) {
            if (!vis[i] && G.edge[vertexIdx][i] == 1) {
                    vis[i] = 1;
                    que.push(i);
            }
        }
    }
}
// 广度优先遍历。空间复杂度 O(|V|)；时间复杂度，邻接表方式是 O(|V| + |E|)，邻接矩阵方式是 O(|V|^2)
void bfs(Graph G) {
    bool *vis = (bool *)malloc(sizeof(int) * MaxVertexNum);
    for(int i = 0; i < MaxVertexNum; i++) {
        vis[i] = false;
    }
    for(int i = 0; i < G.vertexNum; i++) {
        if(!vis[i]) {
            bfs(G, i, vis);  // 每一个连通分量调用一次
        }
    }
}

void dfs(Graph G, int v, bool vis[]) {
    vis[v] = true;
    // process code
    for(int i = 0; i < G.vertexNum; i++) {
        if(!vis[i] && G.edge[v][i] == 1) {
            dfs(G, i, vis);
        }
    }
}
// 深度优先遍历。空间复杂度 O(|V|)；时间复杂度，邻接表方式是 O(|V| + |E|)，邻接矩阵方式是 O(|V|^2)
void dfs(Graph G) {
    bool *vis = (bool *)malloc(sizeof(int) * MaxVertexNum);
    for(int i = 0; i < MaxVertexNum; i++) {
        vis[i] = false;
    }
    for(int i = 0; i < G.vertexNum; i++) {
        if(!vis[i]) {
            dfs(G, i, vis);  // 每一个连通分量调用一次
        }
    }
}

图的应用

最小生成树

参考文章

所谓最小生成树，就是在一个具有N个顶点的带权连通图G中，如果存在某个子图G’，其包含了图G中的所有顶点和一部分边，且不形成回路，并且子图G’的各边权值之和最小，则称G’为图G的最小生成树。
由定义我们可得知最小生成树的三个性质：
•最小生成树不能有回路
•最小生成树可能是一个，也可能是多个（权值相同的边）
•最小生成树边的个数等于顶点的个数减一

Prim 算法，从任一结点出发，每次找到当前已选结点们最近那个结点，加入到已选结点中，直到全部结点都已选出。
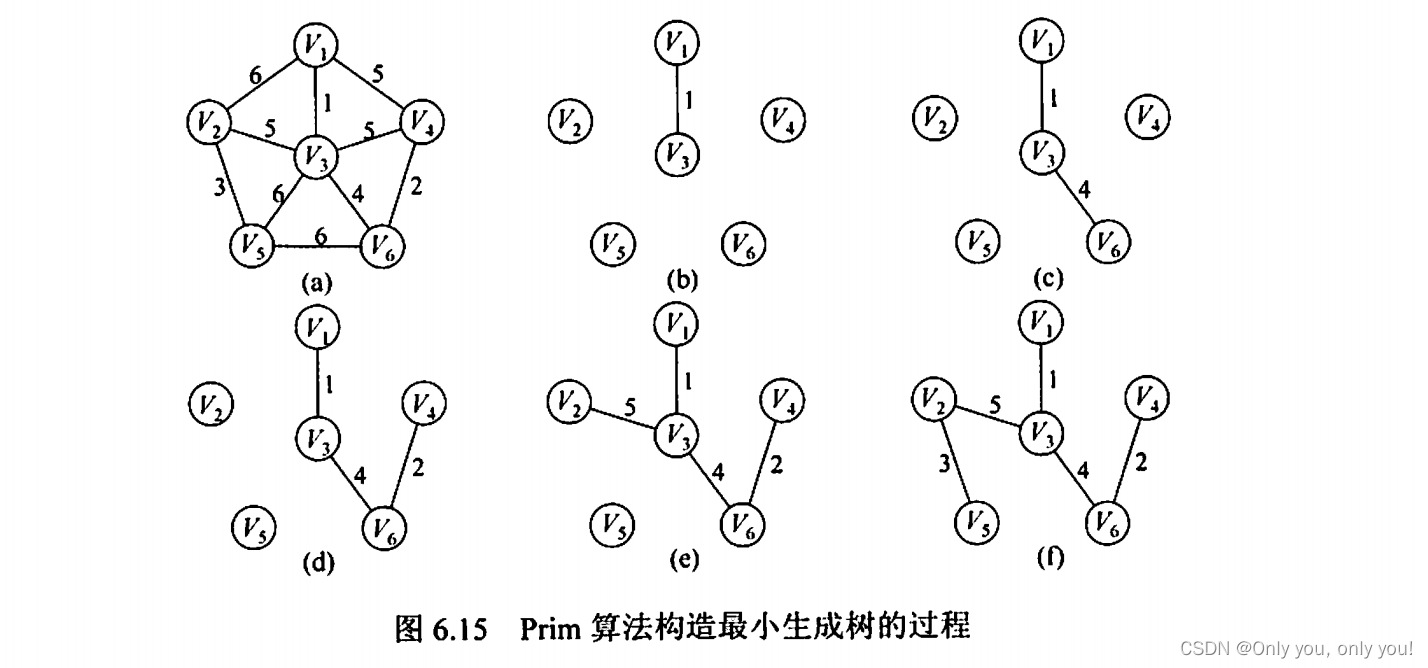
在这里插入图片描述

Kruscal 算法，每次选最小权的边及其结点（该边的两个结点不能都已选中），直到选出所有结点。
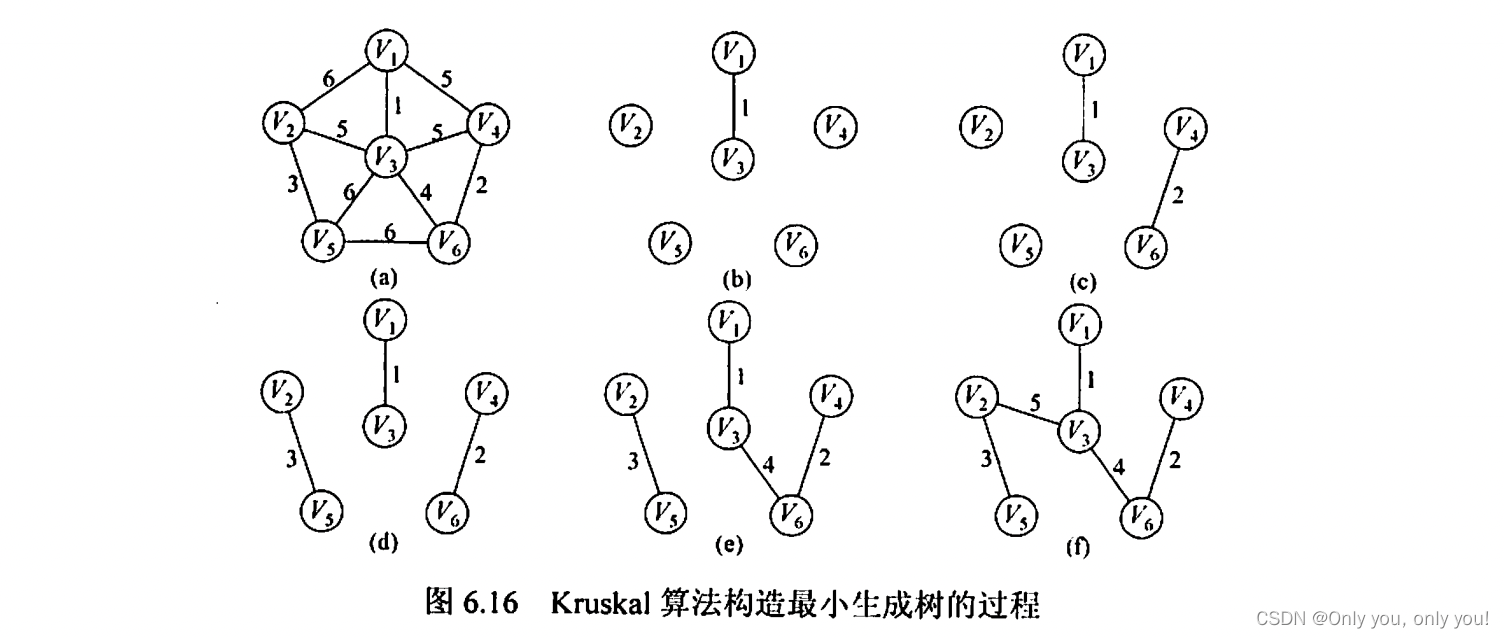
在这里插入图片描述

最短路径

参考文章

Dijkstra 算法，带权有向图单源最短路径，时间复杂度 O(|V|^2)
每轮选最小距离的结点继续扩展。
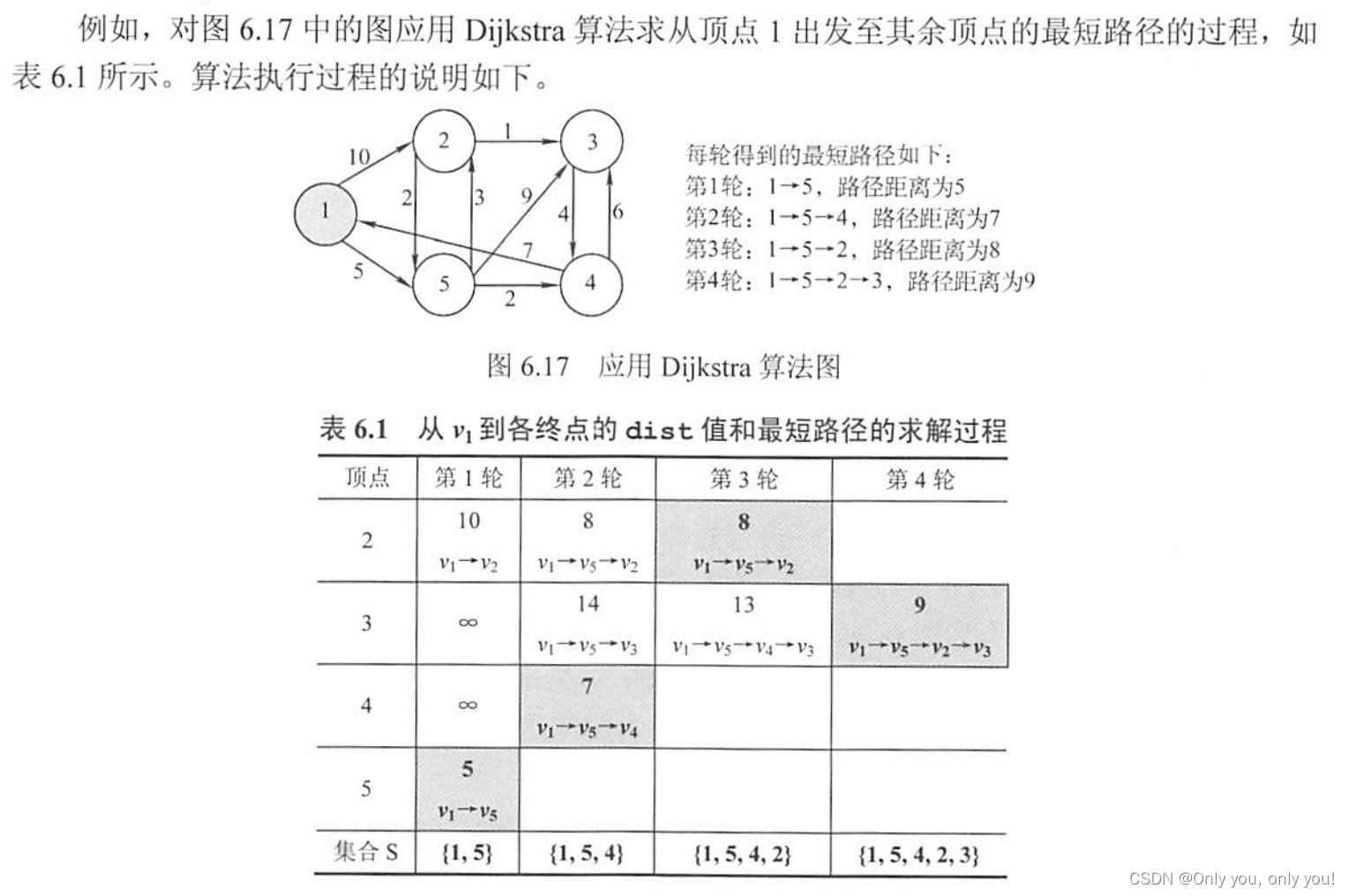
Floyd 算法，带权有向图任意一对结点最短路径，时间复杂度 O(|V|^3)

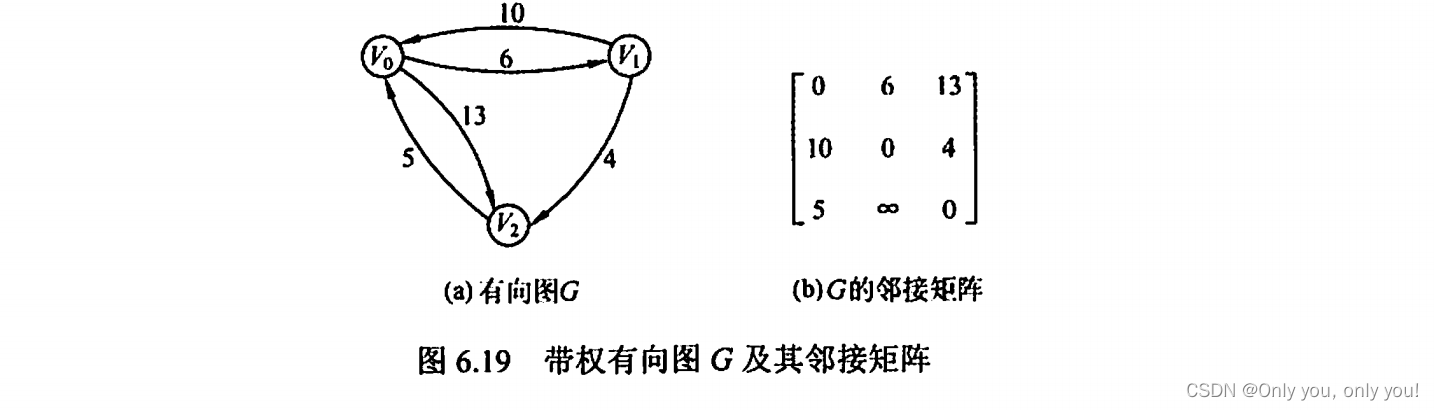
每轮分别把 V0、V1 和 V2 作为中间结点，更新所有对结点之间的最小路径值！

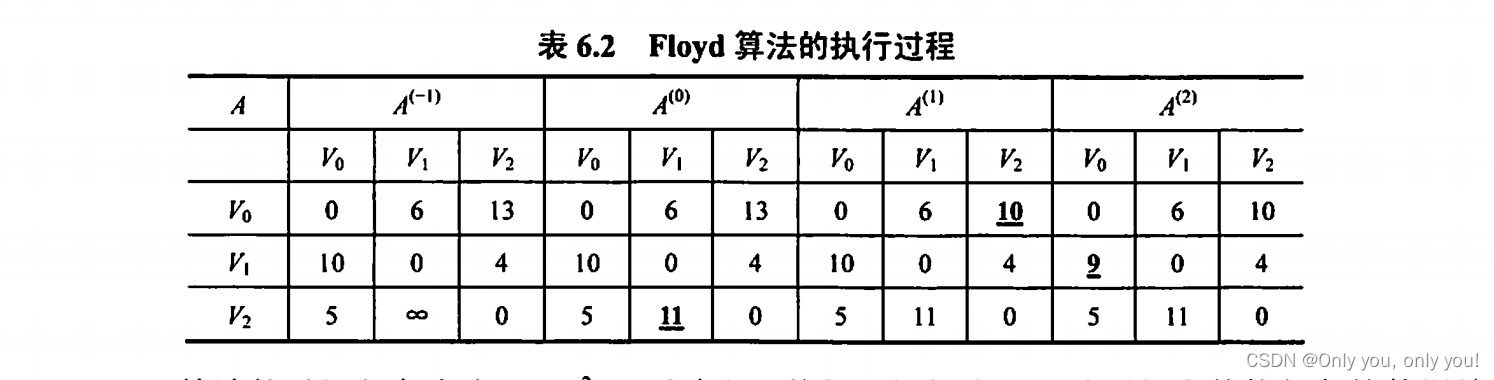
有向无环图描述表达式

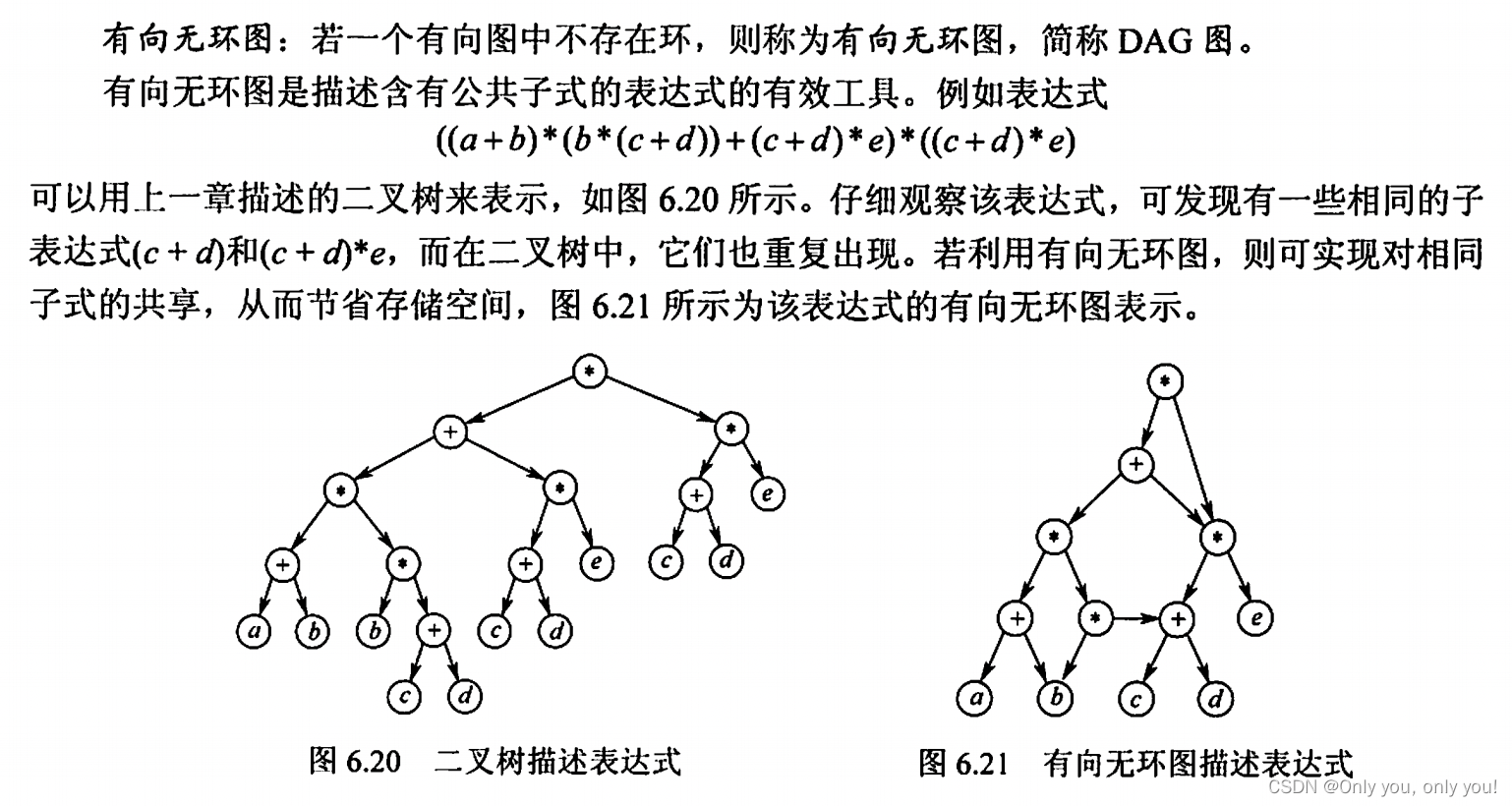
在这里插入图片描述

拓扑排序

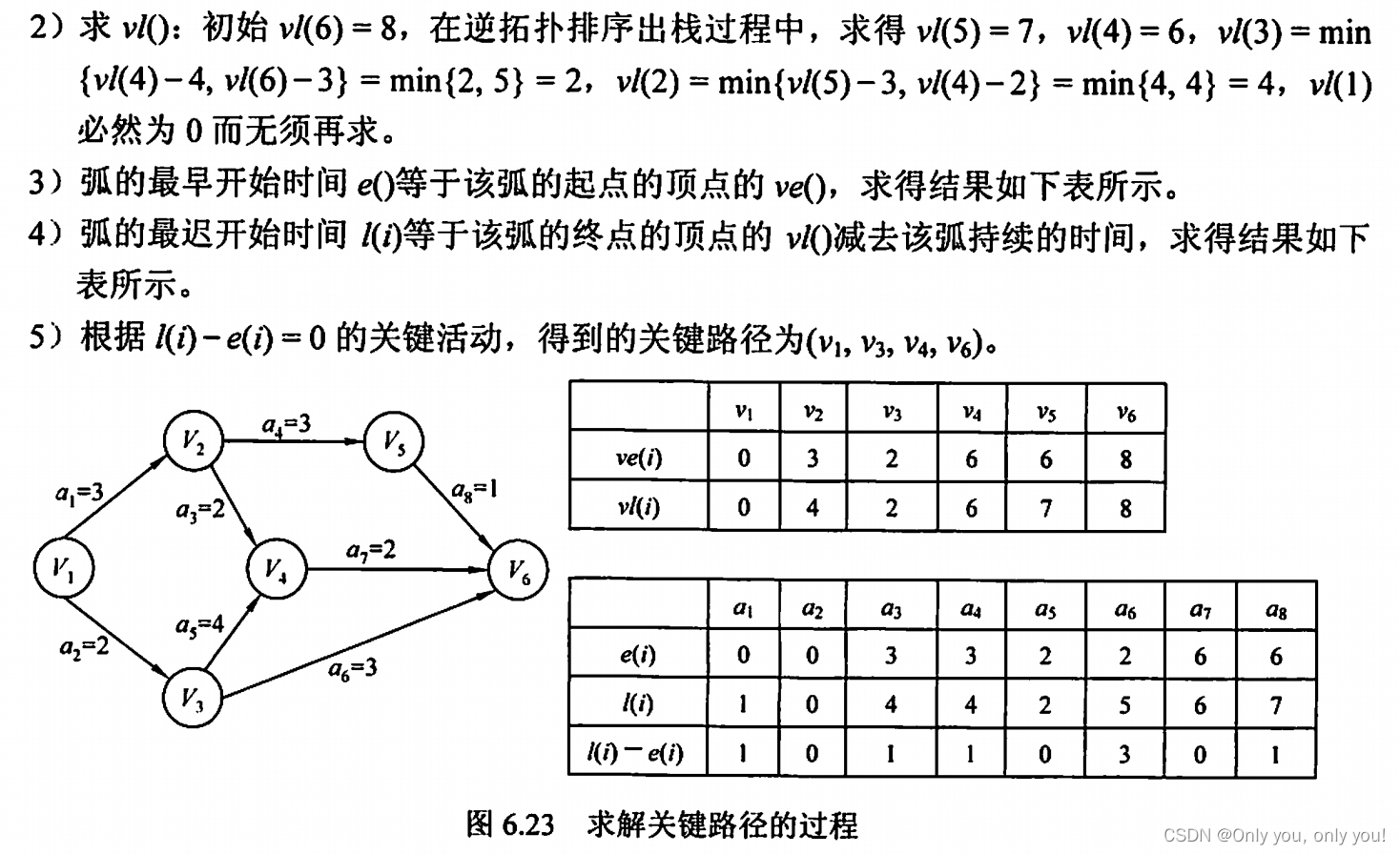
在这里插入图片描述

关键路径
在这里插入图片描述

在这里插入图片描述

错题

在这里插入图片描述
解答：先用 6 个顶点做一个完全图，需要 6 * (6 - 1) / 2 = 15 条边，再用 1 条边把第 7 个顶点连上，至少需要 16 条边，保证任何情况下 G 是连通的。

在这里插入图片描述
解答：画图，要遍历完所有结点（所有连通分量），共 5 种可能情况。

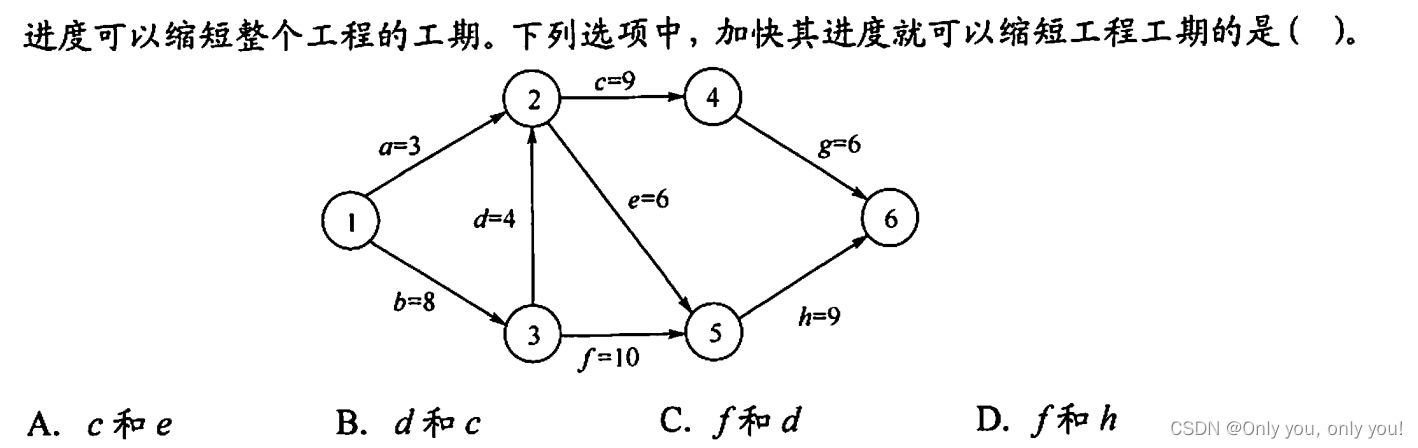
在这里插入图片描述

解答：计算 ve 的过程其实就能得到关键活动了，关键路径是 bdcg、bdeh 和 bfh，要想缩短工期，答案选项中得覆盖到所有关键路径，选 C。

在这里插入图片描述
解答：特殊例子，二叉树后序遍历，就是执行输出语句后立刻退出递归的，正好就是逆拓扑排序。

查找

顺序查找

二分查找

分块查找

在这里插入图片描述

树型查找

二叉排序树

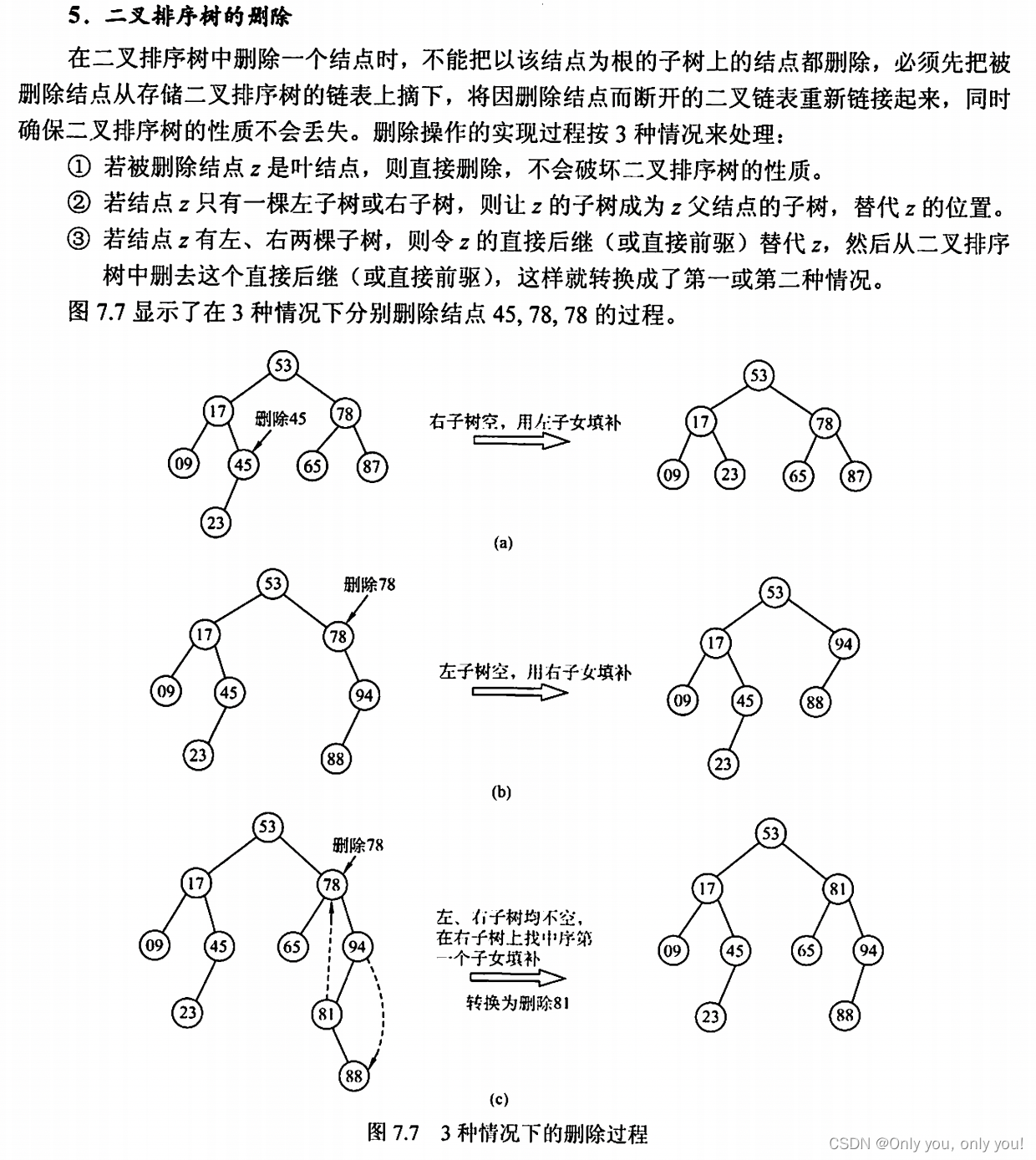
在这里插入图片描述

平衡二叉树（AVL）

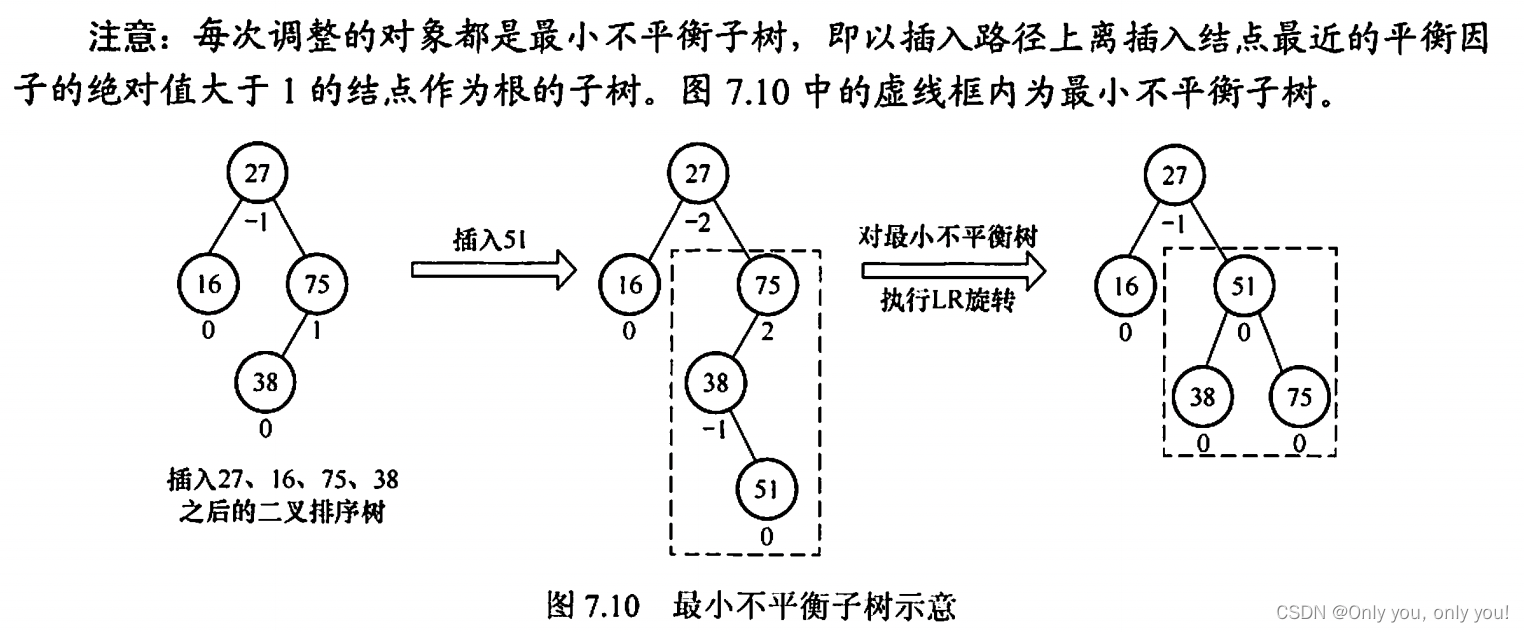
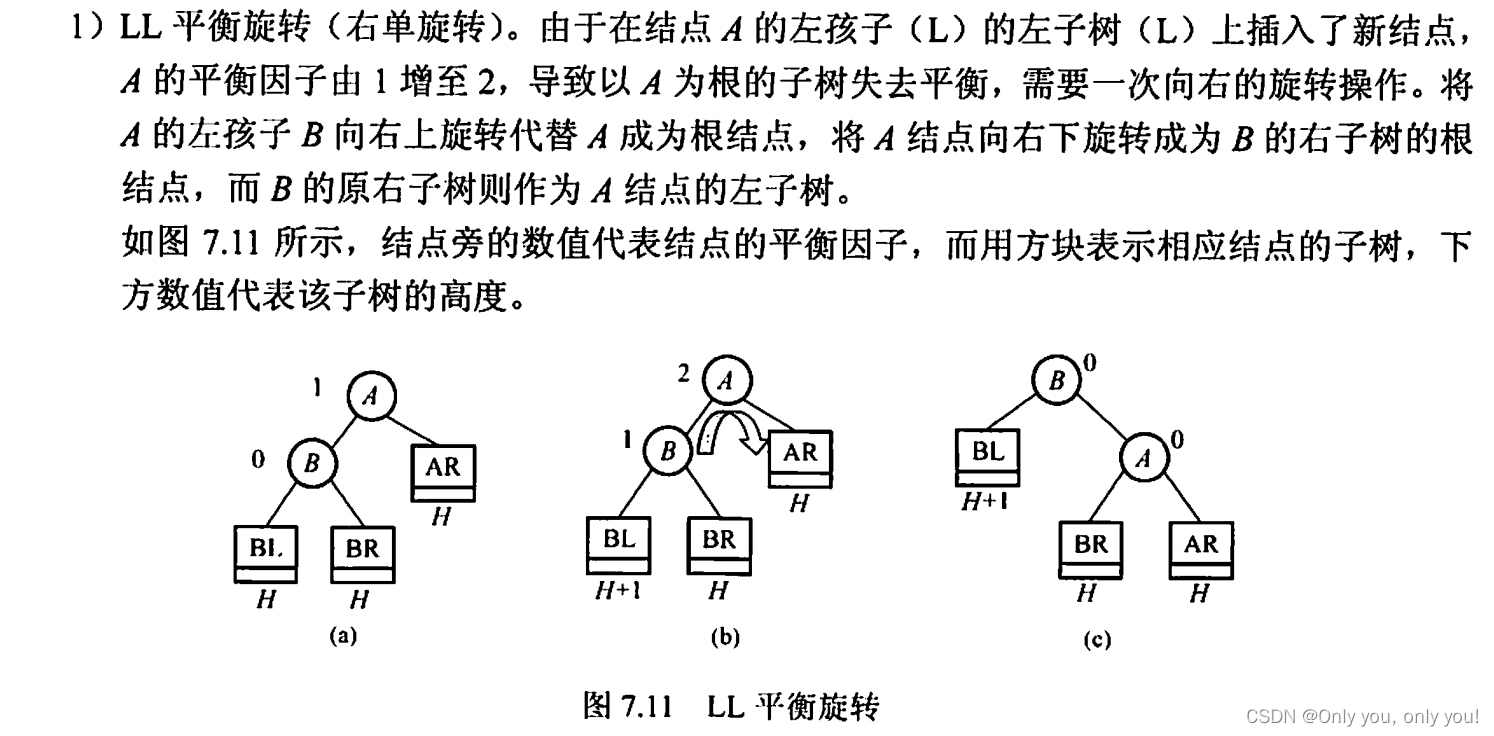
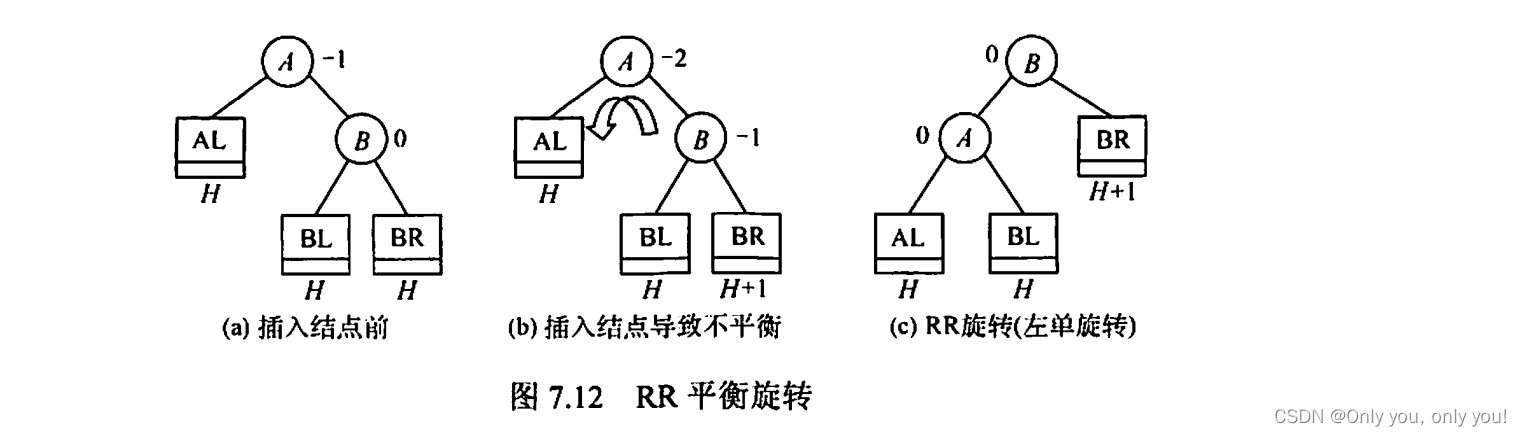
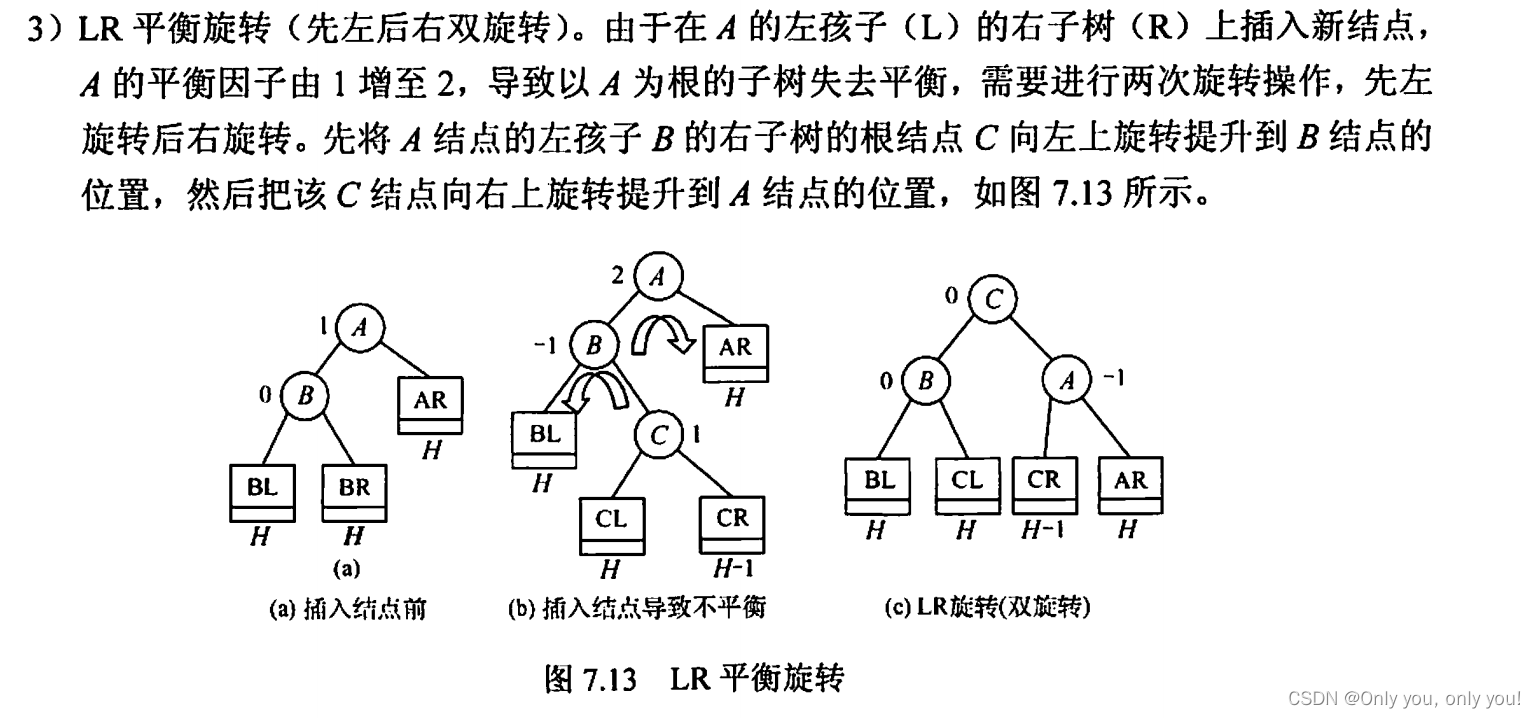
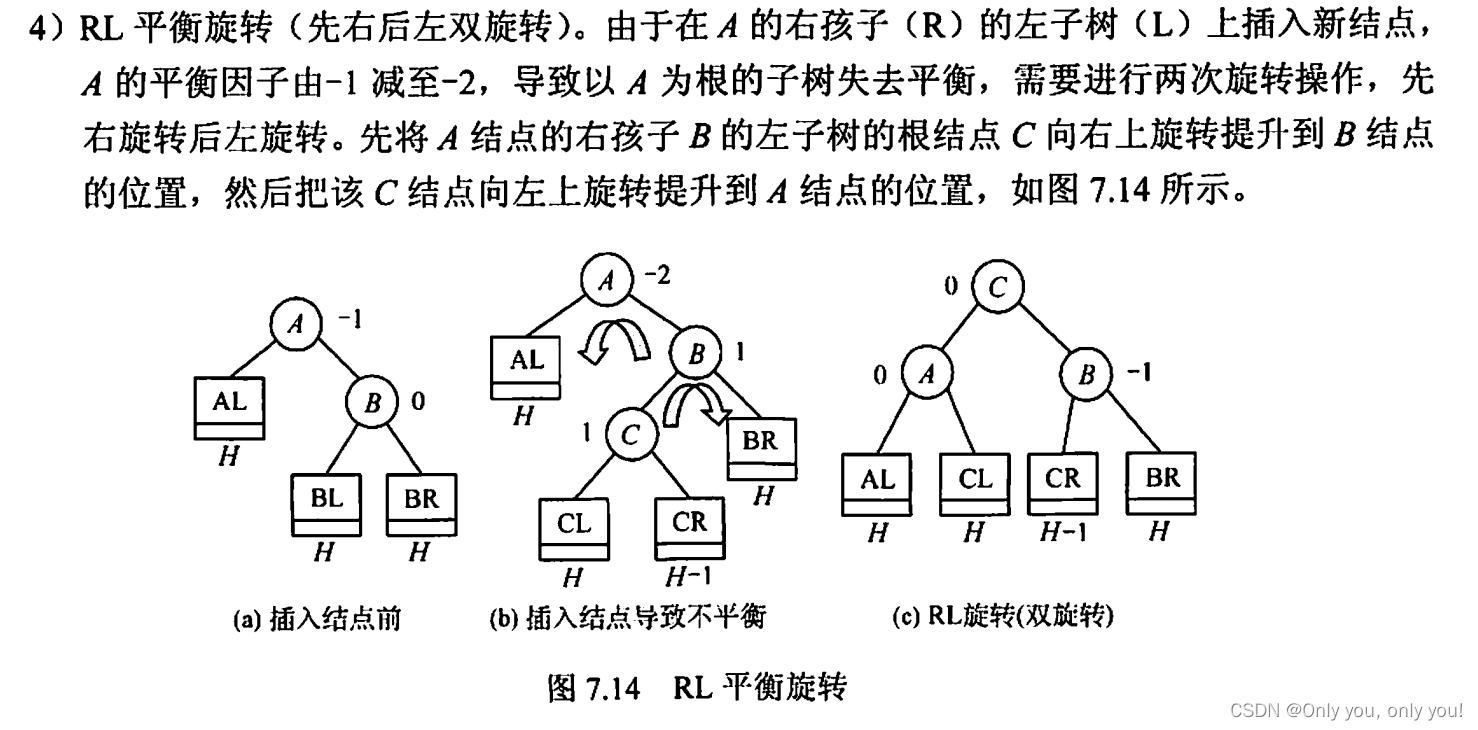
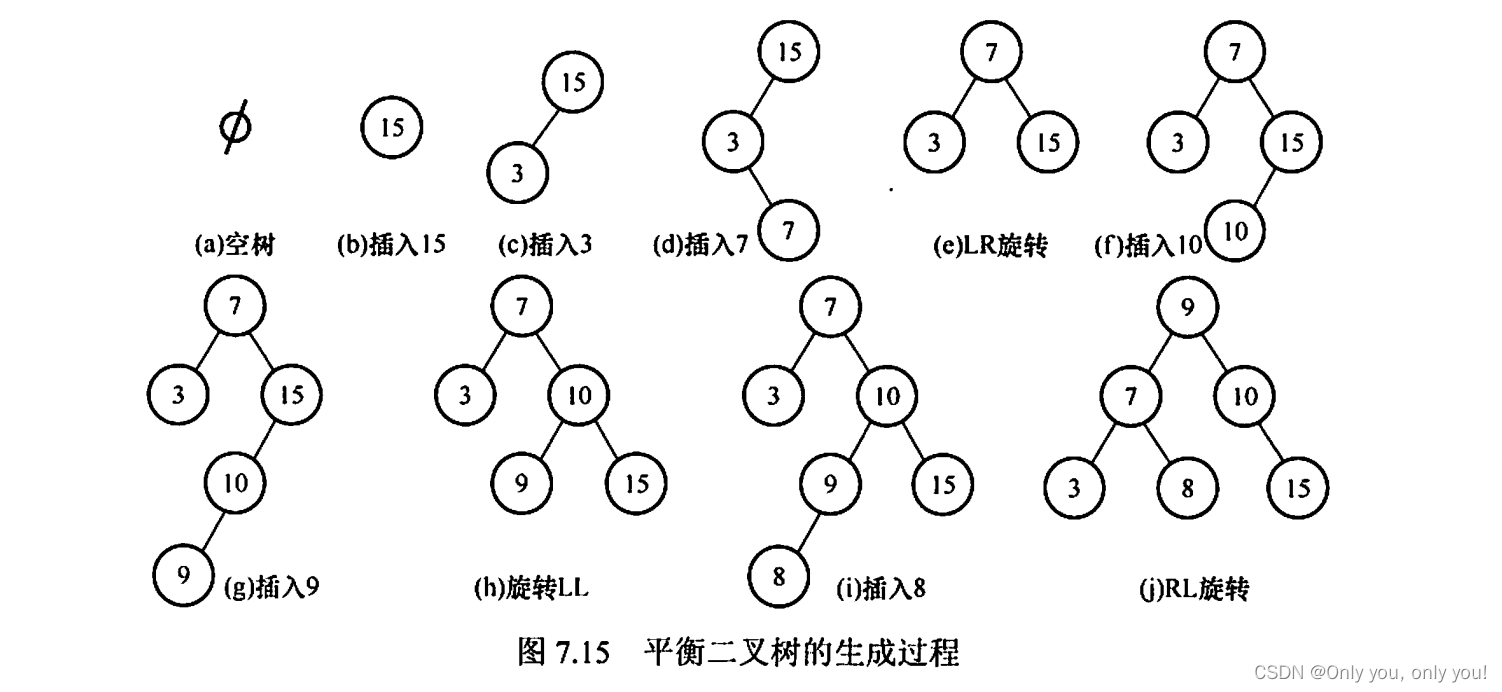
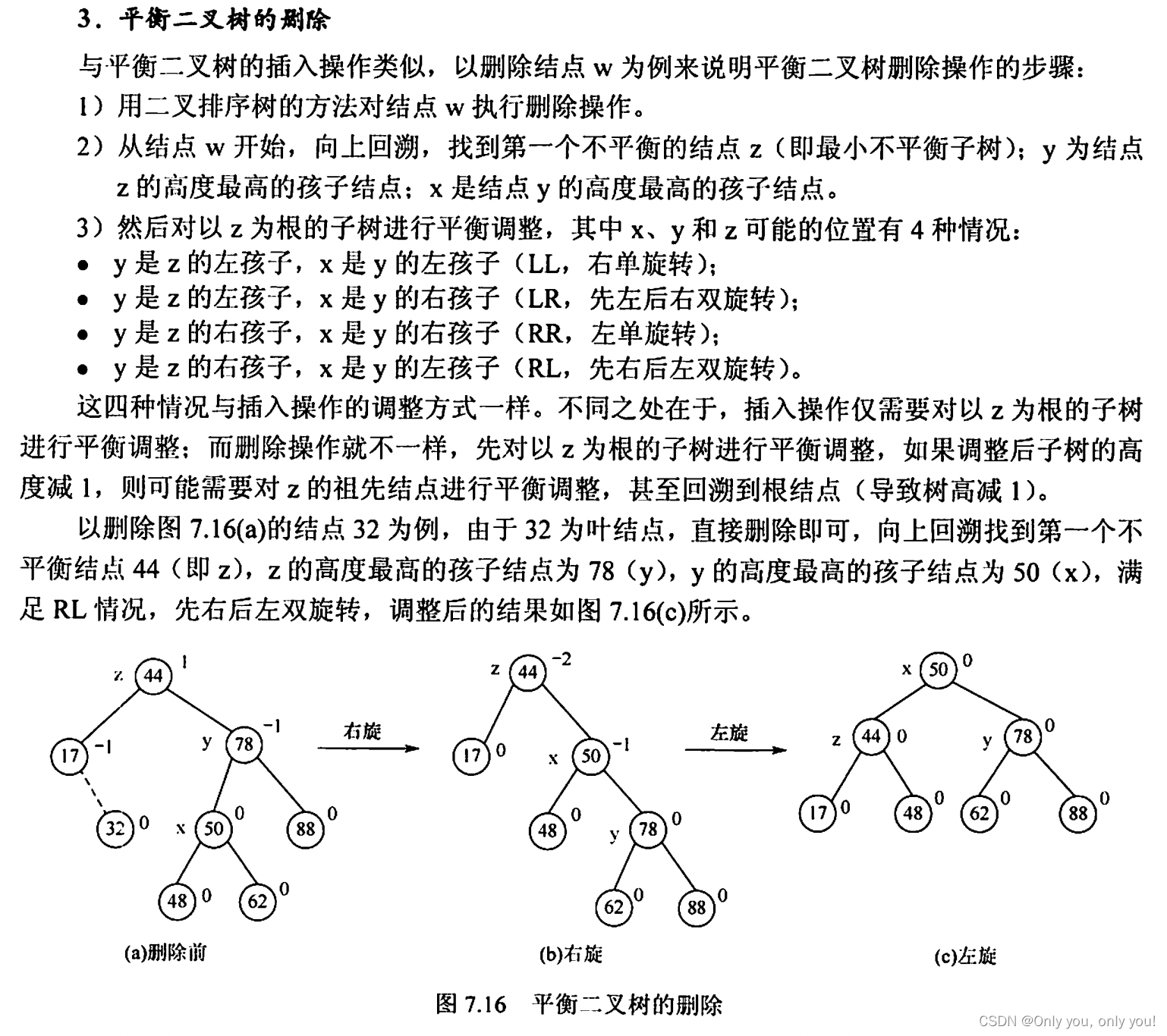
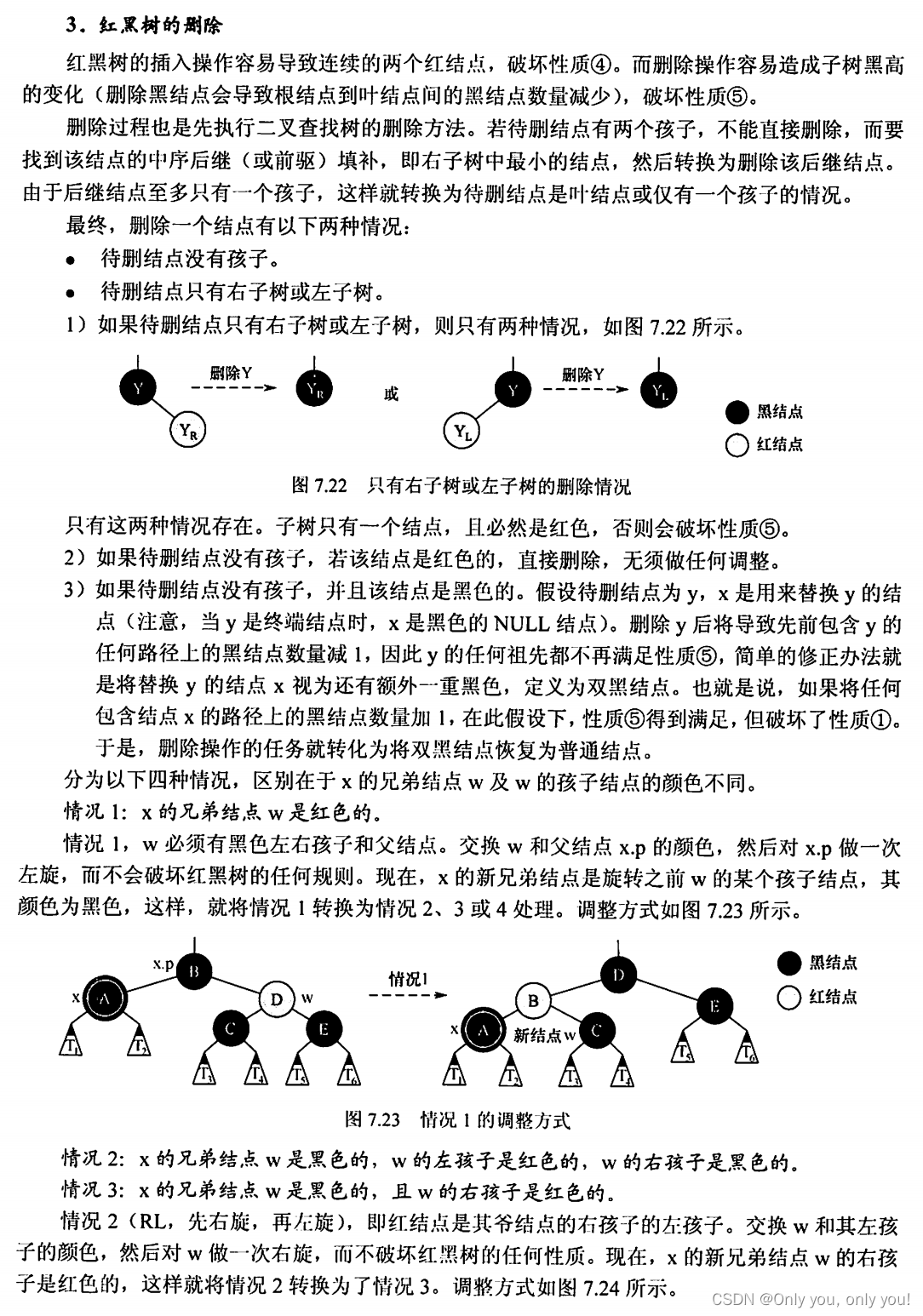
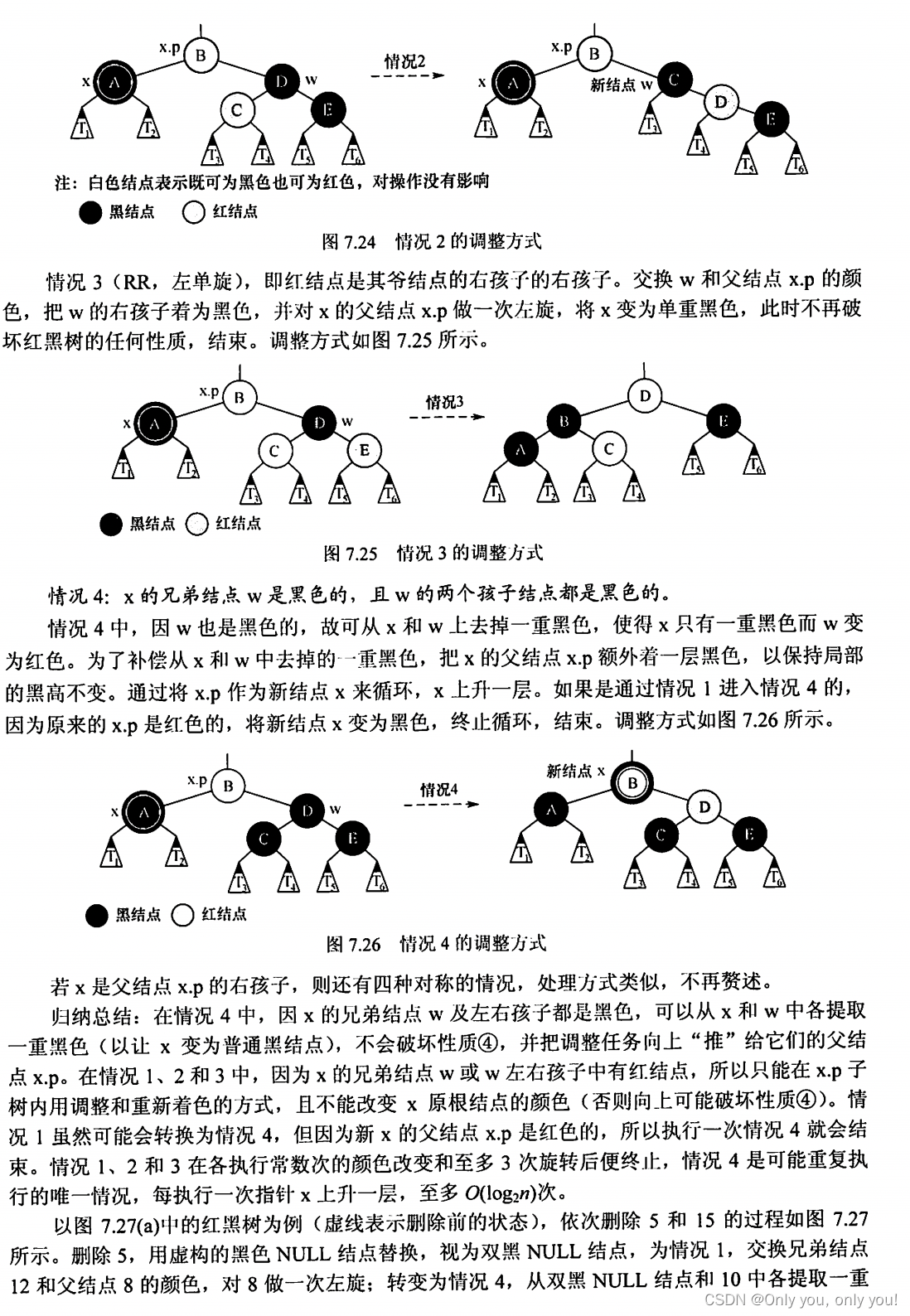
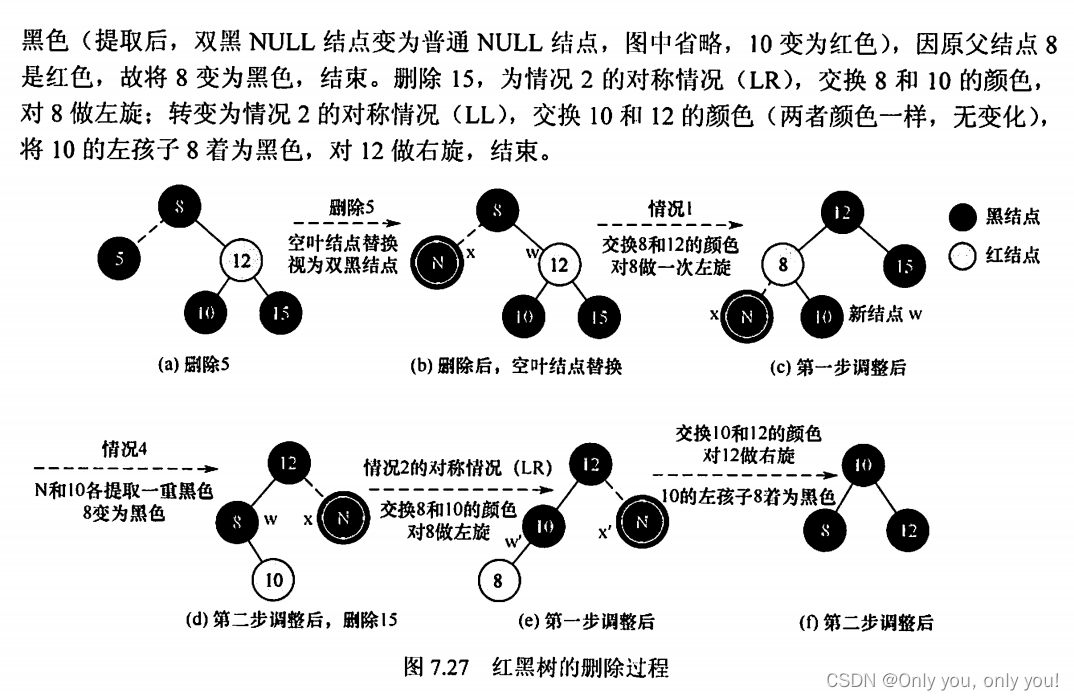
在这里插入图片描述

红黑树

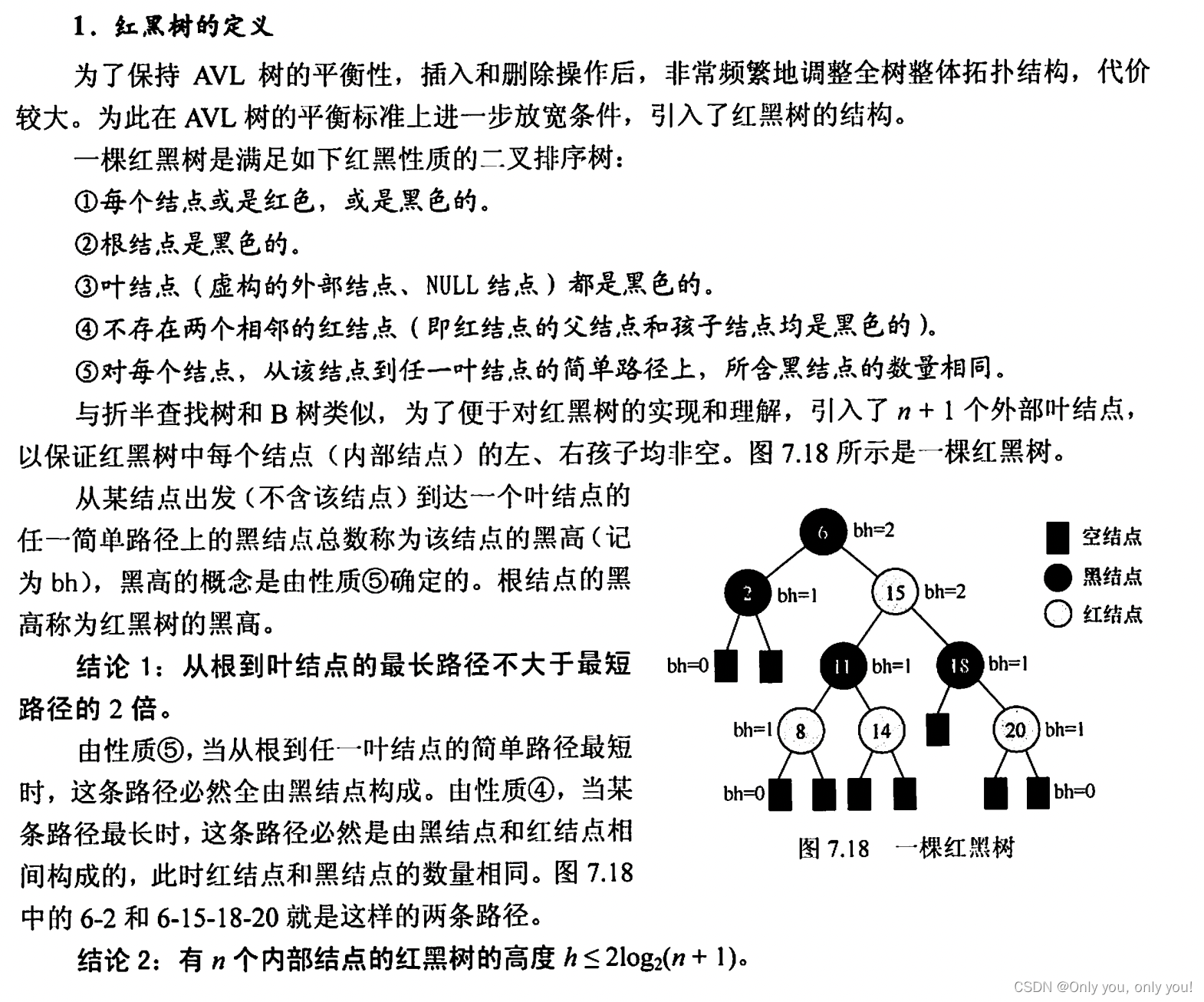
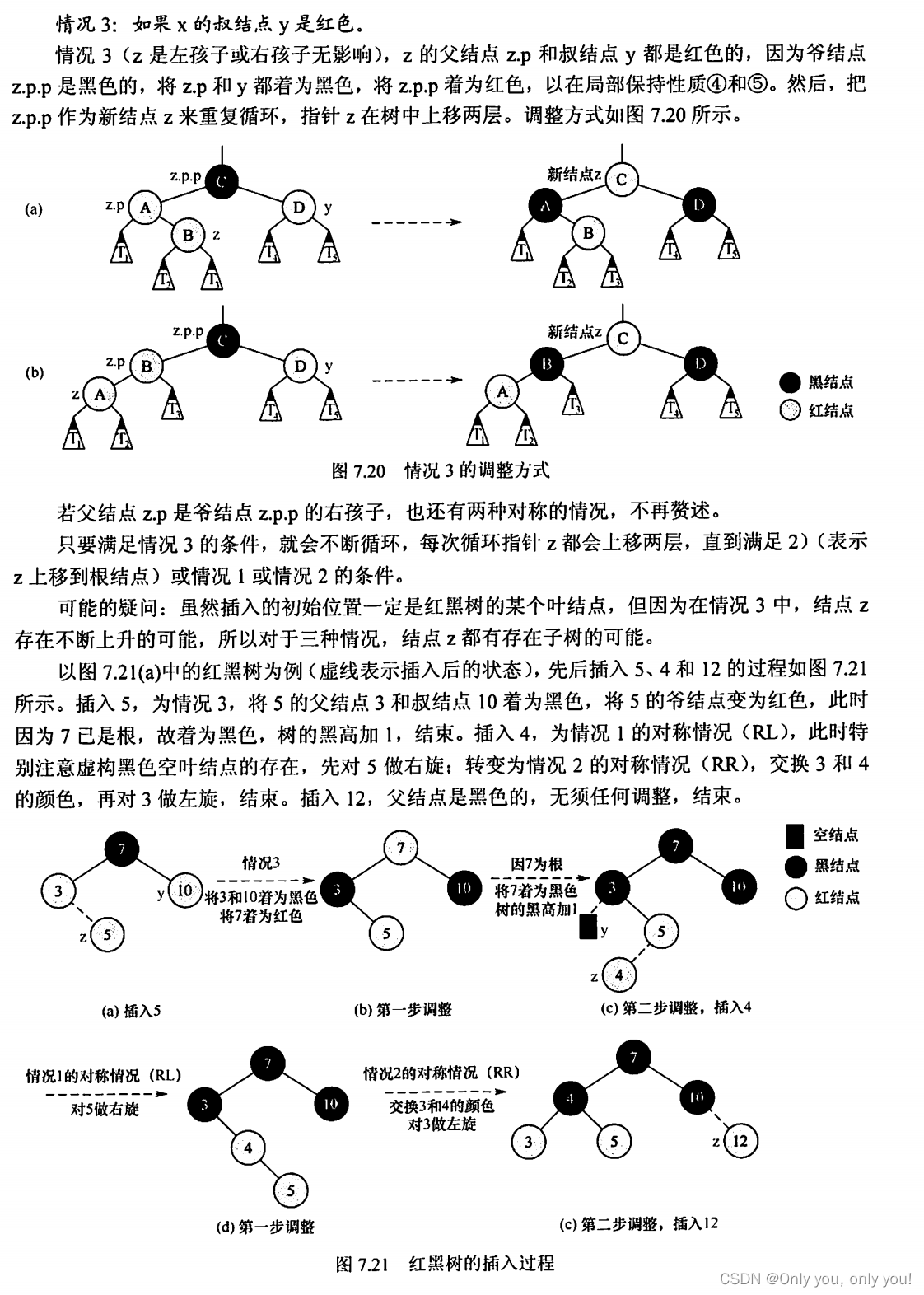
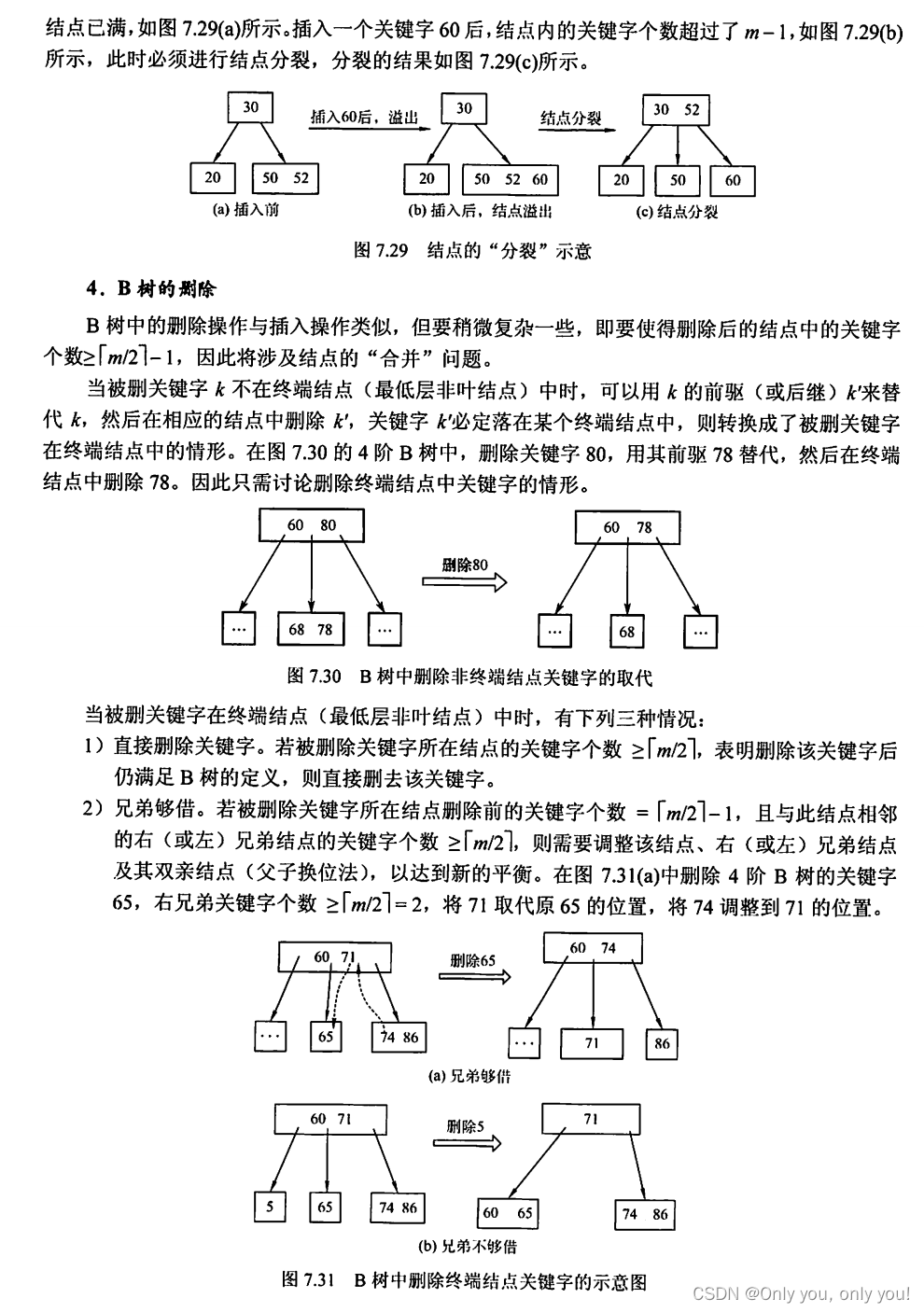
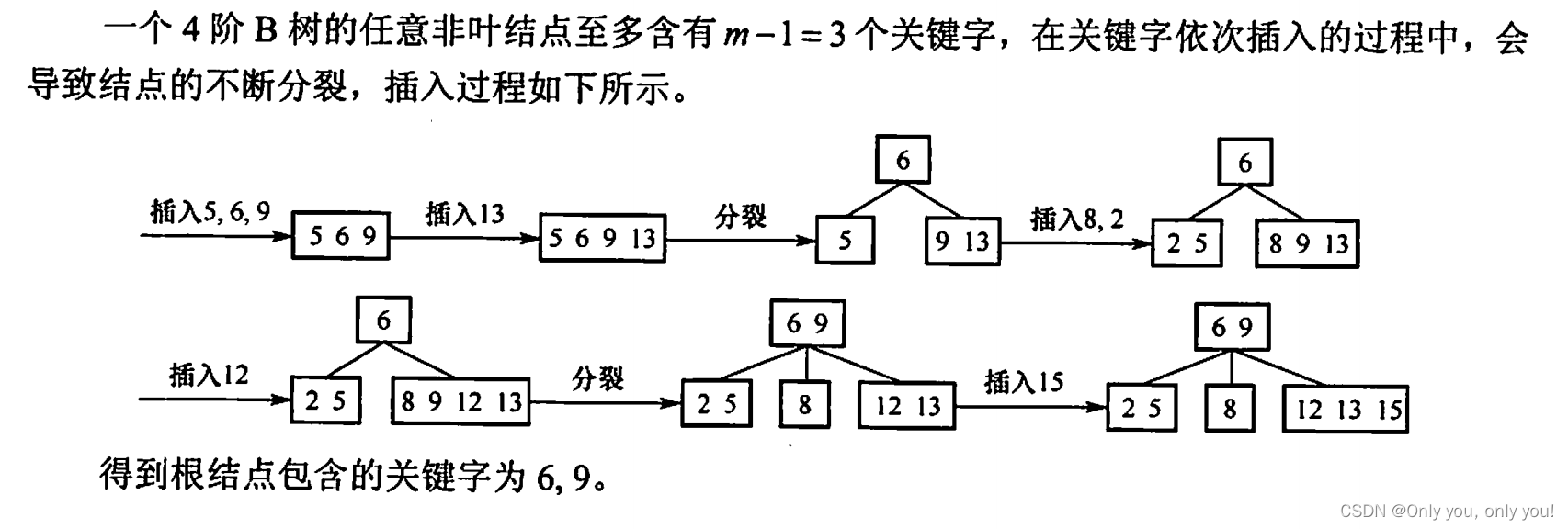
在这里插入图片描述

B树和B+树

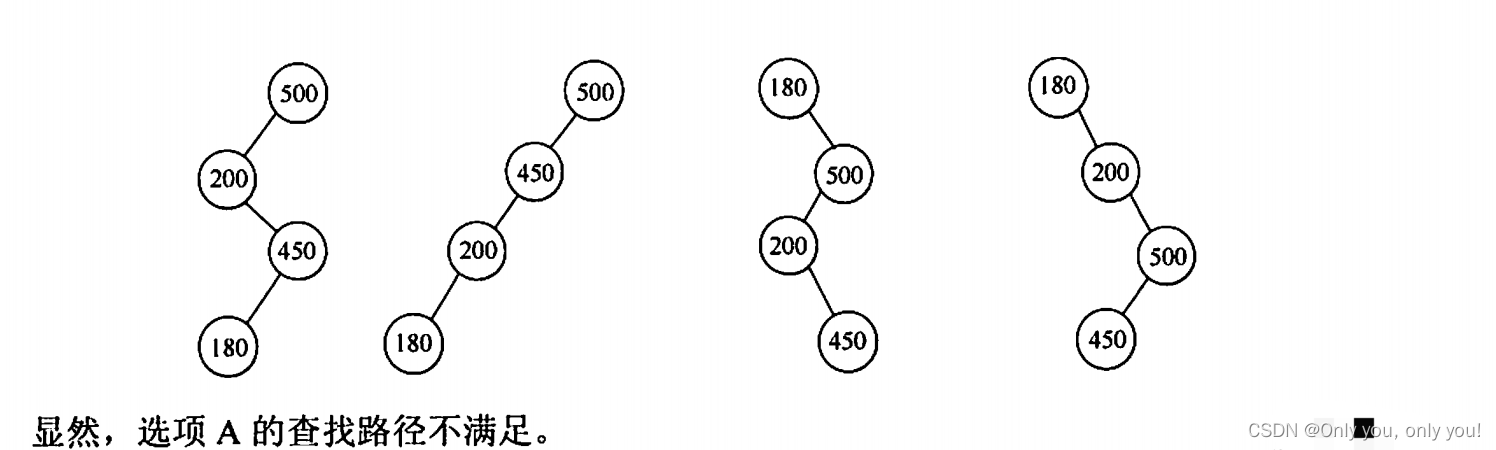
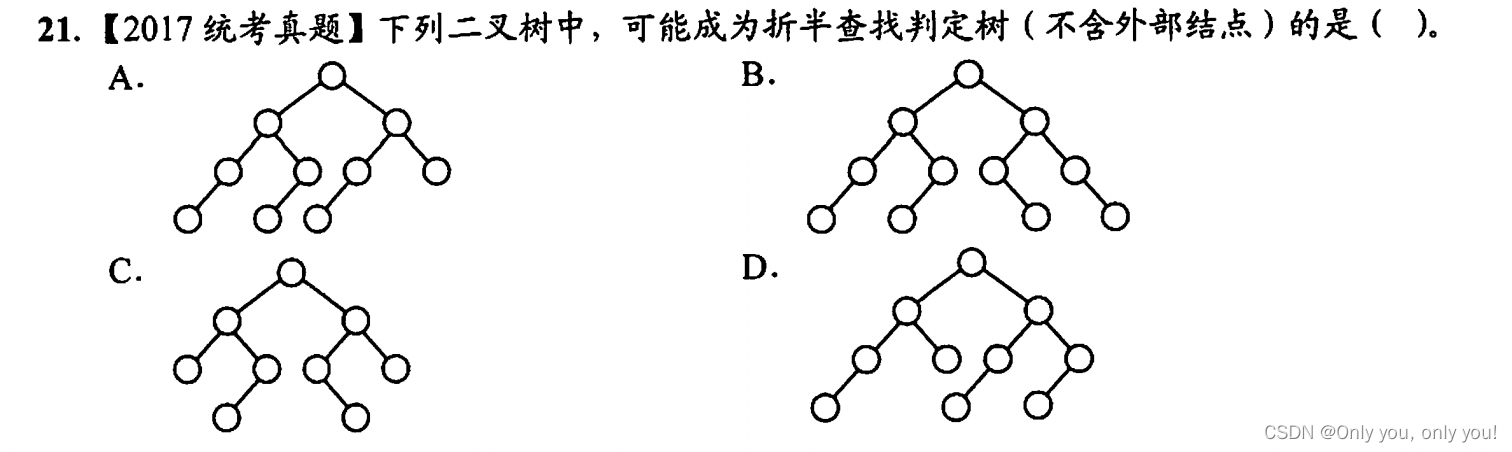
在这里插入图片描述

散列表

在这里插入图片描述

错题

在这里插入图片描述

在这里插入图片描述

解答：折半查找判定树是搜索二叉树，不妨先把各结点填上值，再判断计算 mid 时是否都统一向上取整或向下取整了，如果不统一就不对！以选项 C 为例，4 号结点是小于 5 大于 2 的情况下算出来的，即 (2 + 5) / 2 = 4，向上取整，而 6 号结点是大于 5 小于 8 的情况下算出来的，即 (5 + 8) / 2= 6，向下取整，这说明 mid 计算取整方向没有统一，错误。同样可以验证得到 B 选项和 D 选项都是错误的。
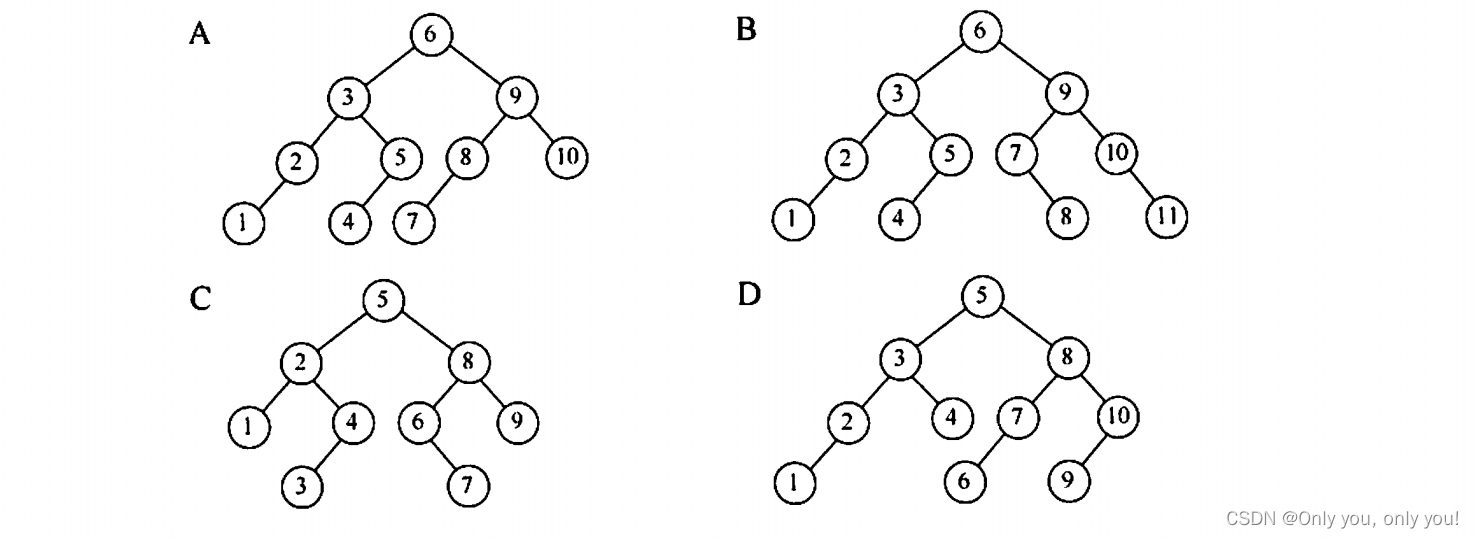
在这里插入图片描述

在这里插入图片描述
答案：A

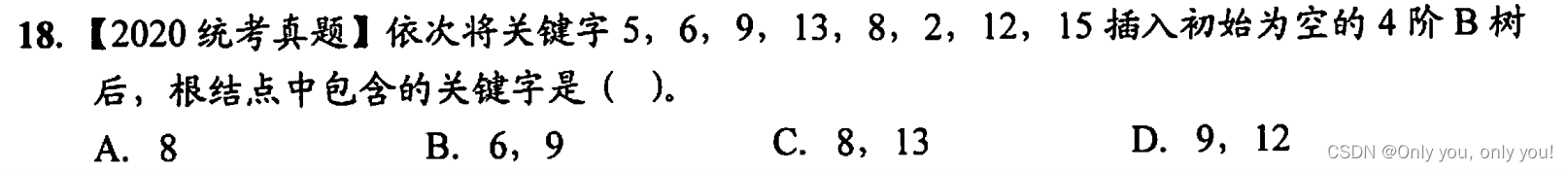
在这里插入图片描述

排序

在这里插入图片描述

#include<cmath>

// 为方便写代码，不爆红，不妨如此定义一下
typedef int ElementType;

// ----- 8.2.1 直接插入排序 -----

void swap(ElementType a[], int x, int y) {
    int t = a[x];
    a[x] = a[y];
    a[y] = t;
}
// 稳定，适用顺序表和链表
void insertSort(ElementType a[], int n) {
    if(n < 2) {
        return;
    }
    for(int i = 1; i < n; i++) {
        for(int j = i - 1; j >= 0 && a[j + 1] < a[j]; j--) {
            swap(a, j, j + 1);
        }
    }
}


// ----- 8.2.2 折半插入排序 -----

// 寻找小于等于 v 的最右元素的索引，若无，返回 -1
int binarySearch(ElementType a[], ElementType v, int st, int en) {
    int l = st, r = en;
    int idx = -1;
    while(l <= r) {
        int mid = l + (r - l) / 2;
        if(a[mid] <= v) {
            idx = mid;
            l = mid + 1;
        } else {
            r = mid - 1;
        }
    }
    return idx;
}
// 折半插入排序，待插入位置通过二分查找得到，再插入。稳定，适用顺序表
void insertSortBinary(ElementType a[], int n) {
    if(n < 2) {
        return;
    }
    for(int i = 1; i < n; i++) {
        int idx = binarySearch(a, a[i], 0, i - 1); // 待插入位置是 idx + 1
        ElementType data = a[i];
        for(int j = i - 1; j > idx; j--) {
            swap(a, j + 1, j);
        }
        a[idx + 1] = data;
    }
}


// ----- 8.2.3 希尔排序 -----

// 外层有个步长遍历，内层是直接插入排序。不稳定，适用顺序表。
void shellSortBinary(ElementType a[], int n) {
    if(n < 2) {
        return;
    }
    for(int step = n / 2; step >= 1; step /= 2) {
        for(int i = step; i < n; i += step) {
            for(int j = i - step; j >= 0 && a[j + step] < a[j]; j -= step) {
                swap(a, j, j + step);
            }
        }
    }
}


// ----- 8.3.1 冒泡排序 -----

void bubbleSort(ElementType a[], int n) {
    if(n < 2) {
        return;
    }
    bool flag = false;
    for(int i = n - 1; i > 0; i--) {
        flag = false;
        for(int j = 0; j < i; j++) {
            if(a[j] < a[j + 1]) {
                swap(a, j, j + 1);
                flag = true;
            }
        }
        if(!flag) {
            break;
        }
    }
}


// ----- 8.3.2 快速排序 -----

void quickSort(ElementType a[], int n) {
    if(n < 2) {
        return;
    }
    quickSort(a, 0, n - 1);
}
void quickSort(ElementType a[], int l, int r) {
    if(l < r) {
        int *pos = partition(a, l, r);
        quickSort(a, l, pos[0] - 1);
        quickSort(a, pos[1] + 1, r);
    }
}
int * partition(ElementType a[], int l, int r) {
    int small = l - 1, big = r + 1;
    int i = l;
    int chooseIdx = rand()*(r - l + 1) + l;
    ElementType pivot = a[chooseIdx];
    while(i < big) {
        if(a[i] > pivot) {
            swap(a, i, --big);
        } else if(a[i] < pivot) {
            swap(a, i++, ++small);
        } else {
            i++;
        }
    }
    int *pos = new ElementType[2];
    pos[0] = small + 1;
    pos[1] = big - 1;
    return pos;
}


// ----- 8.4.1 选择排序 -----

void selectSort(ElementType a[], int n) {
    if(n < 2) {
        return;
    }
    for(int i = 0; i < n; i++) {
        int min = i;
        for(int j = i + 1; j < n; j++) {
            if(a[j] < a[min]) {
                min = j;
            }
        }
        swap(a, i, min);
    }
}


// ----- 8.4.2 堆排序 -----

void heapInsert(ElementType a[], int i) {
    while(a[i] < a[(i - 1) / 2]) {
        swap(a, i, (i - 1) / 2);
        i = (i - 1) / 2;
    }
}

void heapify(ElementType a[], int len) {
    int p = 0;
    int l = 2 * p + 1;
    int r = l + 1;
    int maxIdx = l;
    while(l < len) {
        if(r < len && a[maxIdx] < a[r]) {
            maxIdx = r;
        }
        if(a[maxIdx] >= a[p]) {
            return;
        }
        swap(a, maxIdx, p);
        p = maxIdx;
        l = 2 * p + 1;
        maxIdx = l;
        r = l + 1;
    }
}

void heapSort(ElementType a[], int n) {
    if(n < 2) return;
    for(int i = 0; i < n; i++) {
        heapInsert(a, i);
    }
    for(int i = n - 1; i >= 0; i--) {
        swap(a, 0, i);
        heapify(a, i);
    }
}


// ----- 8.5.1 归并排序 -----

void merge(ElementType a[], int mid, int st, int en) {
    int n = en - st + 1;
    ElementType *help = (ElementType *)malloc(n * sizeof(ElementType));
    int l = st, r = mid + 1;
    int cnt = 0;
    while(l <= mid && r <= en) {
        if(a[l] <= a[mid]) {
            help[cnt++] = a[l++];
        } else {
            help[cnt++] = a[r++];
        }
    }
    while(l <= mid) {
        help[cnt++] = a[l++];
    }
    while(r <= en) {
        help[cnt++] = a[r++];
    }
    for(int k = 0; k < cnt; k++) {
        a[k + l] = help[k];
    }
}
void mergeSort(ElementType a[], int st, int en) {
    if(st >= en) return;
    int mid = st + (en - st) / 2;
    mergeSort(a, st, mid);
    mergeSort(a, mid + 1, en);
    merge(a, mid, st, en);
}
void mergeSort(ElementType a[], int n) {
    if(n < 2) return;
    mergeSort(a, 0, n - 1);
}

基数排序
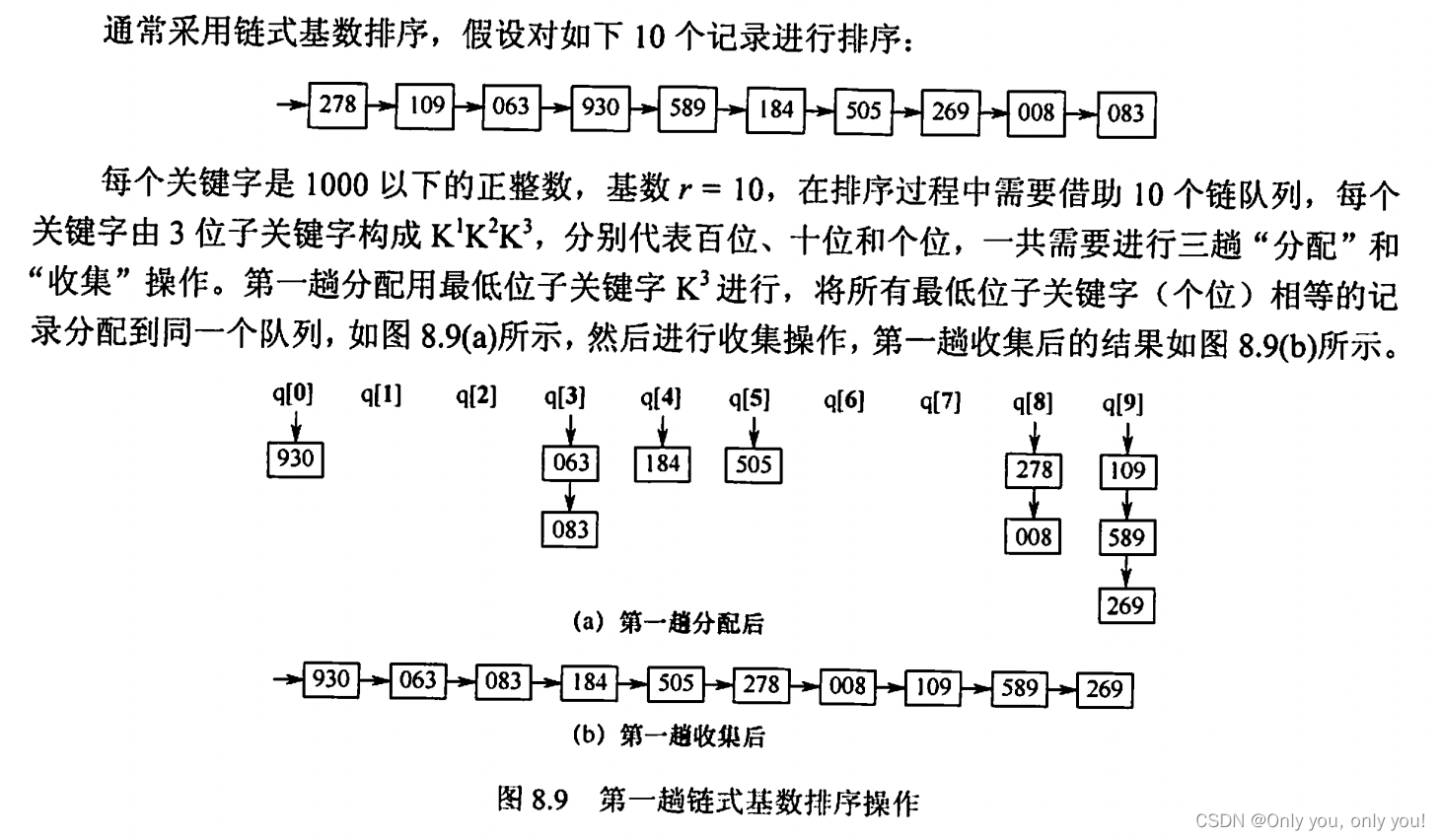
在这里插入图片描述

各种内部排序对比
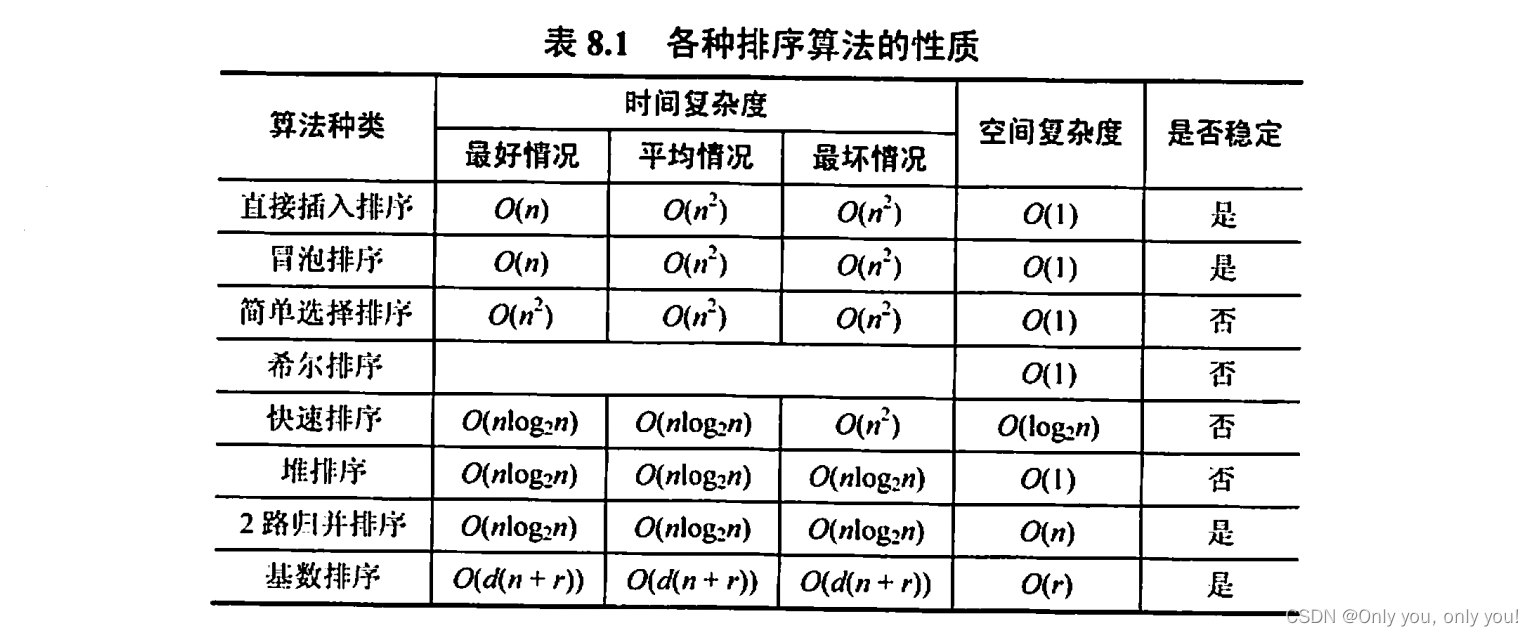
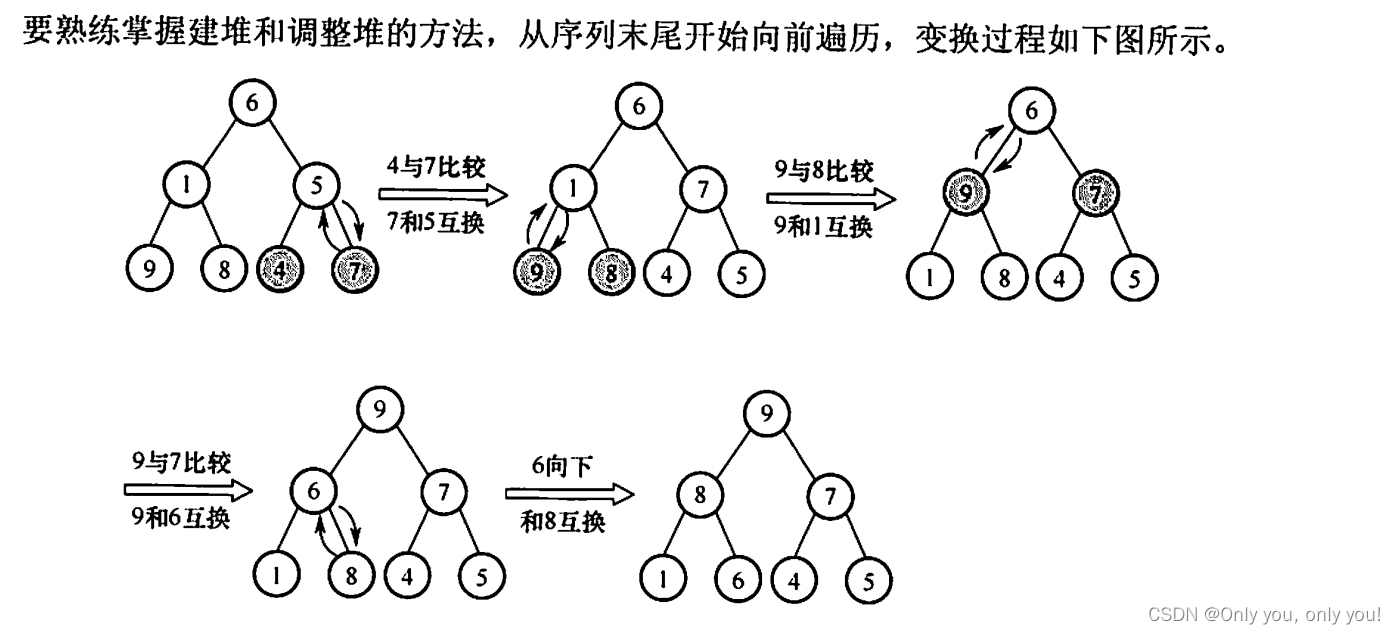
在这里插入图片描述
外部排序

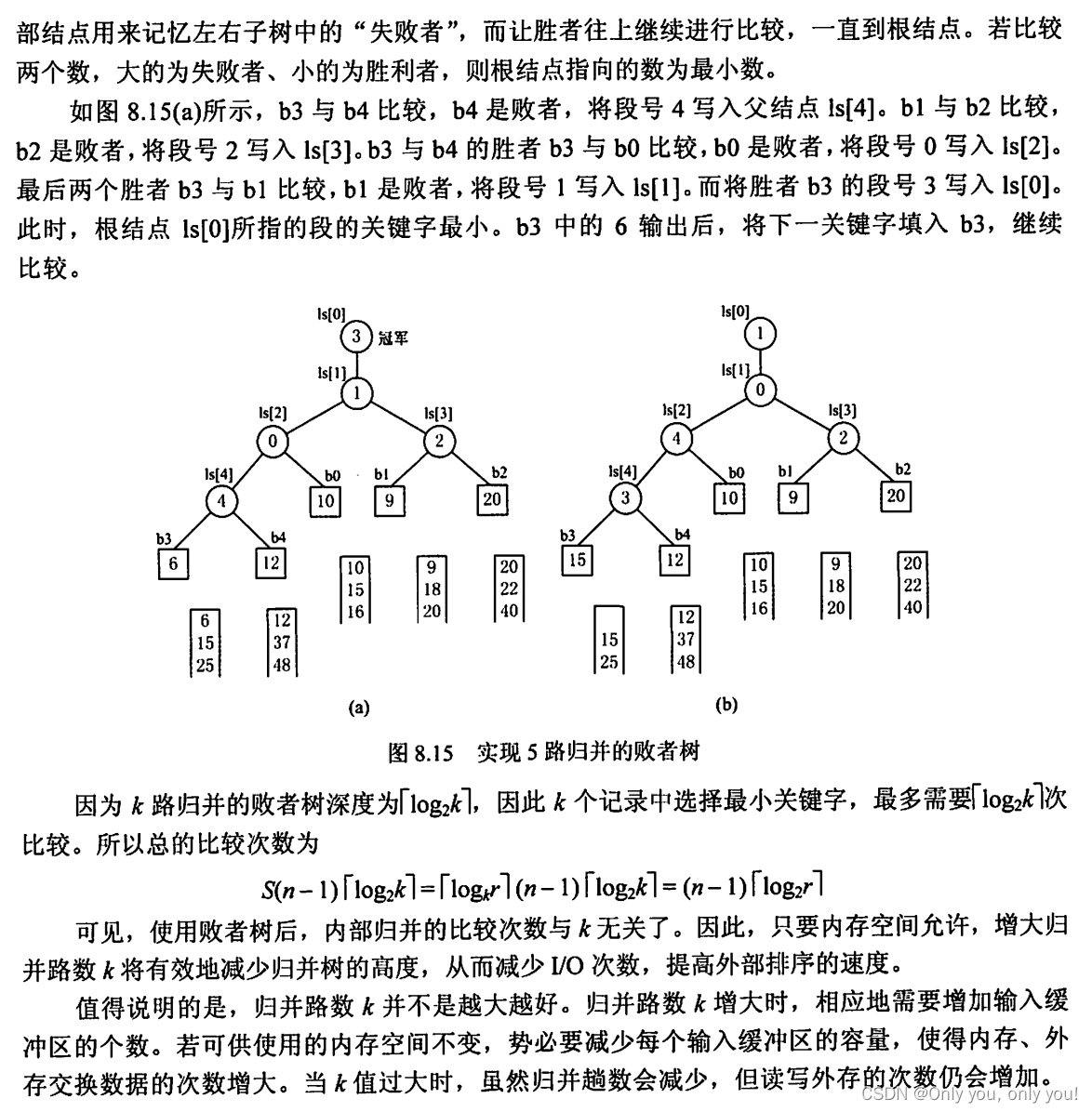
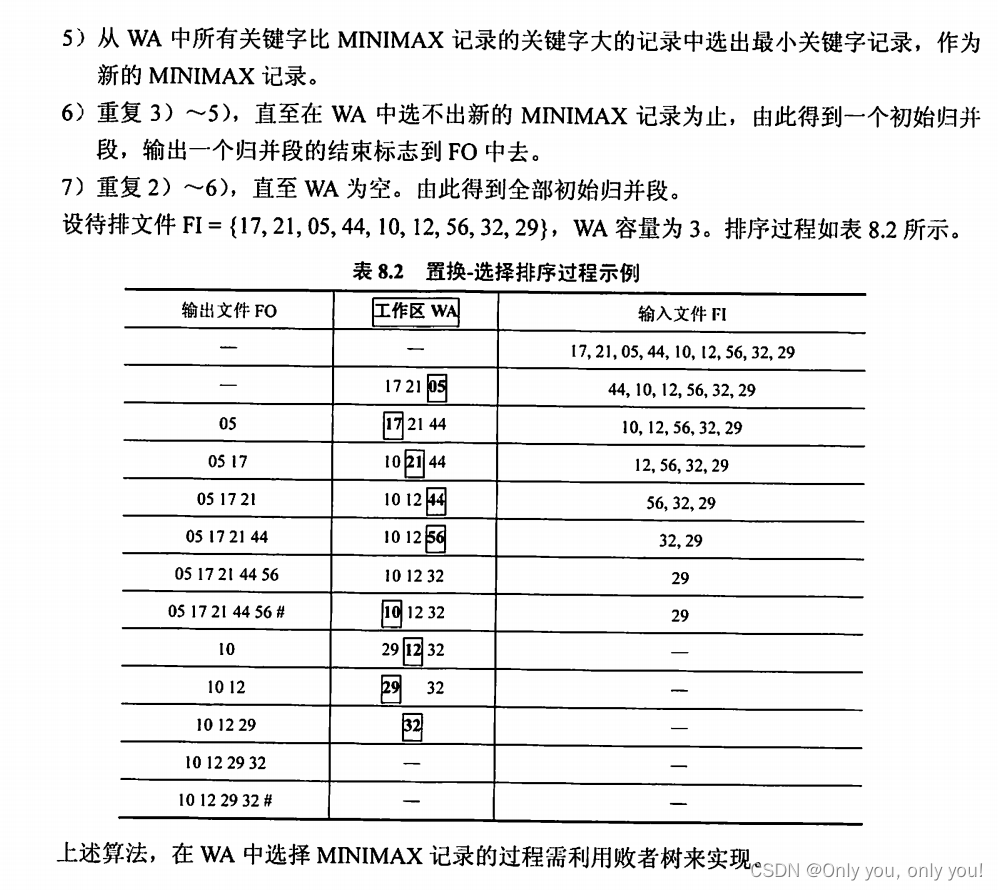
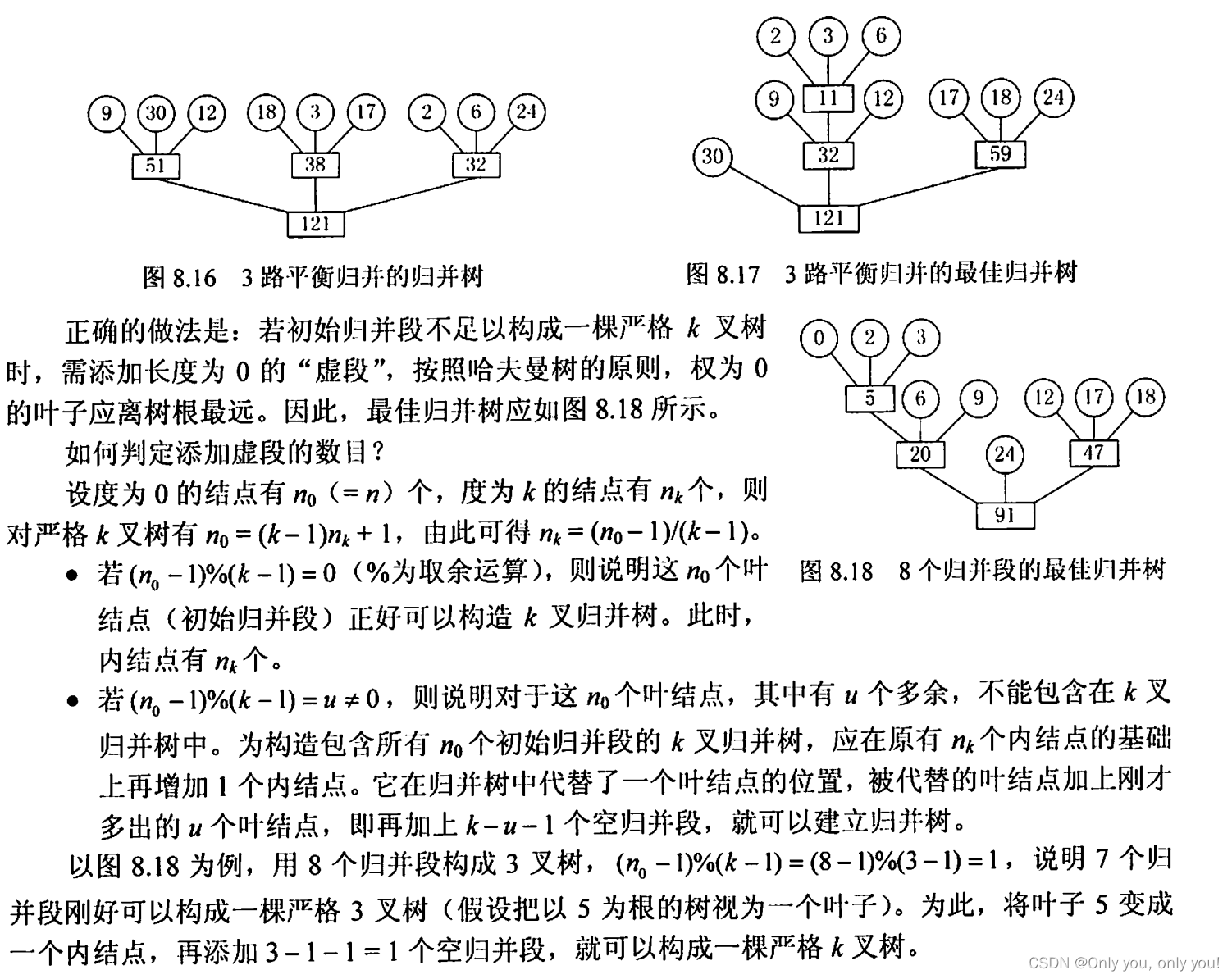
在这里插入图片描述

错题

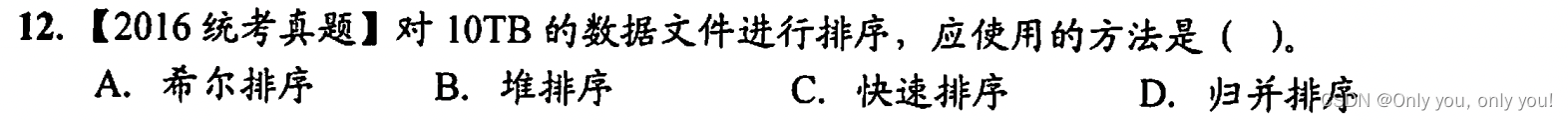
在这里插入图片描述

在这里插入图片描述
解答：显然10TB的数据无法一次存在内存中进行内部排序，只能放在外存中, 排序时将部分数据送入内存进行，显然要用外部排序，而选项中只有归并排序是外部排序。

在这里插入图片描述

C++相关零碎知识点

#include<cstdio>
#include<map>
#include<stack>
#include<queue>
#include<set>
#include<cmath>

#include<iostream>

using namespace std;

void arrayExample();
void mapExample();
void setExample();
void stackExample();
void queueExample();

int main() {
    printf("Hello, World!\n");
    // printf("%ld\n",__cplusplus);

    // arrayExample();
    // mapExample();
    // setExample();
    // stackExample();
    // queueExample();
}

// ----- array ----- 
void arrayExample() {
    int *a = (int *)malloc(sizeof(int) * 10);
    for(int i = 0; i < 10; i++) {
        *(a + i) = i;
    }
    for(int i = 0; i < 10; i++) {
        printf("%d ", *(a + i));
    }
}

// ----- map ----- 
void mapExample() {
    map<int, int> m;
    m[1] = 11;
    m[2] = 22;
    m[3] = 33;
    
    map<int, int> :: iterator it;
    for(it = m.begin(); it != m.end(); it++) {
        int k = (*it).first;
        int v = (*it).second;
        printf("k = %d, v = %d\n", k, v);
    }

    if(m.find(1) != m.end()) {
        printf("1 exists in m.\n");
    }
}

// ----- set ----- 
void setExample() {
    set<int> s;
    for(int i = 0; i < 5; i++) {
        s.insert(i);
    }
    set<int> :: iterator it;
    for(it = s.begin(); it != s.end(); it++) {
        printf("%d ", *it);
    }
    printf("\n");
    
    if(s.find(3) != s.end()) {
        printf("3 exists in s.\n");
    }
}

// ----- stack ----- 
void stackExample() {
    stack<int> s;
    for(int i = 0; i < 5; i++) {
        s.push(i);
        printf("%d ", i);
    }
    printf("\n");
    while(!s.empty()) {
        int top = s.top();
        s.pop();
        printf("%d ", top);
    }
    printf("\n");
}

// ----- queue ----- 
void queueExample() {
    queue<int> q;
    for(int i = 0; i < 5; i++) {
        q.push(i);
        printf("%d ", i);
    }
    printf("\n");
    while(!q.empty()) {
        int front = q.front();
        q.pop();
        printf("%d ", front);
    }
    printf("\n");
}