题目：

给定一个01串（仅由字符'0'和字符'1'构成的字符串）。每次操作可以交换两个相邻的字符。

例如：对于字符串"001110"来说，

可以交换第二个字符'0'和第三个字符'1'，交换之后的字符串变成了"010110"。

如果想要最终字符串任意两个相邻的字符都不相同，最少需要多少操作次数？

保证输入的所有字符串测试用例通过交换后一定能够形成相邻两个字符都不相同的字符串。

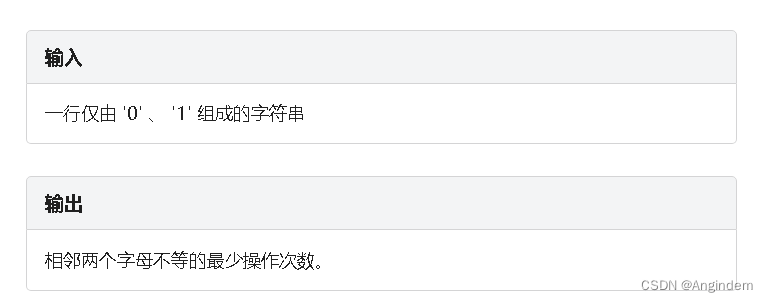
样例：

输入
`11100`

输出
3

思路：

贪心思路，观察01串我们知道，如果要01串相邻字符不相同，那么有两种情况出现。

情况
1、当 0 和 1 个数不相同的时候，我们知道肯定是个数最多的数字作开头，个数最少的操作的时候可能无法达到01串相邻字符不相同 ---------------------------------------------------------------------------------------------- 2、当 0 和 1 个数相同的时候，有可能两个数字都可以作为开头，而我们需要找到最少的操作数

沿着这个思路，我们需要的是操作函数，对于操作的时候，我们应该取最近的不同字符进行交换，所以我们需要一个 pos 来错开一个字符，即 pos += 2，

操作步数：对应需要操作数字的下标 - pos 即： step += abs(i - pos)

代码详解如下：

#include <iostream>
#include <unordered_map>
#define endl '\n'
#define YES puts("YES")
#define NO puts("NO")
#define umap unordered_map
#pragma GCC optimize(3,"Ofast","inline")
#define ___G std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10;

string s;	// 01 串
int len;	// 长度
int ans;	// 答案
inline int swapStep(char c)
{
	// 交换的步数
	int step = 0;
	
	// 交换的最近距离
	int pos = 0;
	
	for(int i = 0;i < len;++i)
	{
		// 从左往右遍历，找到是操作的数字
		if(s[i] == c)
		{
			// 累加交换字符的步数
			step += abs(i - pos);
			
			// 这里是错开一个位置的字符
			// 达到相邻字符不相同，所以 pos += 2;
			// 例如：  11100   
			/* 操作 1 : i = 0 pos = 0 step = 0;
						i = 1 pos = 2 step += abs(i - pos) = 0 + 1;
						i = 2 pos = 4 step += abs(i - pos) = 1 + 2 = 3;
						
			   操作 0 ：i = 3 pos = 0 step = 0;
			   			i = 4 pos = 2 step += abs(i - pos) = 2; 
			   			
				从上面例子模拟，可以知道，0 只需要操作两次，
				即：  11010   第一次
				      11001   第二次
				      
				所以不能变成 相邻不相同
				
				而
				操作 1 的时候：  11010    第一次
							     10110    第二次
								 10101    第三次 
			*/
			pos += 2;
		}
	}
	// 返回操作步数
	return step;
}

inline void solve()
{
	getline(cin,s);
	len = s.size();
	
	int r[2] = {0,0};	// 统计 0 和 1 的个数
	
	for(auto i : s)
	{
		int num = i - '0';
		++r[num];	// 统计 0 和 1 个数
	}
	
	// 取出 0 和 1 的操作步数
	int op0 = swapStep('0');
	int op1 = swapStep('1');
	
	// 如果 0 和 1 的数量相同
	// 说明 0 和 1 都可以做开头
	if(r[0] == r[1])
	{
		// 所以我们取最少的操作数即可
		ans = min(op0,op1);
	}
	else
	{
		// 否则我们应该让 个数 最多的数字开头
		// 所以我们取 个数最多的操作数
		// 因为个数最多，相当于操作最少
		// 为什么不直接取 min (op1,op0)
		// 是因为 当我们个数不相等的时候，个数最少的操作数是不合法了
		// 因为它只进行了一次交换一样达到了相邻字符不相同
		ans = r[0] > r[1] ? op0 : op1;	
	}	
	
	cout << ans << endl;
	
}


int main()
{
//	freopen("a.txt", "r", stdin);
//	___G;
	int _t = 1;
//	cin >> _t;
	while (_t--)
	{
		solve();
	}

	return 0;
}