贪心法

  我在当前情况下，我把我做到最好。我也不管全局如何，整体如何。我就考虑我现在的这一个，或者这一小部分怎样最好。

• 贪心技术是一种设计算法的通用策略。
• 贪心技术的基本思想：
  • 基于贪心选择准则，每次得到局部最优的选择。
  • 希望利用局部最后得到全局最优解。
  • 贪心选择性质：局部最优可以得到全局最优。
• 找到正确的贪心选择准则是设计贪心算法的关键。
  • 不同的贪心选择准则可以得到不同的结果。

打个比方，我现在有几种选择：

学编程、打游戏、读书、去外面玩、去兼职、……

如果我的目的是提高自己的知识水平，那起码对于现在的这些选择来说，我选择“学编程”或者“读书”就是最优的。

只是说当前这一步怎么走是最优的，也并没有去管后面的路怎么走。

比如你说选择“打游戏”，后面可能也会更成功，但是不管这个。

找零问题（change-making problem）

• 给定无限多不同面额的硬币$d_1>...>d_m$，对于总额$n$，如何找到最少的硬币数目？
• 问题：目标函数和约束条件是什么？

例如：

$d_1=25c,d_2=10c,d_3=5c,d_4=1c，而且n=48c$。

我们可能想，要使得硬币数目最少，那简单啊。

先紧着面额最大的来凑就行了。

先拿个25c的、再拿两个10c的，5c的没法拿，于是再拿3个1c的。

于是得到贪婪解：<1,2,0,3>。

我们这个策略就是，很简单，先紧着最大的拿。

但是我们虽然这样做了，而且貌似可行。

但是实际上，它对于大多数情况而言，这样可能是没问题的；但是没法保证所有情况啊，你没法保证对于所有情况、任意某一种情况，这样都没问题。

有一些情况，你这样做，可能就压根不是最优解了。

但是：

• 对大多数常用的硬币面额都可以得到最优解。
• 对任意硬币面额，有可能不是最优解。

例如：

$d_1=25c,d_2=10c,d_3=1c而且n=30c$。

那么你还按照上面的规则，

先拿个25c的，然后拿五个1c的。——此时是6个硬币。

但实际上我们可以看出，直接拿三个10c的就够了，而且只用3个硬币。

所以可见，我们刚才的那种简单的想法：先紧着大面额的拿。

这种方法，可能在某些情况下没毛病，但是在有些情况下就不对了、不是最优解了。

**那咋办呢。**是不是我的想法、我的策略设计的有问题呢？

那到底咋样弄，才能对于所有情况都能得到最优解呢？

我们可以用回溯法。（不是讲贪心吗，咋又说回溯了？——后面再说这个问题）

---

• **贪婪法：**建议通过一系列步骤来构造问题的解，每一步对目前构造的部分解做一个扩展，直到获得问题的完全解。（完全解，不是最优解）
• 必须满足：可行、局部最优、不可取消。

贪心算法要求

• 可行的：即它必须满足问题的约束。
• 局部最优：它是当前步骤中所有可行选择中最佳的局部选择。
• 不可取消：即选择一旦做出，在算法的后面步骤中就无法改变了。

就像人生中的一些选择一样，就是贪心算法么，每次选的是局部最优，而且选了之后就没法取消了。

  在每一步中，它要求“贪婪”地选择最佳操作，并希望通过一系列局部的最优选择，能够产生一个整个问题的（全局的）最优解。

基本思想

• 从问题的某一个初始解出发，通过一系列的贪心选择（当前状态下的局部最优选择），逐步逼近给定的目标，尽可能快地求得更好的解。
• 在贪心算法（greedy method）中也采用逐步构造最优解的方法。在每个阶段，都做出一个按某个评价函数最优的决策，该评价函数最优称为贪心准则（greedy criterion）。
• 贪心算法的正确性，就是要证明按贪心准则求得的解是全局最优解。
• 贪心算法不能对所有问题都得到全局最优解。
• 但是对于许多问题，它能够产生全局最优解。如单源最短路径问题，最小生成树问题等。

适合求解问题的特征

• **贪心选择性质：**可通过局部最优（贪心）选择达到全局最优解。
  • 通常以自顶向下的方式进行，每次选择后将问题转化为规模更小的子问题。
  • 该性质是贪心法使用成功的保障，否则得到的是近优解。
• 最优子结构性质：问题的最优解包含它的子问题的最优解。
  • 并不是所有具有最优子结构性质的问题都可以采用贪心策略。
  • 往往可以利用最优子结构性质来证明贪心选择性质。

背包问题

• 0-1背包问题

  给定n种物品和一个背包。物品i的重量是$W_i$，其价值为$V_i$，背包的容量为C。应如何选择装入背包的物品，使得装入背包中物品的总价值最大？

0-1背包问题，对于一个物品，0就是不拿它，1就是拿它。

在选择装入背包的物品时，对每种物品只有两种选择，要么装入背包、要么不装入背包。不能将一个物品装入背包多次，也不能只装入某物品的一部分。

• 背包问题

  与0-1背包问题类似，所不同的是，在选择物品i装入背包时，可以选择物品i的一部分，而不一定要全部装入背包，1≤i≤n。

背包问题，也叫“分数背包问题”，对于一个物品，物品太大了，背包剩余空间不够了，此时我可以把物品拆下来、把一部分放进去。

0/1背包问题

• 已知
  • 背包容量C>0
  • n个物品，体积$w_i>0$，价值$p_i>0fori=1,...,n$
• 确定 { 1 , 2 , . . . , n } \{1,2,...,n\} {1,2,...,n}的子集，满足：

$$max\sum _{i\in A}{p}_i,subjectto\sum _{i\in A}{w}_i\le C$$

0/1背包问题——贪心法

• 有以下几种贪心选择准则：

  • 最大价值优先——先选择最值钱的物品。

  紧着最值钱的先往上放。

  • 最小体积优先

  紧着最小体积的先放，想装的多。

  • 最大体积优先

  想着一般大的东西都比较值钱？所以先紧着大件先放？

  • 最大单位价值优先

这四个规则都有一定道理，那我们该选哪种呢？选最大价值优先？选最大单位价值优先？

• 没有一种方法能保证得到最优解

最大价值优先

（lb是重量单位，上面是价钱）

可见，最大价值优先，放进来的不一定是最优解。

最小体积优先

可见，最小体积优先，放进来的也不一定是最优解。

最大体积优先

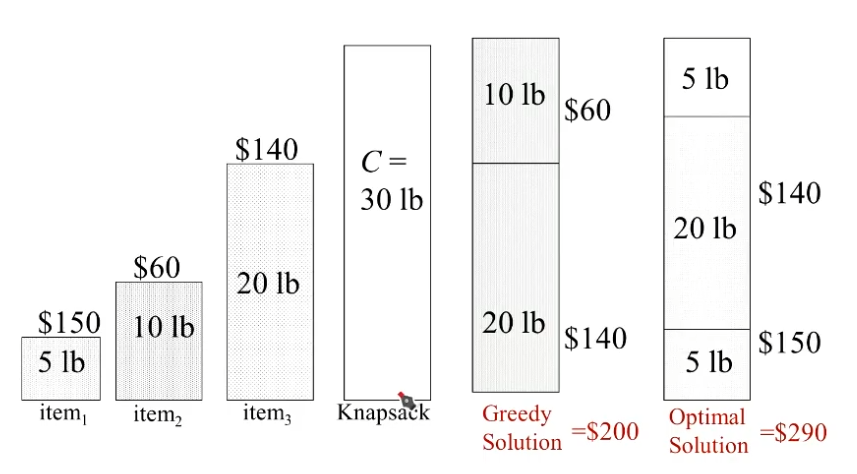
可见，最大体积优先得到的也不一定是最优解。

最大单位价值优先

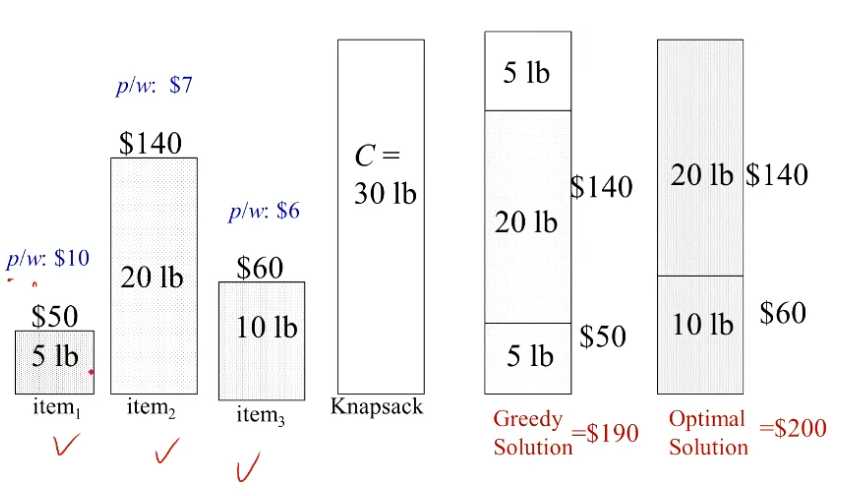
可见，这个也不一定能得到最优解。

---

分数背包问题

• 对于0/1背包问题，没有最优的贪心算法。
• 分数背包问题：可以将第i个物品的一部分放入背包。
• 对于分数背包问题，贪心算法是其不二选择，该算法基于最大单位价值的选择准则。（感觉有点类似于微积分里的微元思想）

这个就没啥好犹豫的了，我先紧着最大单位价值的往里面放，放不下整个物品的时候，我把当前最大单位价值的物品切出来一块往里面放。

这样最后包里放的肯定是价值最大的情况。

• 贪心算法过程：
  • 降序排序$v_i/w_i$。
  • 根据排序次序增加物品，直到这个物品装完，或是超出背包容量。
  • 如果背包没有满，选择下一个物品开始装。

最优解证明

• 证明：

  我们首先假设我们有一个最优解$A_1$，那么我们首先找到$A_1$里面平均价值最高的物品$a_m$，然后我们将用商品里面平均价值最高的物品$a_1$将$a_m$进行全部替换或者部分替换得到解$A_2$，又因为$\frac{v_1}{w_1}\ge \frac{v_m}{w_m}$，所以$A_2$的总价值高于$A_1$的总价值，这与$A_1$是最优解矛盾，于是得到$A_1$里面包含平均价值最高的物品。

---

• 小数背包问题还具有贪心选择性质，用贪心法求解更简单、更快速。
• 0-1背包问题用贪心法求解不一定能得到最优解。

任务调度问题

• 9个任务需要调度，每个任务运行时间为3,5,6,10,11,14,15,18,20

如果只有一个处理器，那就没啥说的，每个任务看看按照什么规则往里放就行了，反正最后总时间是一样的。

但是如果有多个处理器呢？

• 有三个处理器执行这些任务。

当然，对于贪心而言，我们对这一问题也可以有很多种贪心策略。

• 贪心准则：先运行时间最长的任务。

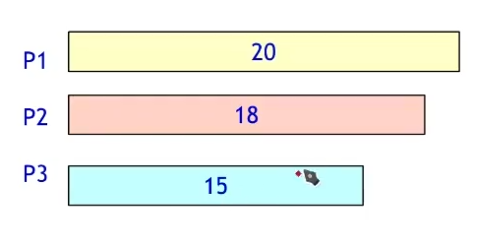
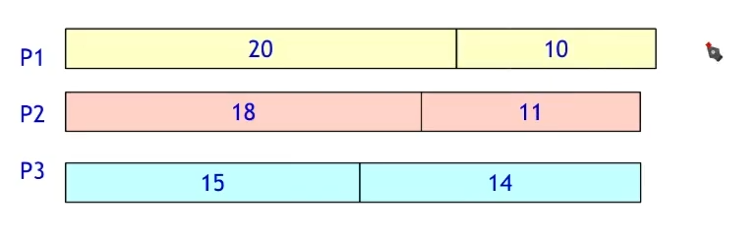
每次把当前需要运行最长时间的任务，分配给当前任务时间最短的处理器。

因此，三个处理器执行这些任务，花费35分钟时间。

这个解决方法不错，但是我们可能还可以有更好的策略。

• 另一种贪心准则：优先运行最短任务

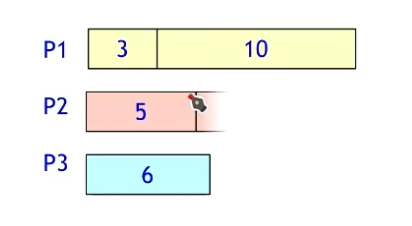
这个方式还不如刚才那个，这个需要花费40分钟。

最优解

折腾半天都不是最好的，那我们看看最优解到底是什么样的，如上图所示。

• 这个解为什么是最优的？

很明显么。因为三个处理器刚好平均分了所有任务的总时长，没有任何的浪费。

  但是，可见，若想得到这样的一种解。你要付出的代价就会很高了。

  有必要么，实际解决一个问题来说，这样去搞，可能没这个必要。你找到最优解了之后，最优解固然能够帮你节约时间；但是不要忽视了，你寻找这个最优解也要花时间。你为了找一个最优解去节约那一点点时间，然后你花了大量的时间在寻找到最优解上，得不偿失。

类似上图中这个最优解，是咋找到的？可能是暴力穷举吧，或者是什么方法。总之很耗时间才能找出来的。

  实际上我就用一种贪心策略，去做，就拉倒了。虽然可能不是最优，但是接近最优差不多就行了。

  对于一些特殊的问题，贪心算法能直接找出其最优解，能直接获取最优解那当然更好了。

  总之贪心算法可能找到的不是最优解，而只是局部最优解；但是它的实现是很简单的，不会耗费太多时间。

---

  同时，我们在贪心，贪的过程中，也可以利用回溯法的思想，对一些没必要继续探讨下去的情况进行剪枝，而没必要全部贪到底、再去排除。也就是贪心法配合回溯法进行使用。

活动选择问题

• 这个就是活动选择问题。

我选择哪些活动，能够让活动数量最多？

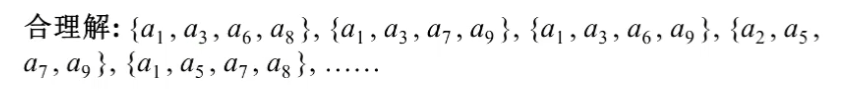
活动选择——贪心法

• 贪心法选择准则：
  • 最早开始时间优先
  • 最小持续时间优先
  • 最早完成时间优先
• 哪个准则更有效？

最早开始时间优先。

假设有一个从0开始的活动，但是它持续时间巨长。

那这显然不是最优解。

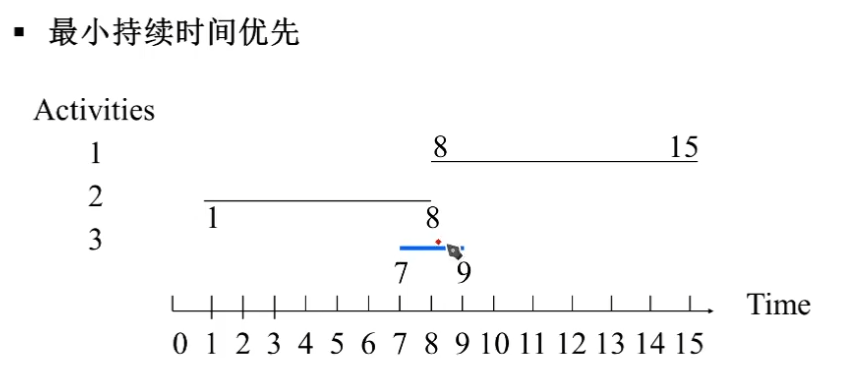
如上图。

这个持续时间最小，但是可能因为做了它，它刚好介于两个活动邻接点，导致两个活动都没法做。

显然也不是最优解。

最早结束时间是不是能达到这个问题的最优解？

实际上，按最早结束时间优先，基本上都能取到最优解。

怎么证明这种策略的正确性？怎么知道上面的例子不是它的特例？

• 需要证明贪心法的正确性。

最早结束时间优先——最优性证明

**定理：**如果活动$a_1$在所有活动中具有最早结束时间，则最优解中一定包含$a_1$。

证明：

• 令$A$是最优解，$a_1$是贪心法选择的最早结束时间的活动。如果$a_1\in A$，则定理得证。
• 如果$a_1\notin A$，我们证明 A ∗ = A − { a } + { a 1 } A^*=A-\{a\}+\{a_1\} A∗=A−{a}+{a1​}是另一个包含$a_1$的最优解，而$a$是$A$中具有最早结束时间的活动。
• 因为活动的结束时间已排序好，$f(a_1)\le f(a)$。假设$f(a_1)\le s(a)$，如果我们把$a_1$加到$A$，意味着$A$不是最优的。所以$s(a)<f(a_1)$，并且$a_1$和$a$重叠。因为$f(a_1)\le f(a)$，如果我们移除$a$添加$a_1$，可以得到另一个最优解$A^{\ast }$包含了$a_1$。$A^{\ast }$是最优的，因为$|A^{\ast }|=|A|$。

没太看懂。

**定理：**贪心子选择一定产生最优解。

即，证明去掉一个$a_1$之后，对剩下的活动做最早结束时间优先策略，得到的也是子集的最优解。

证明：

• 令$a_1$是贪心算法选择的活动。
• 令$S^{\ast }$是不与$a_1$重叠的活动子集

S ∗ = { a i ∣ i = 2 , . . . , n   a n d   s i ≥ f ( a 1 ) } S^*=\{a_i | i=2,...,n\ and\ s_i≥f(a_1)\} S∗={ai​∣i=2,...,n and si​≥f(a1​)}

• 令$B$是$S^{\ast }$的最优解。

• 从$S^{\ast }$的定义可知， A ∗ = { a 1 } ∪ B A^*=\{a_1\}∪B A∗={a1​}∪B是可行的，并且是原问题的解。

• 利用反证法证明$A^{\ast }$是最优解。

• 假设$A^{\ast }$不是最优解，令$A$是包含$a_1$的最优解，则$|A^{\ast }|<|A|$，且 ∣ A − { a 1 } ∣ > ∣ A ∗ − { a 1 } ∣ = ∣ B ∣ |A-\{a_1\}|>|A^*-\{a_1\}|=|B| ∣A−{a1​}∣>∣A∗−{a1​}∣=∣B∣。

• 但是 A − { a 1 } A-\{a_1\} A−{a1​}也是$S^{\ast }$的解，与$B$是$S^{\ast }$的最优解矛盾。

• 所以$A^{\ast }$一定是原问题的最优解。

---

Prim算法

• 连通图的一棵生成树是包含图的所有定点的连通无环子图（一棵树）。
• 加权连通图的一棵最小生成树是图的一棵权重最小的生成树。

  从某个点出发，首先找和它相邻连接的结点中，权值最小的是谁。是b结点、权值为4，那就把b结点并入进来。接着，再找下一条边，就找和a、b相邻的结点中，权值最小的是哪个边，并且把那个结点并入进来。

  总之，可以视作两个集合：一个是已并入最小生成树的结点集合，另一个是还未并入的结点集合。每次找这两个集合之间权值最小的连接（不能形成环）。

---

问题：

  一个图，按照这种方式，找出来的所有的最小生成树是不是都是一样的？

  它是一棵树，树的结构是由什么决定的？——我每次的起始点选取不同，它的树根结点不一样，肯定就不一样了。

---

总结

  贪心策略的选择很重要。

  贪心在某些情况下是可以拿到最优的，但是很容易得到一个局部最优而非全局最优的解。