状态机简介：

1.大盗阿福

阿福是一名经验丰富的大盗。趁着月黑风高，阿福打算今晚洗劫一条街上的店铺。

这条街上一共有 $N$家店铺，每家店中都有一些现金。

阿福事先调查得知，只有当他同时洗劫了两家相邻的店铺时，街上的报警系统才会启动，然后警察就会蜂拥而至。

作为一向谨慎作案的大盗，阿福不愿意冒着被警察追捕的风险行窃。

他想知道，在不惊动警察的情况下，他今晚最多可以得到多少现金？

输入格式
输入的第一行是一个整数 $T$，表示一共有$T$组数据。

接下来的每组数据，第一行是一个整数 $N$，表示一共有$N$家店铺。

第二行是$N$个被空格分开的正整数，表示每一家店铺中的现金数量。

每家店铺中的现金数量均不超过$1000$。

输出格式
对于每组数据，输出一行。

该行包含一个整数，表示阿福在不惊动警察的情况下可以得到的现金数量。

数据范围
$1\le T\le 50,$
$1\le N\le 10^5$

输入样例：

2
3
1 8 2
4
10 7 6 14

输出样例：

8
24

样例解释
对于第一组样例，阿福选择第2家店铺行窃，获得的现金数量为$8$。

对于第二组样例，阿福选择第1和4家店铺行窃，获得的现金数量为$10+14=24$。

1.1题解

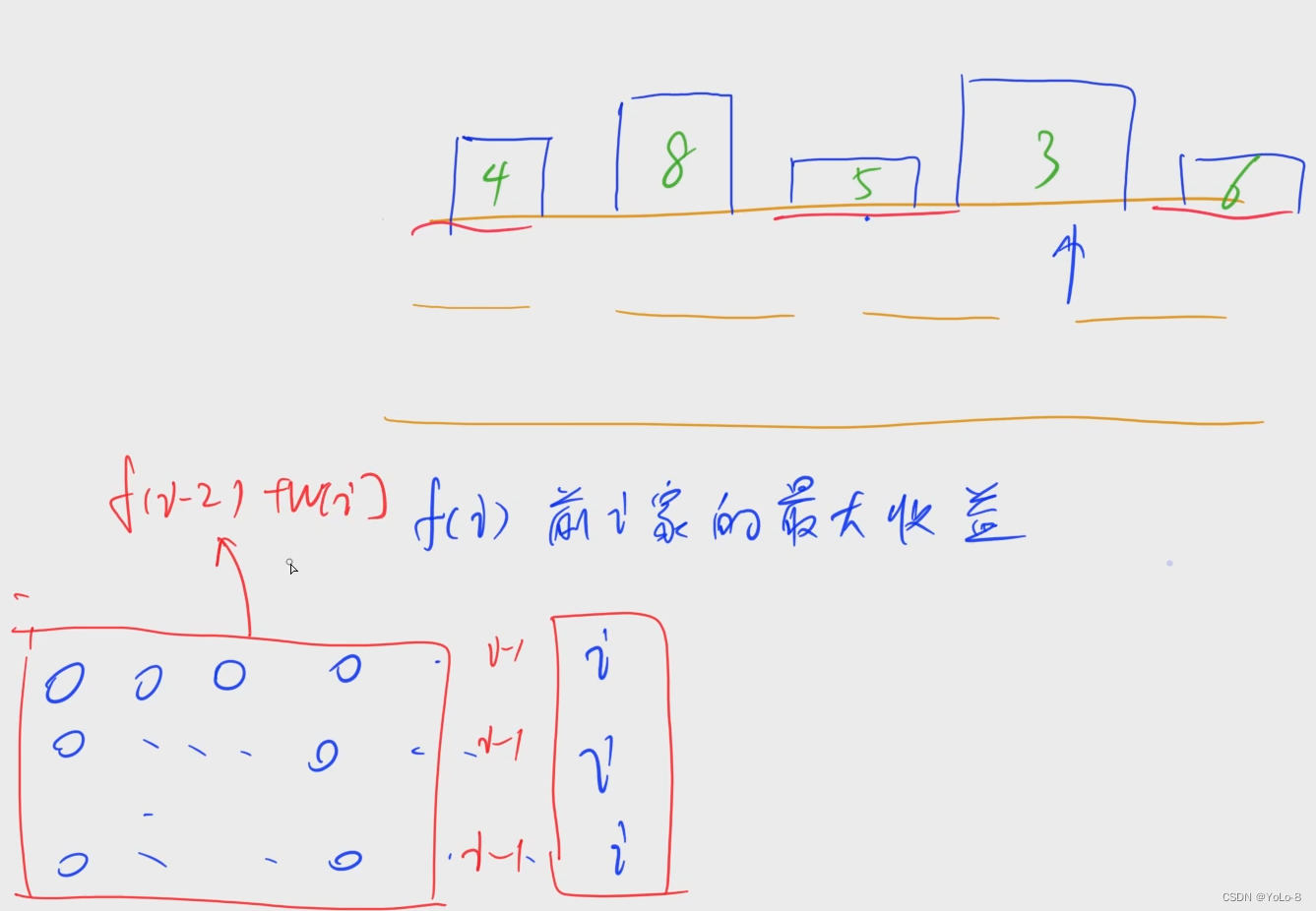
现在考虑只从上一层状态，而不是从上两层状态

分解状态

状态机模型

利用DP分析法+状态机

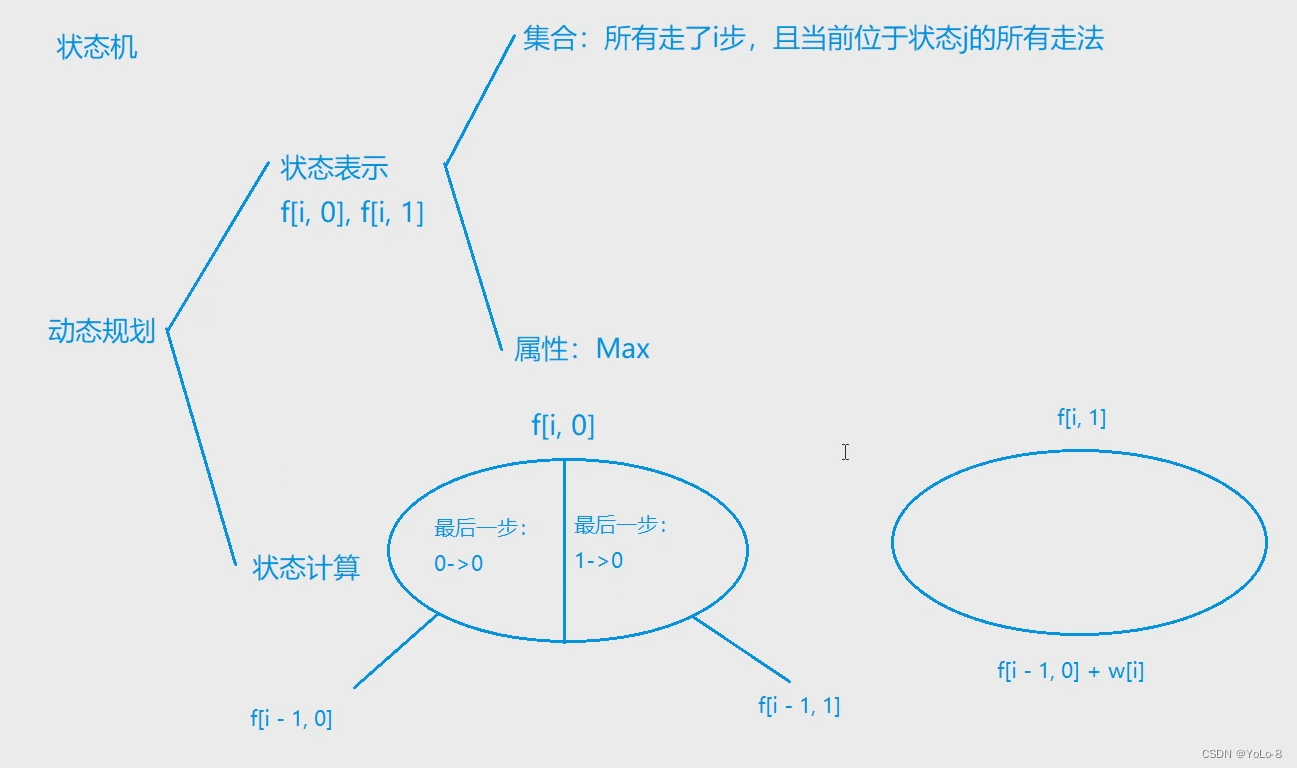
利用状态机的形式把不好表示的状态分离开

思路1
我们可以定义一个数组，为$f[]$

$f[i]$表示抢劫前i家能得到的最多现金数量。

那么我们前i家的抢劫结果就有两种情况：

第一种情况：不偷第i家店铺
那么$f[i]=f[i-1]$;

第二种情况：偷第i家店铺
那么$f[i]=f[i-1]+w[i].$

$w[i]$表示第i家店铺总共的现金)

思路1出现的问题：
如果第$i-1$家店已经被抢了，那么如果抢了第$i$家，那是不符合题目要求的。

那怎么办呢？

正确方法(思路2)：

我们把f数组定为二维的，即$f[][]$

我们用数组储存两种情况：偷与不偷。

$f[i][0]$代表的是不偷第i家店铺能得到的最多现金数量；
$f[i][1]$代表的是偷第i家店铺能得到的最多现金数量。

则就会出现三种情况：

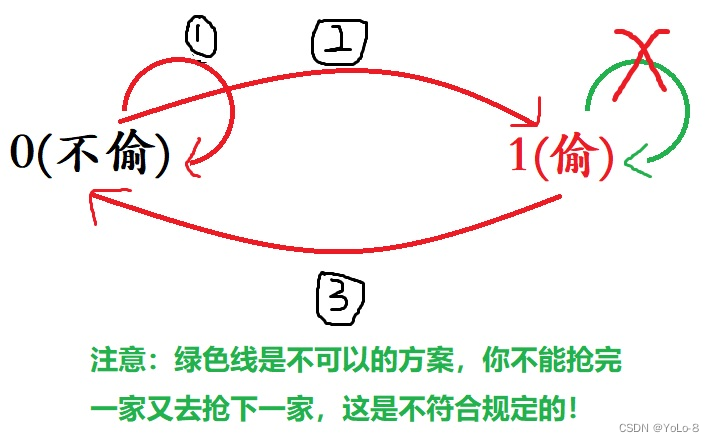
解释：

图中红色的线是可行方案，你可以不抢第$i-1$家，也不抢第$i$家；
你可以不抢第$i-1$家，但抢第$i$家。
你可以抢第$i-1$家，但不抢第$i$家；

那么我们就可以得出状态转移方程了：

f[i][0] = max(f[i - 1][0], f[i - 1][1]);
f[i][1] = f[i - 1][0] + w[i];

1.2代码实现

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 100010,INF = 0x3f3f3f3f;
int n;
int w[N],f[N][2];

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        for(int i = 1;i <= n;i++)   scanf("%d",&w[i]);
        f[0][0] = 0,f[0][1] = -INF;
        for(int i = 1;i <= n;i++)
        {
            f[i][0] = max(f[i - 1][0],f[i - 1][1]);
            f[i][1] = f[i - 1][0] + w[i];
        }
        printf("%d\n",max(f[n][0],f[n][1]));
    }
    
    return 0;
}

2.股票买卖 IV

给定一个长度为$N$的数组，数组中的第$i$个数字表示一个给定股票在第$i$天的价格。

设计一个算法来计算你所能获取的最大利润，你最多可以完成$k$笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。一次买入卖出合为一笔交易。

输入格式
第一行包含整数$N$和$k$，表示数组的长度以及你可以完成的最大交易笔数。

第二行包含$N$个不超过$10000$的正整数，表示完整的数组。

输出格式
输出一个整数，表示最大利润。

数据范围
$1\le N\le 10^5,$
$1\le k\le 100$
输入样例1：

3 2
2 4 1

输出样例1：

2

输入样例2：

6 2
3 2 6 5 0 3

输出样例2：

7

样例解释
样例1：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

样例2：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。共计利润 4+3 = 7.

2.1题解

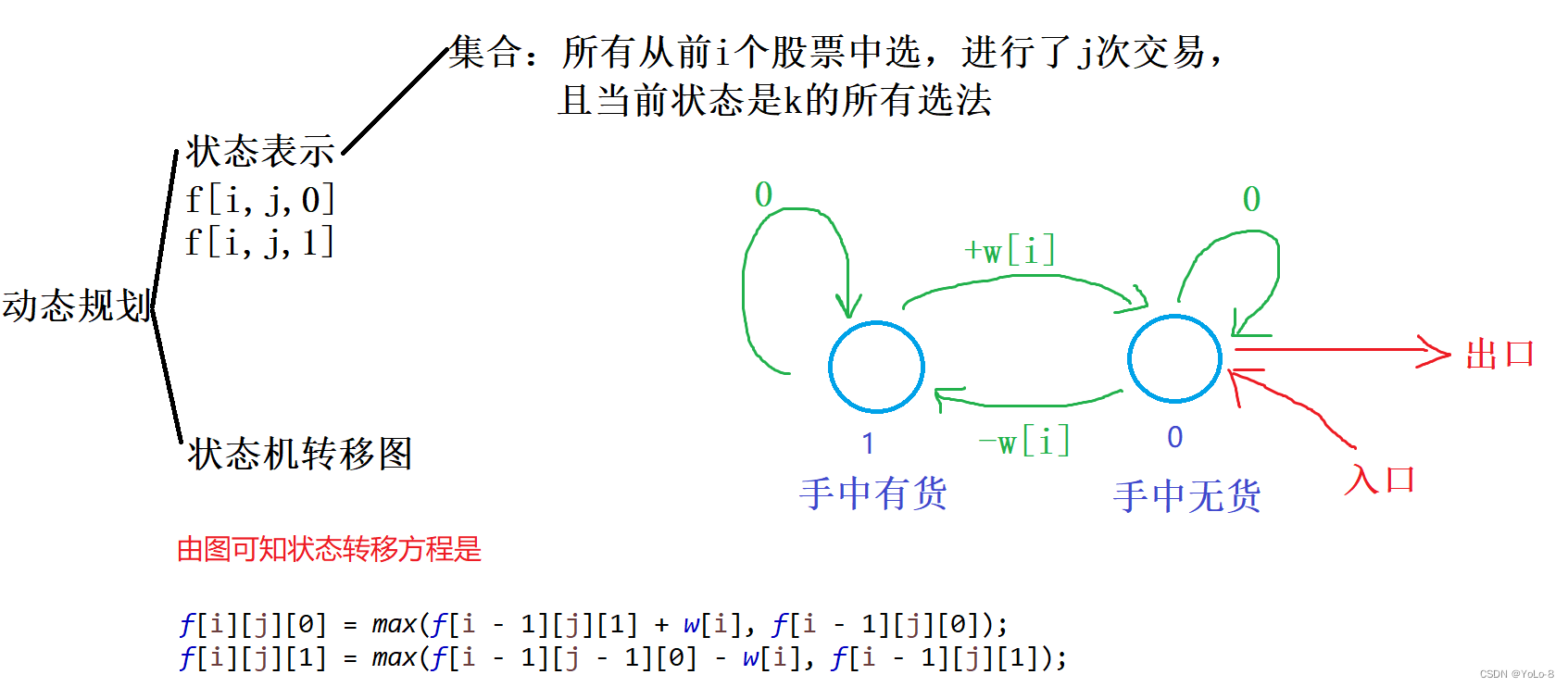
初始化：f[0][j][0] = 0, 其余-INF，因为在第0个股票一定是无货的，必定从这个位置开始转移才有效

注意：
这里状态机的过程，对于每个股票，要么就买，要么就卖，不能说是买了然后在同一个点直接卖掉，这样是不符合状态机模型的，因此对于上述转移方程可以会有人提出疑问。
为什么状态转移方程不能是下面代码，即卖的时候才算做了一次交易，原代码是买的时候才算一次交易

f[i][j][0] = max(f[i - 1][j - 1][1] + w[i], f[i - 1][j][0]);
f[i][j][1] = max(f[i - 1][j][0] - w[i], f[i - 1][j][1]);

终究要回归到状态转移的起点，第一支股票只有买，和不买这两个操作，一定不可能是卖和不卖的这两个操作，因此第一支股票如果买入时，必须按照一次交易处理。否则如果第一次股票如果买入时，不按一次交易处理，也就代表着第一支股票卖出才算一次交易，也就代表着在第一支股票卖出之前还买了一支股票，显然是矛盾的。

2.2代码实现

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 100010,M = 110,INF = 0x3f3f3f3f;

int n,m;
int w[N];
int f[N][M][2];//状态

int main()
{
    scanf("%d%d",&n,&m);
    for(int i = 1;i <= n;i++)   scanf("%d",&w[i]);   
    
    memset(f,-0x3f,sizeof f);
    for(int i = 0;i <= n;i++)    f[i][0][0] = 0;
   
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= m;j++)
        {
            f[i][j][0] = max(f[i - 1][j][0],f[i - 1][j][1] + w[i]);
            f[i][j][1] = max(f[i - 1][j][1],f[i - 1][j - 1][0] - w[i]);
        }
    
    //枚举一下进行多少次交易
    int res = 0;
    //最后手中一定没货
    for(int i = 0;i <= m;i++)   res = max(res,f[n][i][0]);
    printf("%d",res);
    return 0;
}

3.股票买卖 V

给定一个长度为$N$的数组，数组中的第$i$个数字表示一个给定股票在第$i$天的价格。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

• 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
• 卖出股票后，你无法在第二天买入股票 (即冷冻期为 1天)。

输入格式
第一行包含整数$N$，表示数组长度。

第二行包含$N$个不超过$10000$的正整数，表示完整的数组。

输出格式
输出一个整数，表示最大利润。

数据范围
$1\le N\le 10^5$
输入样例：

5
1 2 3 0 2

输出样例：

3

样例解释
对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]，第一笔交易可得利润 $2-1=1$，第二笔交易可得利润 $2-0=2$，共得利润 $1+2=3$。

3.1题解

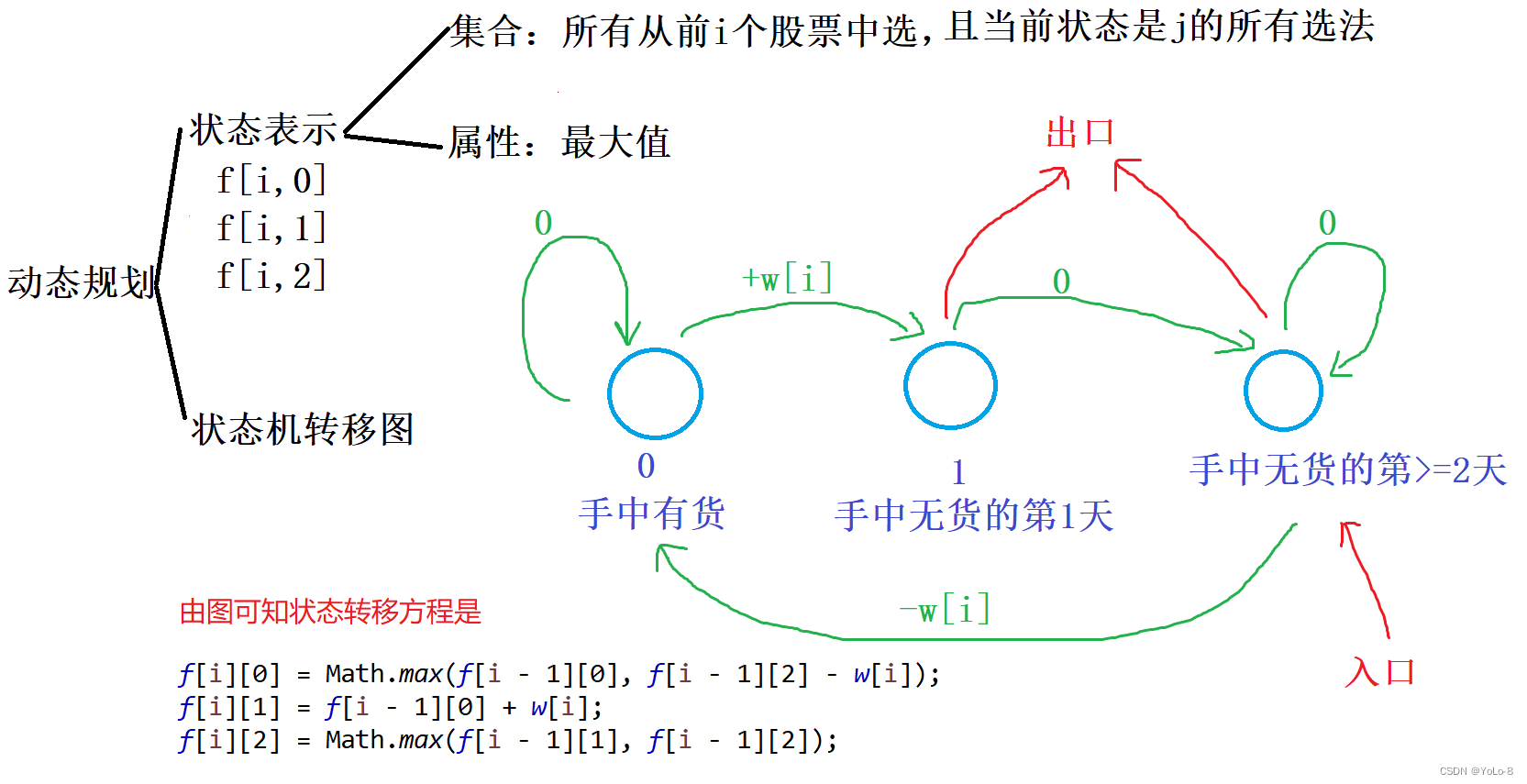
初始化：f[0][2] = f[0][1] = 0，f[0][0] = -INF， 因为在第0个股票一定是无货的，必定从这个位置开始转移才有效

3.2代码实现

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 100010,INF = 0x3f3f3f3f;

int n;
int w[N];
int f[N][3];

int main()
{
    scanf("%d",&n);
    for(int i = 1;i <= n;i++)   scanf("%d",&w[i]);
    f[0][0]  = - INF;
    f[0][2] = f[0][1] = 0;
    
    for(int i = 1;i <= n;i++)
    {
        f[i][0] = max(f[i - 1][0],f[i - 1][2] - w[i]);
        f[i][1] = f[i - 1][0] + w[i];
        f[i][2] = max(f[i - 1][1],f[i - 1][2]);
    }
    
    cout << max(f[n][1],f[n][2]) <<endl;
    
    return 0;
}

4.设计密码

你现在需要设计一个密码$S$，$S$需要满足：

$S$的长度是$N$；
$S$只包含小写英文字母；
$S$不包含子串 $T$；
例如:$abc$和 $abcde$是 $abcde$的子串，$abd$不是 $abcde$的子串。

请问共有多少种不同的密码满足要求？

由于答案会非常大，请输出答案模 $10^9+7$的余数。

输入格式
第一行输入整数$N$，表示密码的长度。

第二行输入字符串$T$，$T$中只包含小写字母。

输出格式
输出一个正整数，表示总方案数模 $10^9+7$后的结果。

数据范围
$1\le N\le 50,$
$1\le |T|\le N，|T|$是$T$的长度。

输入样例1：

2
a

输出样例1：

625

输入样例2：

4
cbc

输出样例2：

456924

4.1题解（此题较为麻烦，融合了自动机和KMP）

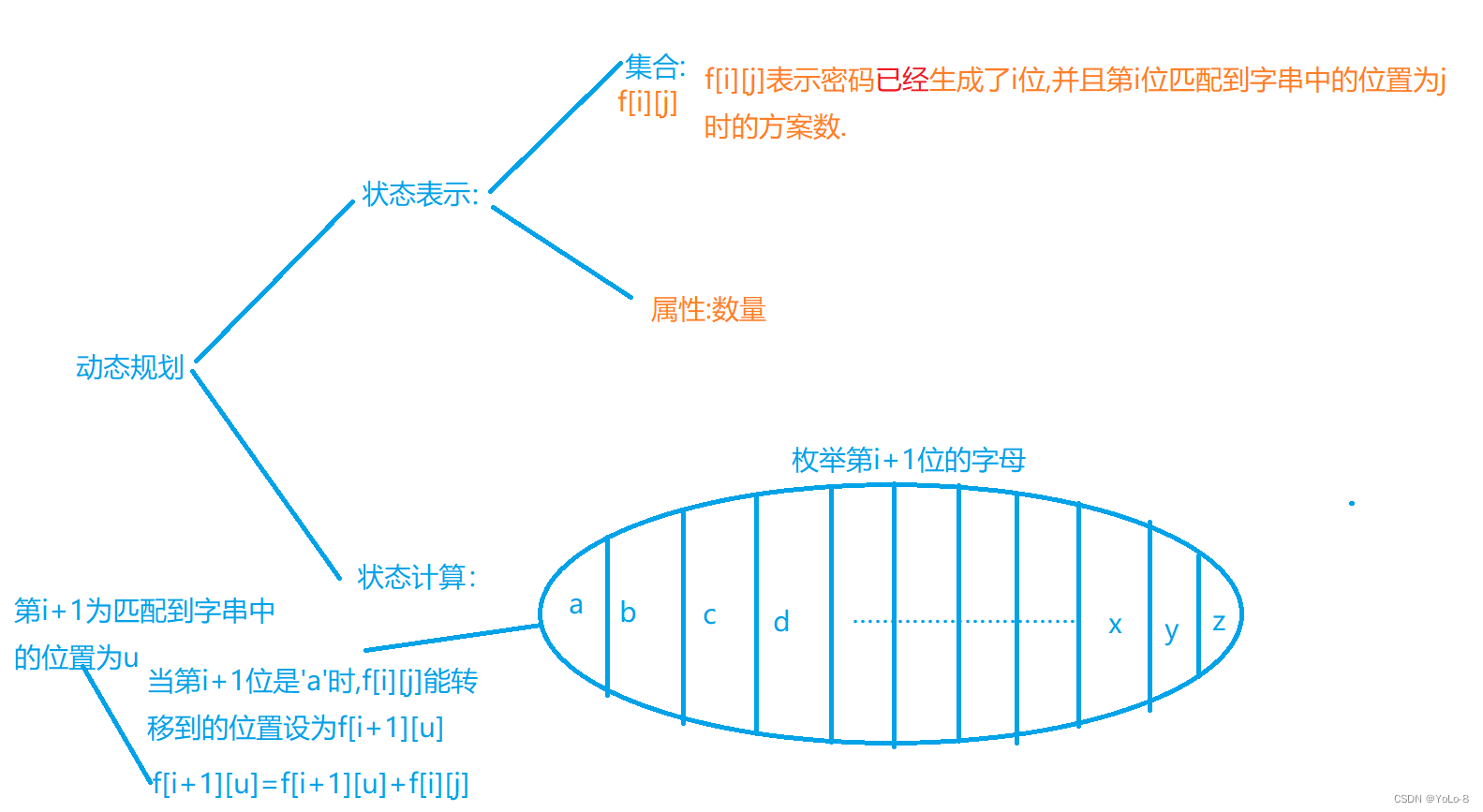
为什么这样的状态表示是可行的呢?
因为$S$数组中的第$n$位有$26$个小写字母,匹配在$T$中的位置一定存在(因为不匹配,匹配到的位置是$0$),
所以把所有$f[n][0m-1]$加起来即为总方案数

4.2代码实现

#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N=55,mod=1e9+7;

int f[N][N],ne[N];
char str[N];//子串

int main()
{
    int n,m;
    cin>>n>>str+1;
    m=strlen(str+1);

    for(int i=2,j=0;i<=m;i++)//求出ne数组(kmp模板)
    {
        while(j&&str[j+1]!=str[i]) j=ne[j];
        if(str[j+1]==str[i]) j++;
        ne[i]=j;
    }

    f[0][0]=1;//已经匹配了0位,且匹配的子串的位置是0时的方案数为1;(初始化)
    for(int i=0;i<n;i++)//枚举密码位
     for(int j=0;j<m;j++)//把第i位密码匹配到的子串位置都枚举一遍
     //j表示第i位密码匹配到的位置,因为不能包含子串,所以不能匹配到m这个位置
      for(char k='a';k<='z';k++)//把第i+1所有可能的字母都枚举一遍
       {
           //匹配过程:寻找当第i+1的位置是k时,并且密码已经生成了第i位,匹配的子串的位置是j时,能跳到哪个位置
           int u=j;
           while(u&&str[u+1]!=k) u=ne[u];
           if(str[u+1]==k) u++;

           if(u<m) f[i+1][u]=(f[i+1][u]+f[i][j])%mod;
           //因为是从f[i][j](i+1的位置为k)跳到f[i+1][u]这个位置,所以f[i+1][u]=f[i+1][u]+f[i][j];
           /*
           注:可能存在重边,因为j不同但ne[j]是相同的,并且k是相同的,所以此时
           f[i][j1]和f[i][j2]跳到的位置是一样的(k相同,ne[j1]=ne[j2])
           */
       }

    int res=0;
    for(int i=0;i<m;i++) res=(res+f[n][i])%mod;
    //将所有的方案数加起来即为总方案数
    printf("%d",res);

    return 0;
}