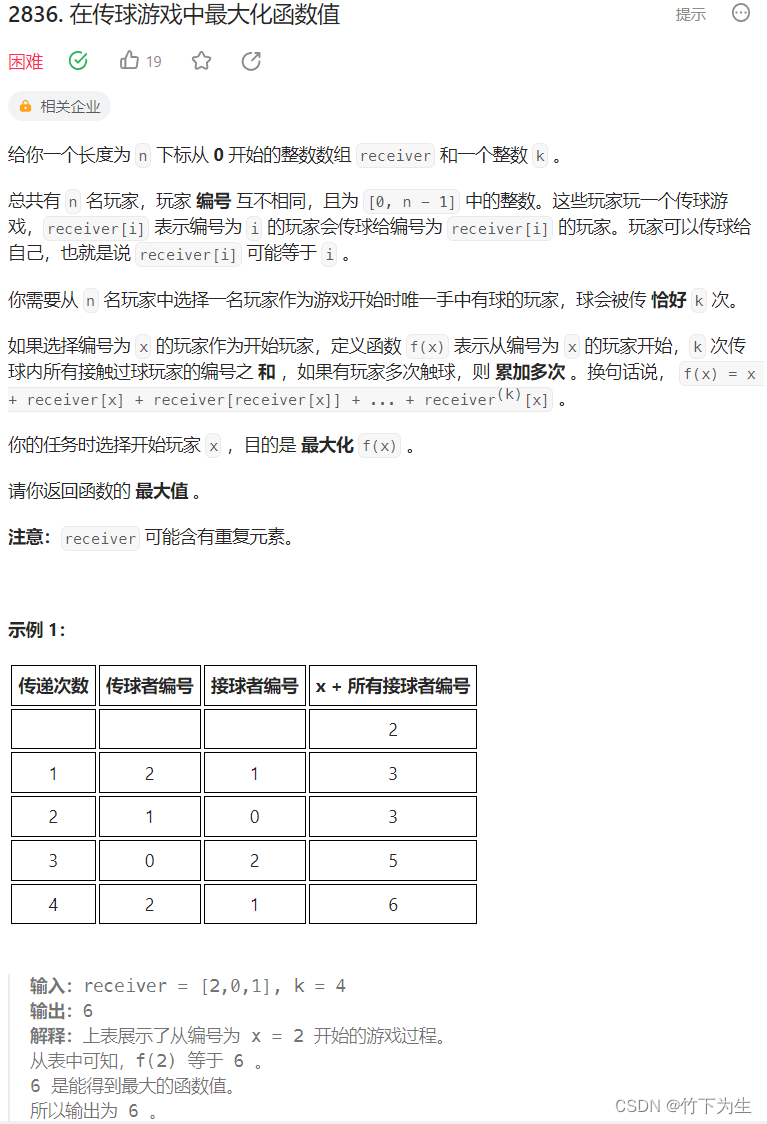
Python解决固定费用问题

具体文章参考博文

问题描述

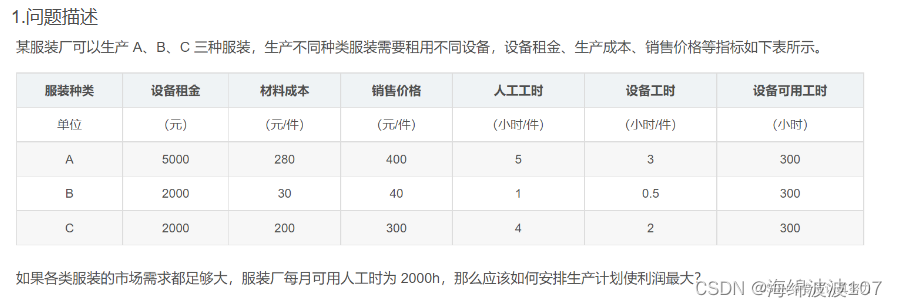
源代码

import pulp      # 导入 pulp 库

# 主程序
def main():
    # 固定费用问题(Fixed cost problem)
    print("固定费用问题(Fixed cost problem)")
    # 问题建模：
    """
        决策变量：
            y(i) = 0, 不生产第 i 种产品
            y(i) = 1, 生产第 i 种产品            
            x(i), 生产第 i 种产品的数量, i>=0 整数
            i=1,2,3
        目标函数：
            min profit = 120x1 + 10x2+ 100x3 - 5000y1 - 2000y2 - 2000y3
        约束条件：
            5x1 + x2 + 4x3 <= 2000
            3x1 <= 300y1
            0.5x2 <= 300y2
            2x3 <= 300y3
        变量取值范围：
            0<=x1<=100, 0<=x2<=600, 0<=x3<=150, 整数变量
            y1, y2 ,y3 为 0/1 变量 
    """
    # 1. 固定费用问题(Fixed cost problem), 使用 PuLP 工具包求解
    # (1) 建立优化问题 FixedCostP1: 求最大值(LpMaximize)
    FixedCostP1 = pulp.LpProblem("Fixed_cost_problem_1", sense=pulp.LpMaximize)  # 定义问题，求最大值
    # (2) 建立变量
    x1 = pulp.LpVariable('x1', cat='Binary')  # 定义 x1，0-1变量，是否生产 A 产品
    x2 = pulp.LpVariable('x2', cat='Binary')  # 定义 x2，0-1变量，是否生产 B 产品
    x3 = pulp.LpVariable('x3', cat='Binary')  # 定义 x3，0-1变量，是否生产 C 产品
    y1 = pulp.LpVariable('y1', lowBound=0, upBound=100, cat='Integer')  # 定义 y1，整型变量
    y2 = pulp.LpVariable('y2', lowBound=0, upBound=600, cat='Integer')  # 定义 y2，整型变量
    y3 = pulp.LpVariable('y3', lowBound=0, upBound=150, cat='Integer')  # 定义 y3，整型变量
    # (3) 设置目标函数
    FixedCostP1 += pulp.lpSum(-5000*x1-2000*x2-2000*x3+120*y1+10*y2+100*y3)  # 设置目标函数 f(x)
    # (4) 设置约束条件
    FixedCostP1 += (5*y1 + y2 + 4*y3 <= 2000)  # 不等式约束
    FixedCostP1 += (3*y1 - 300*x1 <= 0)  # 不等式约束
    FixedCostP1 += (0.5*y2 - 300*x2 <= 0)  # 不等式约束
    FixedCostP1 += (2*y3 - 300*x3 <= 0)  # 不等式约束
    # (5) 求解
    FixedCostP1.solve()
    # (6) 打印结果
    print(FixedCostP1.name)
    if pulp.LpStatus[FixedCostP1.status] == "Optimal":  # 获得最优解
        for v in FixedCostP1.variables():
            print(v.name, "=", v.varValue)  # 输出每个变量的最优值
        print("F(x) = ", pulp.value(FixedCostP1.objective))  # 输出最优解的目标函数值
    return

if __name__ == '__main__':
    main()

运行结果