链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
给定一个长度为 nnn 的数组 aaa,求数组所有非空子序列权值的最小值。
定义子序列 ai,aj,…,aka_i,a_{j},\dots,a_kai,aj,…,ak 的权值为
其中 &\&& 为二进制中的按位与
按位与的定义:按位与_百度百科
输入描述:
第一行包含一个正整数 nnn (1≤n≤20)(1 \le n \le 20)(1≤n≤20) 代表数组长度。
第二行包含 nnn 个正整数 aia_iai (1≤ai≤109)(1 \le a_i \le 10 ^ 9)(1≤ai≤109) 代表数组中每个数的值。
输出描述:
输出数组中所有非空子序列权值的最小值。
示例1
输入
6 1 1 4 5 1 4
输出
0
备注:
子序列不一定连续
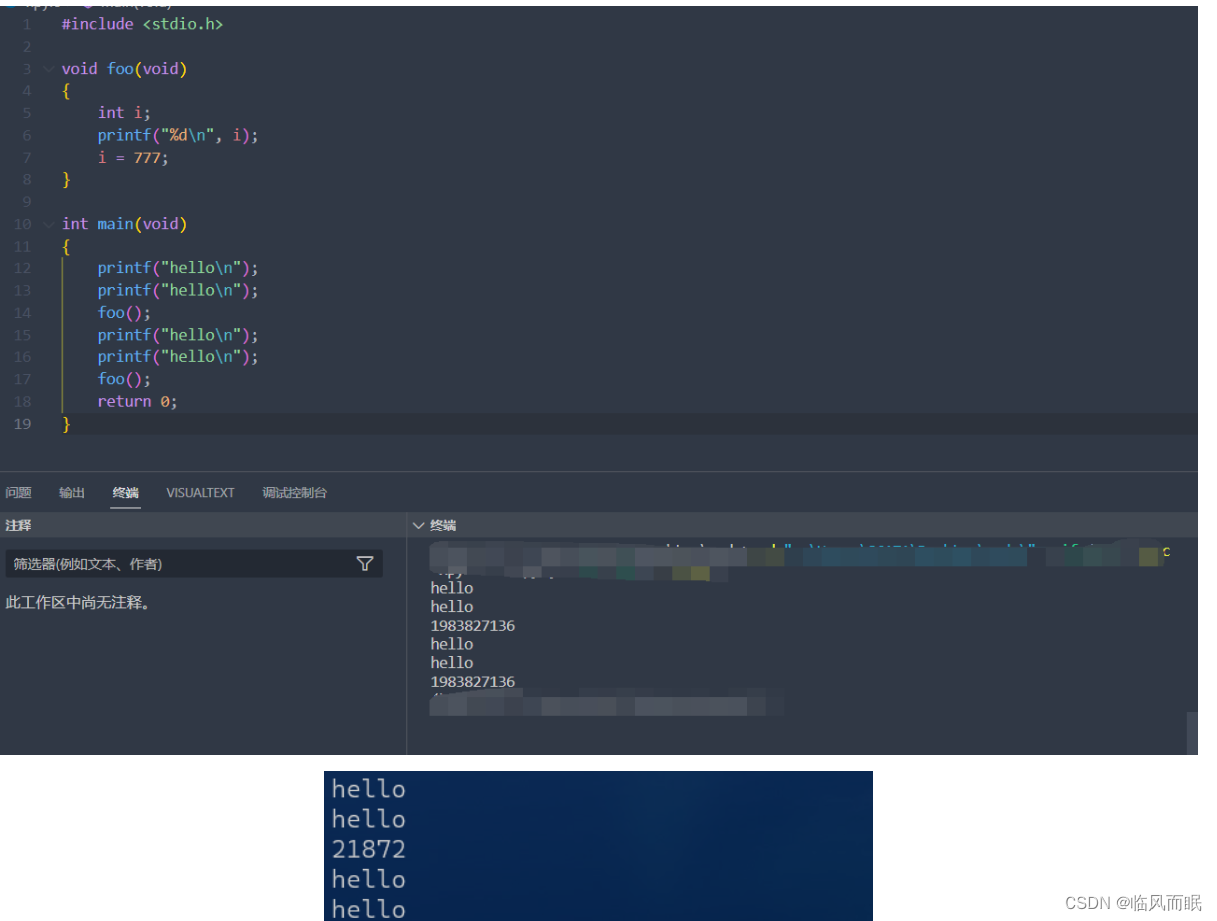
//首先了解位运算规则,这里官方也是很贴心,给了链接去查看“&”的用法

//这题本人就属于想复杂的那种,这题就是签到题,看提交量和通关率蛮高的(但是居然没人第二题的高,显然有很多同学也入坑了,没有正确理解题意),就我们学校来说,这道题通关的还是蛮多的,大一新生都会做,看来我这个大三学长要加油了。
//我当时看到子序列这个东西的时候,就想复杂了,觉得说,怎么才能实现这些子序列,下面是我的猜想,为了区别,我以1-6为例。
//如上图(可能本人存在写漏的情况),起初也想到了排序,因为相同的两个数的按位与运算结果还是这个数,但是如果这6个数不同呢,于是出现了上述例子,我当时在想如何实现这些子序列(题目最后也备注了子序列不一定连续,那正印证我的猜想),于是就在这些个子序列中迷失自我,想着怎么实现,然后最后要么通过数组存起来排序,输出第一个,要么就在线比较。
//下面阐述正确思想,本题就在于求子序列最小的按位与结果,那么先将数组排序,将最小的一个数赋予x,y,x在循环中去和数组中的元素进行运算,然后和y进行比较,小于则更新y的值,这里最关键的就是x的运算,他形成的子序列就是12,123,1234,12345,123456(按本人给的例子),那么和本人所给的子序列相差很大,其实本人理解的没错,只是想复杂了,因为要想得到子序列中最小的按位与结果,那么肯定和最小值相关联,所以将数组排序,依次累按位与计算,就拿本人给的例子,146的按位与结果肯定是大于123的,同样都是三个数的子序列,又比如1234的按位与小于1346,我进行计算时,一定取得是最小的几个数,所以才有了排序,后面就直接累按位与计算,使得我们取他的子序列的时候,取相同个数的数组合的序列一定是所有数中最小的
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,a[24],i,x,y;
cin>>n;
for(i=0;i<n;i++)cin>>a[i];
sort(a,a+n);
x=y=a[0];
for(i=0;i<n;i++){
x=x&a[i];
if(x<y)y=x;
}cout<<y;
return 0;
}