概念
当我们将多个元素分配到不同的集合中,这些集合有的是相关的,有的是不相关的。并查集就是用来查找两个元素是否在同一个集合中的
其主要实现方式是:将所有的元素以下标的形式存储在数组中。例如一共有十个人,那么就将这些人编号为0到9,然后用0到9的下标表示这些人,初始数组存储的全是-1
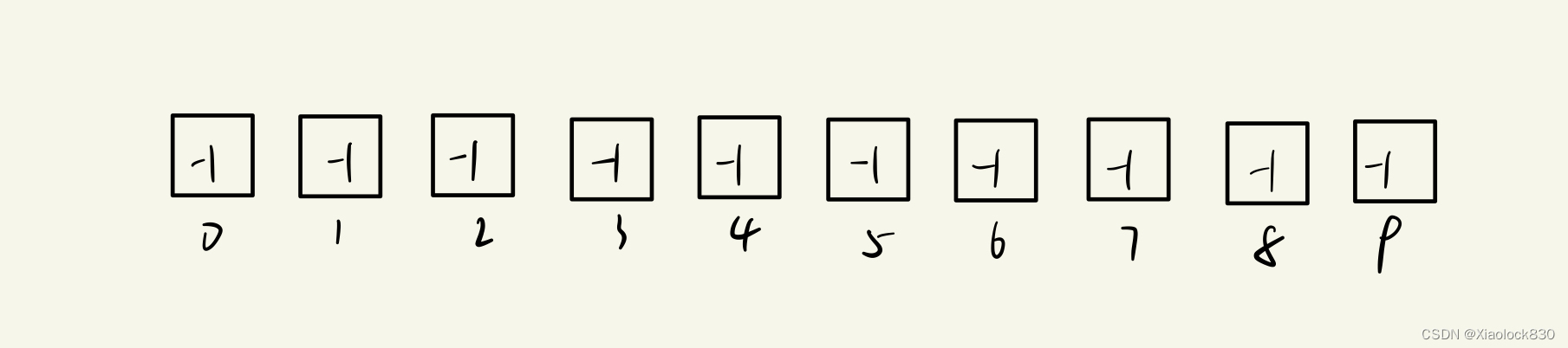
数组中存储的数据则代表他们之间的关联方式,例如0,6,7,8互相认识,那么他们就是一个集合,而0号是这个集合中的老大,那么0下标就存储这个团体的人的个数的相反数:-4,其他的几个成员6,7,8,则分别存储他们认识的0的下标:0
如果我们还有另两个集合,例如1,4,9是一个集合,1是老大,4和9存储1的下标,那么4和9存储1,1下标存储-3,而2,3,5是另一个集合,2是老大,则3,5存储2下标,2存储-3
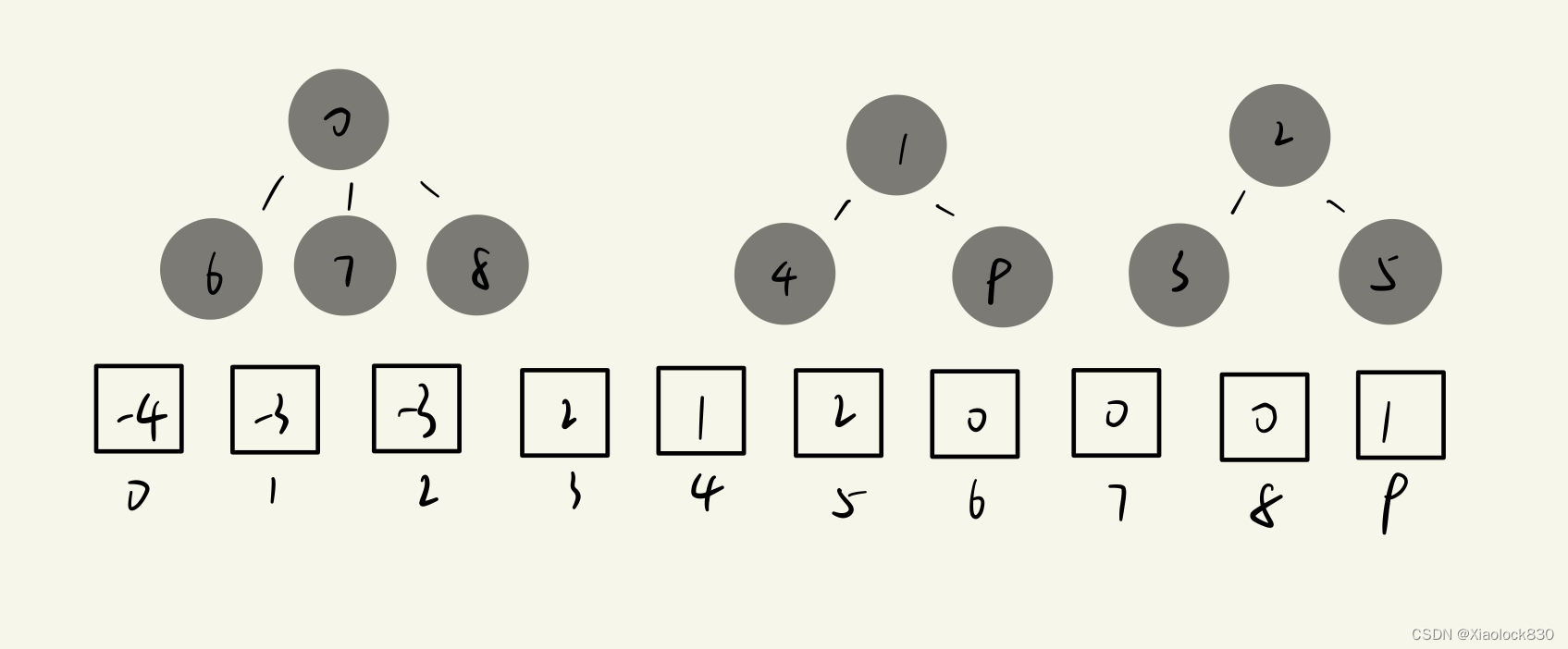
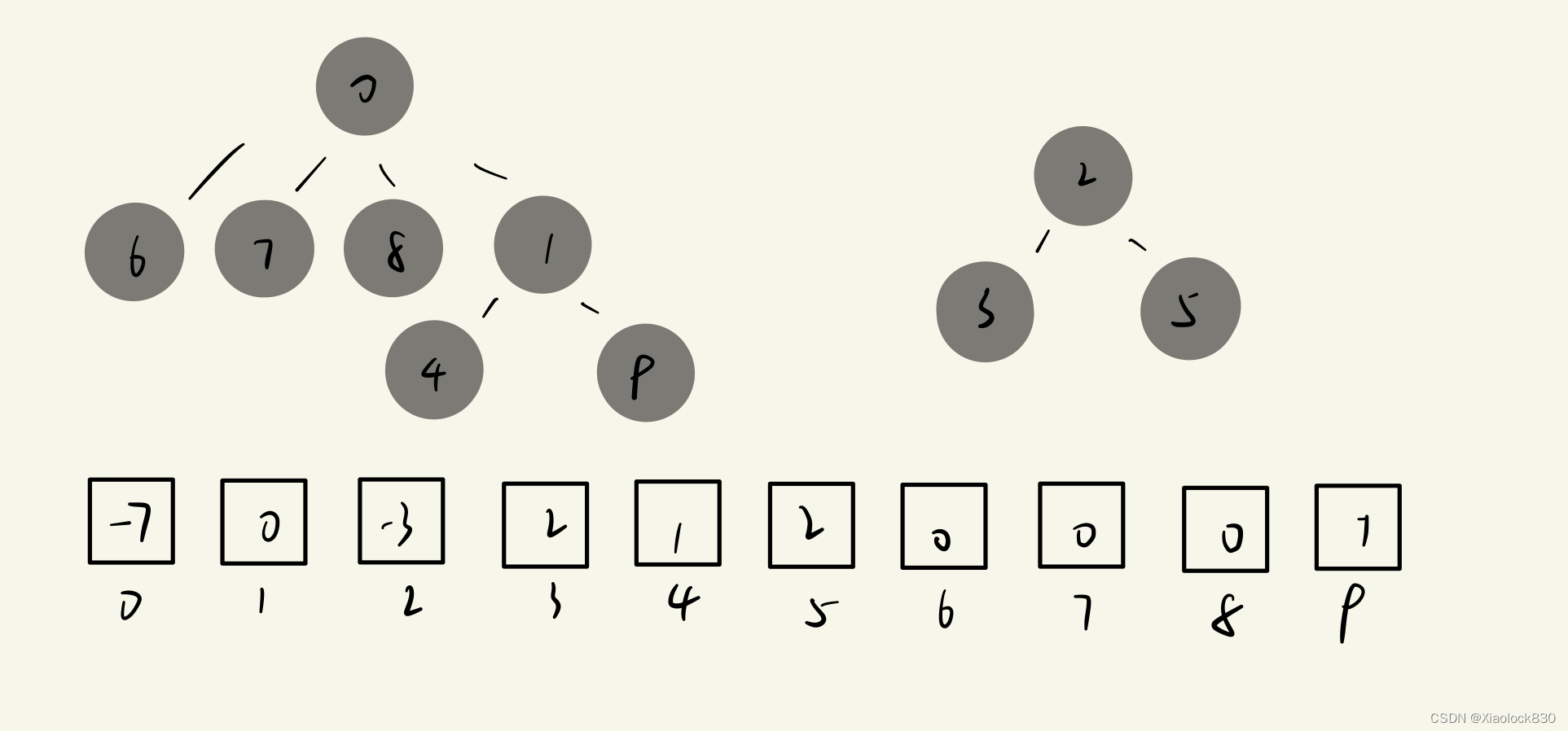
当我们的集合1和集合2的某一位互相认识了,那么根据朋友的传递原理,我们的集合1和集合2就都互相认识了,那么就会变成一个更大的集合,其中如果让0做老大,1隶属于0下标,那么就会形成下面的样子
0下标就存储了这个大集合的人数的相反数:-7,而1则从老大变成了平民,因此存储老大的下标:0,其他的都是不变的
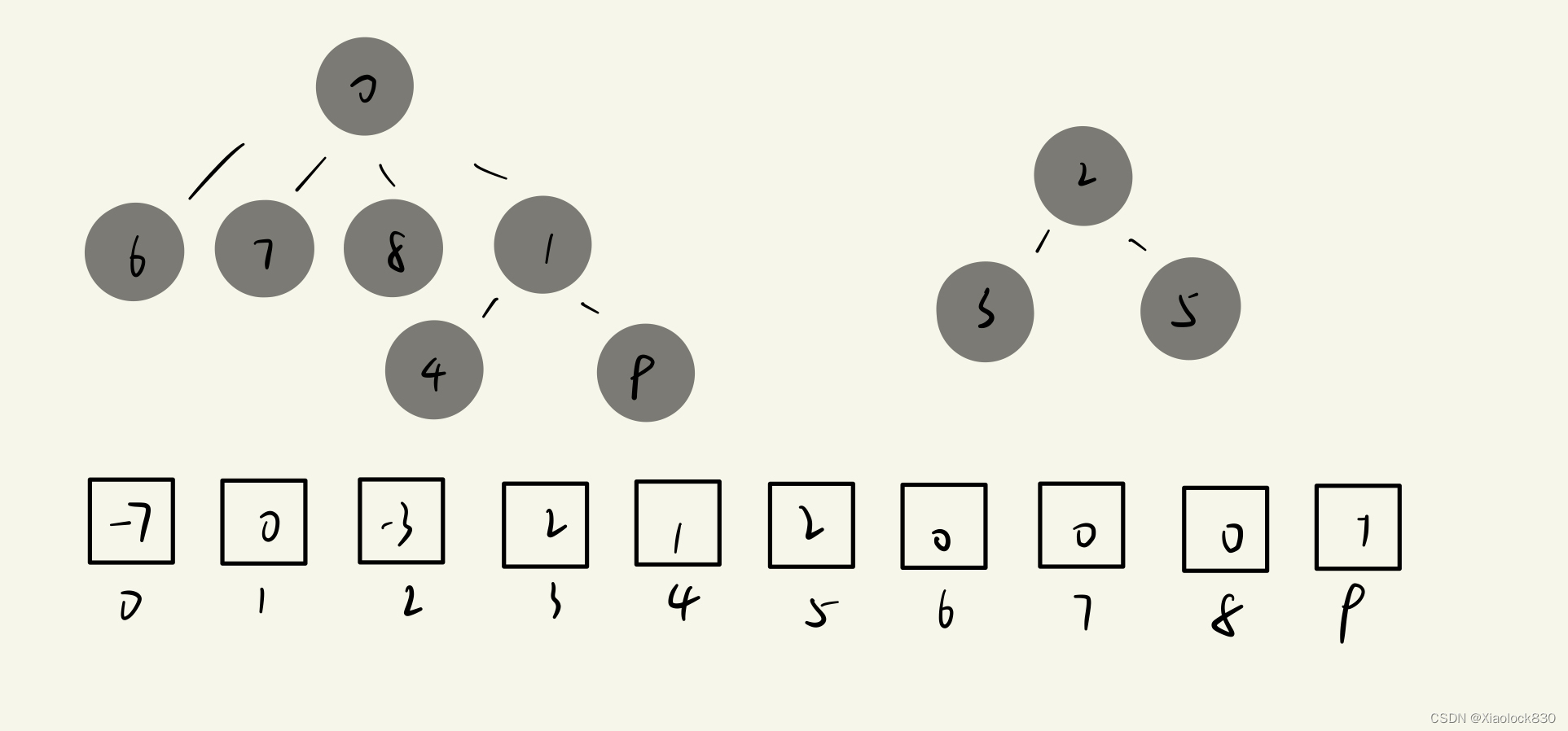
通过上面这个基本的原理,我们可以自己实现一个并查集
MyUnionFindSet
变量和构造方法
我们的底层数据结构是数组,在创建的时候,需要给数组传递一个创建的大小,并且用Arrays.fill方法,将数组的全部元素置为-1
public int[] elem;
public MyUnionFindSet(int n){
this.elem = new int[n];
Arrays.fill(elem, -1);//初始化数组全为-1
}
寻找根节点
这个方法就是用来找集合中的老大的
通过之前的概念的介绍,我们知道,只有老大存储的是负数,而其他下标则存储其父节点的下标。所以我们可以用一个循环,当这个下标对应的数据不是负数,那么就让x变为这个下标对应的数据,直到找到负数,就返回这个x
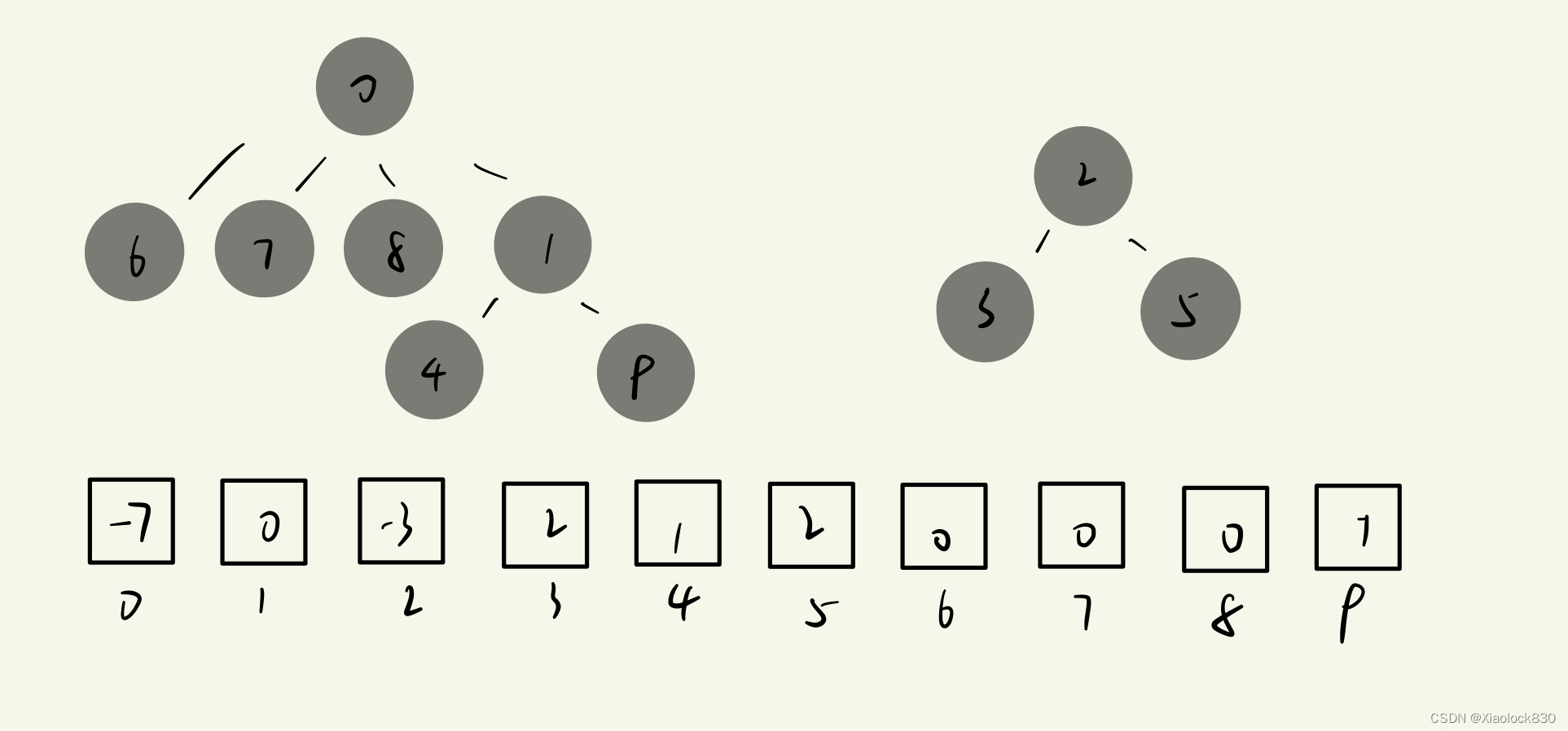
例如我们这个图中,如果我们传递的参数是9,那么elem[9]是1,那么x就变成1,elem[1]是0,那么x就变成0,elem[0]是-7,所以0是根节点,返回0
/**
* 查找x下标数据的根节点
* @param x
* @return 根节点的下标
*/
public int findRoot(int x){
if(x < 0){
throw new ArrayIndexOutOfBoundsException("下标不能是负数");
}
while(elem[x] >= 0){
x = elem[x];
}
return x;
}
判断两节点是否在同一个集合
当两个节点在同一个集合中,说明他们的根节点一定是相通的,所以我们可以调用findRoot方法,来找到两个节点的根节点,判断是否相同,相同返回true,不同返回false
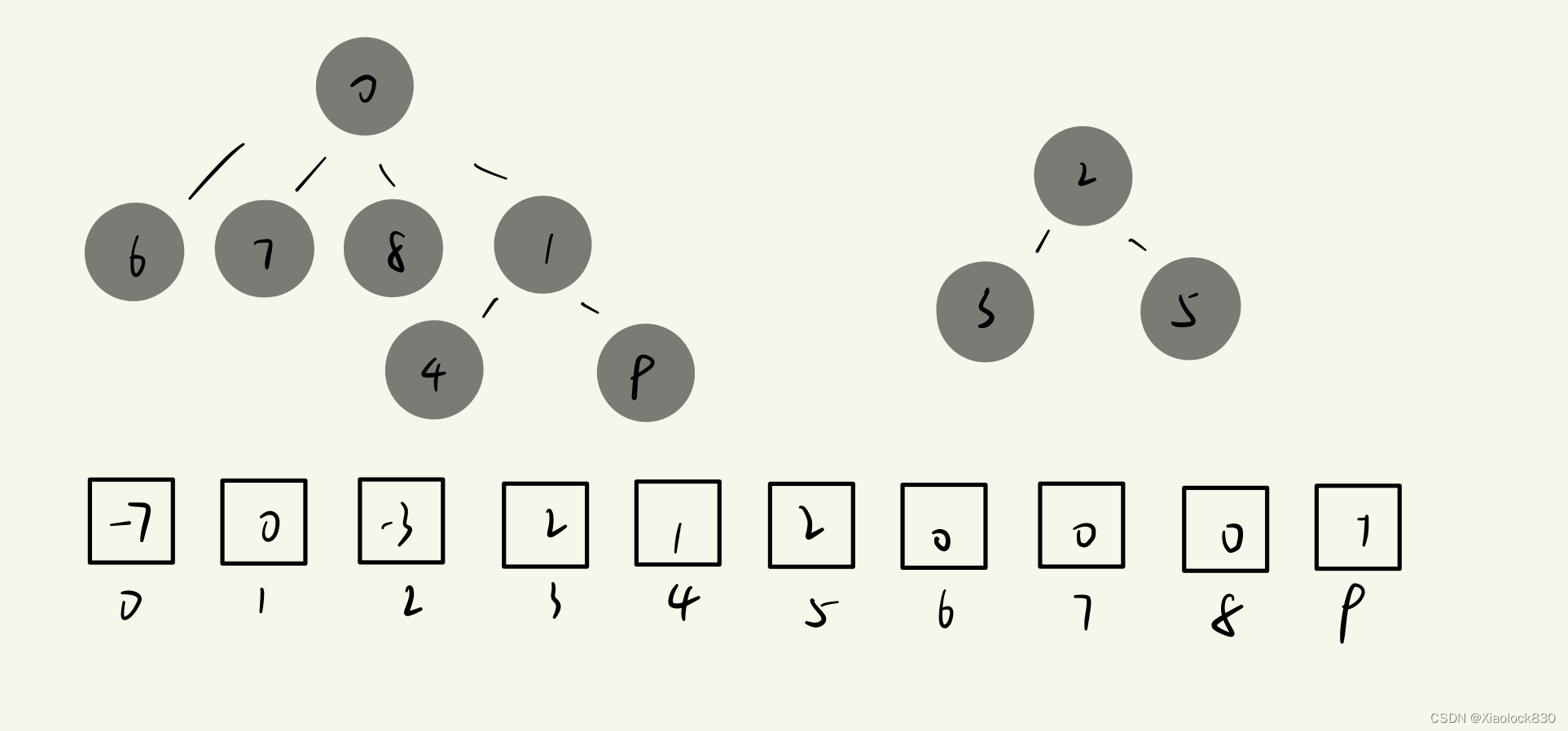
/**
* 查询x1和x2是否在同一个集合中
* @param x1
* @param x2
* @return
*/
public boolean isSameUnionFindSet(int x1, int x2){
int index1 = findRoot(x1);
int index2 = findRoot(x2);
if(index1 == index2){
return true;
}
return false;
}
合并两个集合
通过刚才的图片我们可以知道,当两个节点相连时,如果这两个节点不是根节点,那么就应该找到这两个节点的根节点,如果根节点相同,说明这两个节点已经在同一个集合中了,那么就不用合并了。
而如果根节点不相同,那么就和我们刚才讲的情形类似,就是把0和1相连,这时改变的只有0下标的值和1下标的值,其他的下标的值都是不变的
我们可以看到,0下标的值变成了两个集合的节点数目的总和的相反数,也就是0下标的值加上1下标的值:-7,而1下标的值则是直接改为了0
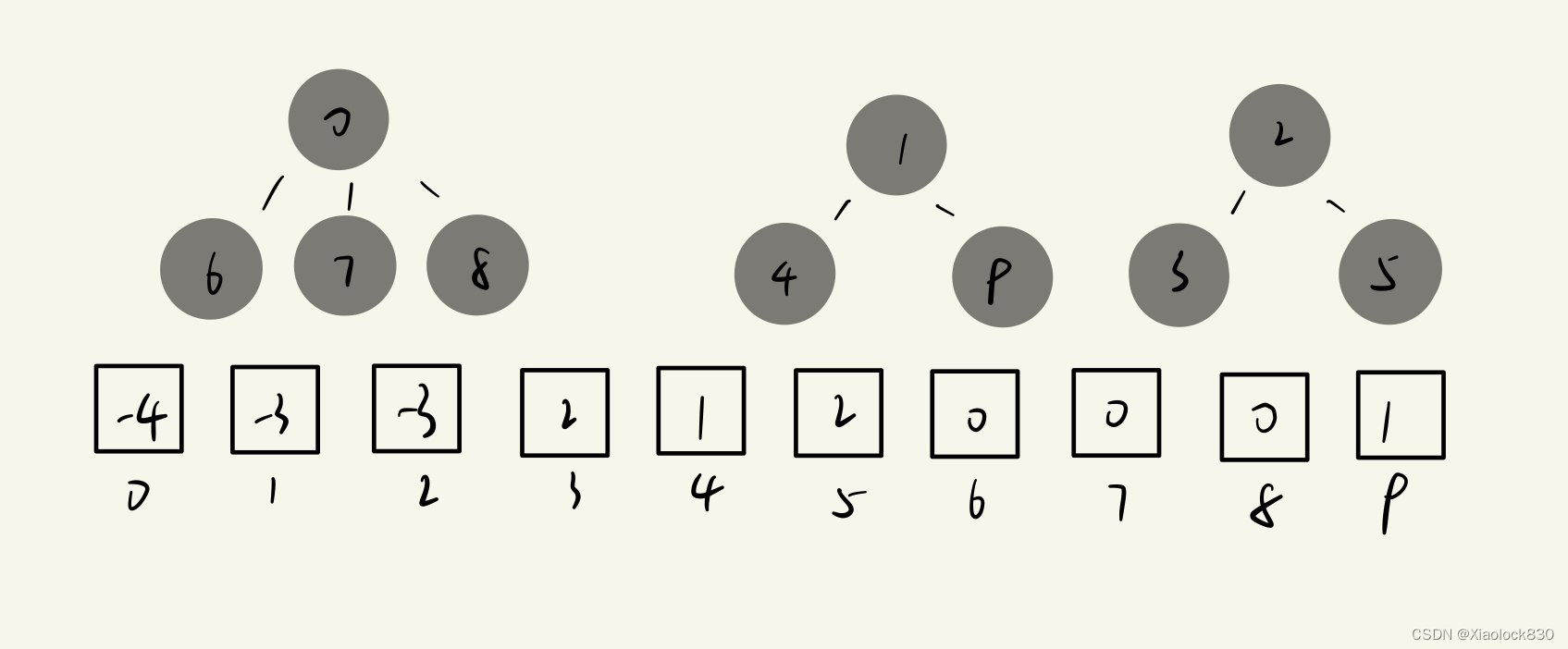
所以,我们就先找到x1,x2的根节点,判断是否相等,相等则直接返回。我们这里实现的逻辑x1是0,x2是1,所以
elem[0] = elem[0] + elem[1]
elem[1] = 0
也就是:
elem[index1] = elem[index1] + elem[index2]
elem[index2] = index1
完整代码如下:
/**
* 合并x1,x2所在的两个集合
* @param x1
* @param x2
*/
public void union(int x1, int x2){
int index1 = findRoot(x1);
int index2 = findRoot(x2);
if(index1 == index2){
System.out.println("x1和x2已经在同一个集合中了");
return;
}
elem[index1] = elem[index1] + elem[index2];
elem[index2] = index1;
}
获取集合的个数
可以看到,集合的个数等于所有老大的个数,等于数组中负数的个数
public int getCount(){
int count = 0;
for (int x:elem) {
if(x < 0){
count++;
}
}
return count;
}
打印
public void print(){
for (int x:elem) {
System.out.print(x + " ");
}
System.out.println();
}
测试
按照我们上面的图进行合并元素,最终可以得到结果是正确的
public static void main(String[] args) {
MyUnionFindSet myUnionFindSet = new MyUnionFindSet(10);
System.out.println("合并0和6");
myUnionFindSet.union(0,6);
System.out.println("合并0和7");
myUnionFindSet.union(0,7);
System.out.println("合并0和8");
myUnionFindSet.union(0,8);
System.out.println("合并1和4");
myUnionFindSet.union(1,4);
System.out.println("合并1和9");
myUnionFindSet.union(1,9);
System.out.println("合并2和3");
myUnionFindSet.union(2,3);
System.out.println("合并2和5");
myUnionFindSet.union(2,5);
myUnionFindSet.print();
System.out.println("合并8和1");
myUnionFindSet.union(8,1);
myUnionFindSet.print();
System.out.println("查找是否为同一个集合");
System.out.println(myUnionFindSet.isSameUnionFindSet(6,9));
System.out.println(myUnionFindSet.isSameUnionFindSet(8,2));
}