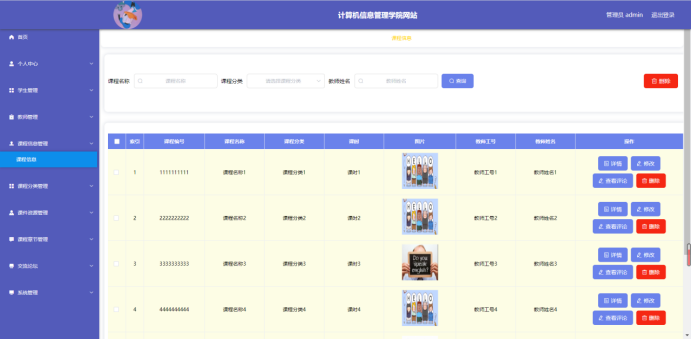
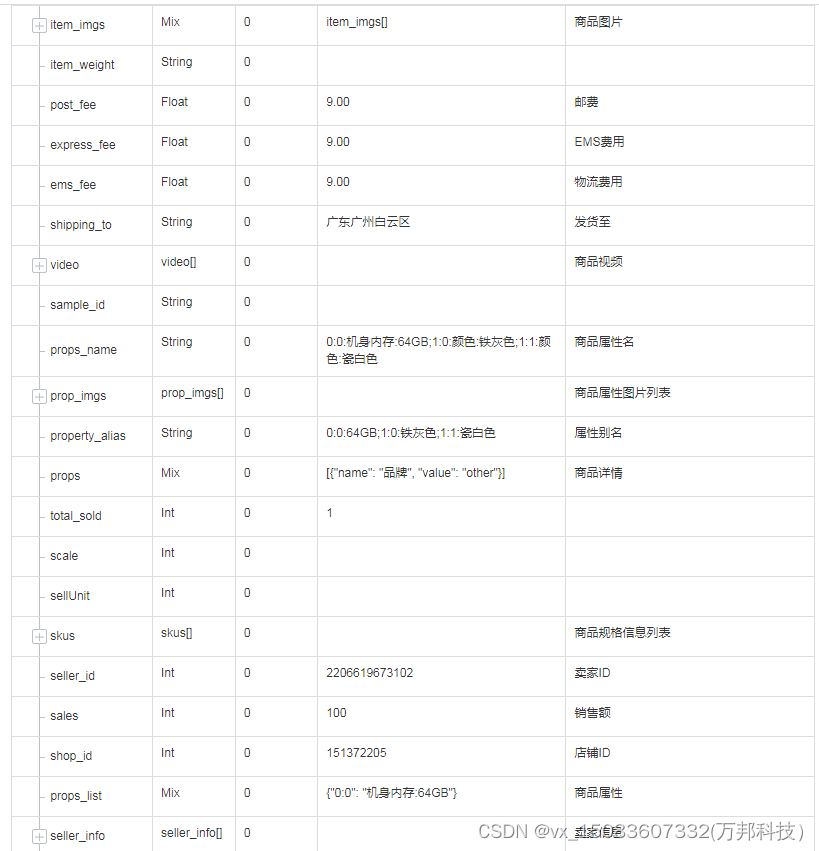
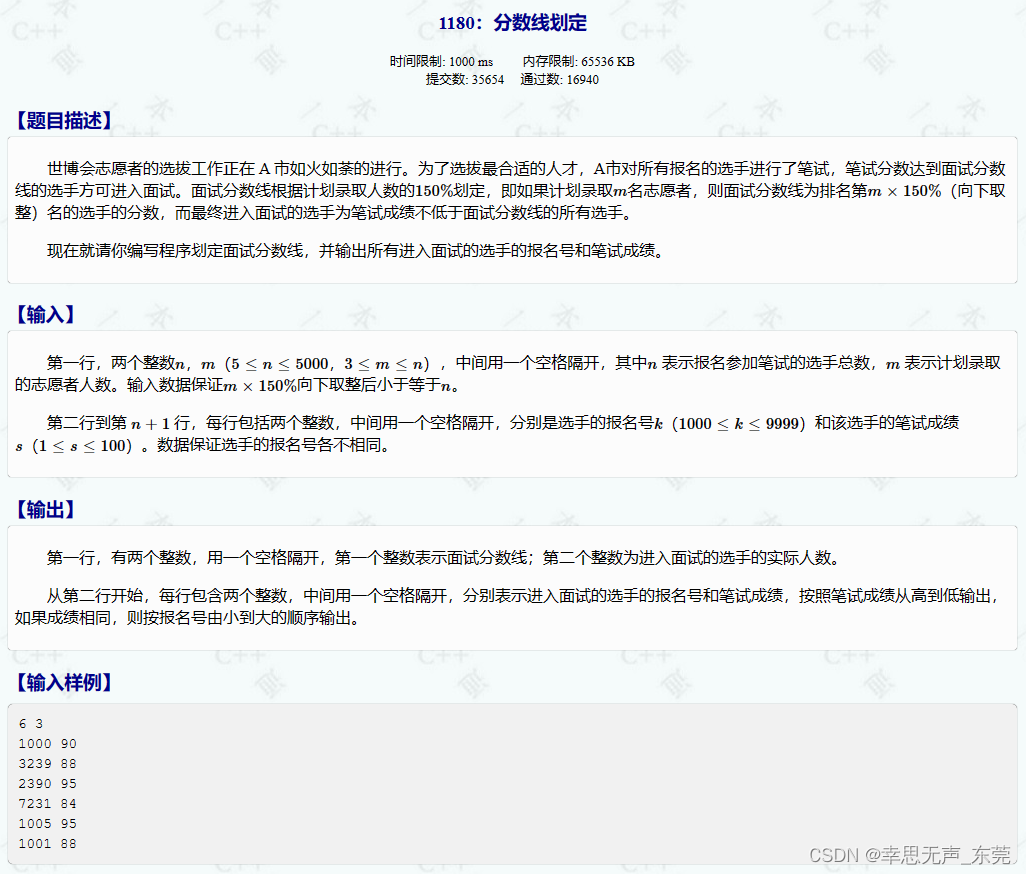
1. 子数组最大平均数 I

最大平均数
给你一个由 n 个元素组成的整数数组 nums 和一个整数 k 。
请你找出平均数最大且长度为 k 的连续子数组，并输出该最大平均数。
任何误差小于 10-5 的答案都将被视为正确答案。
示例 1：

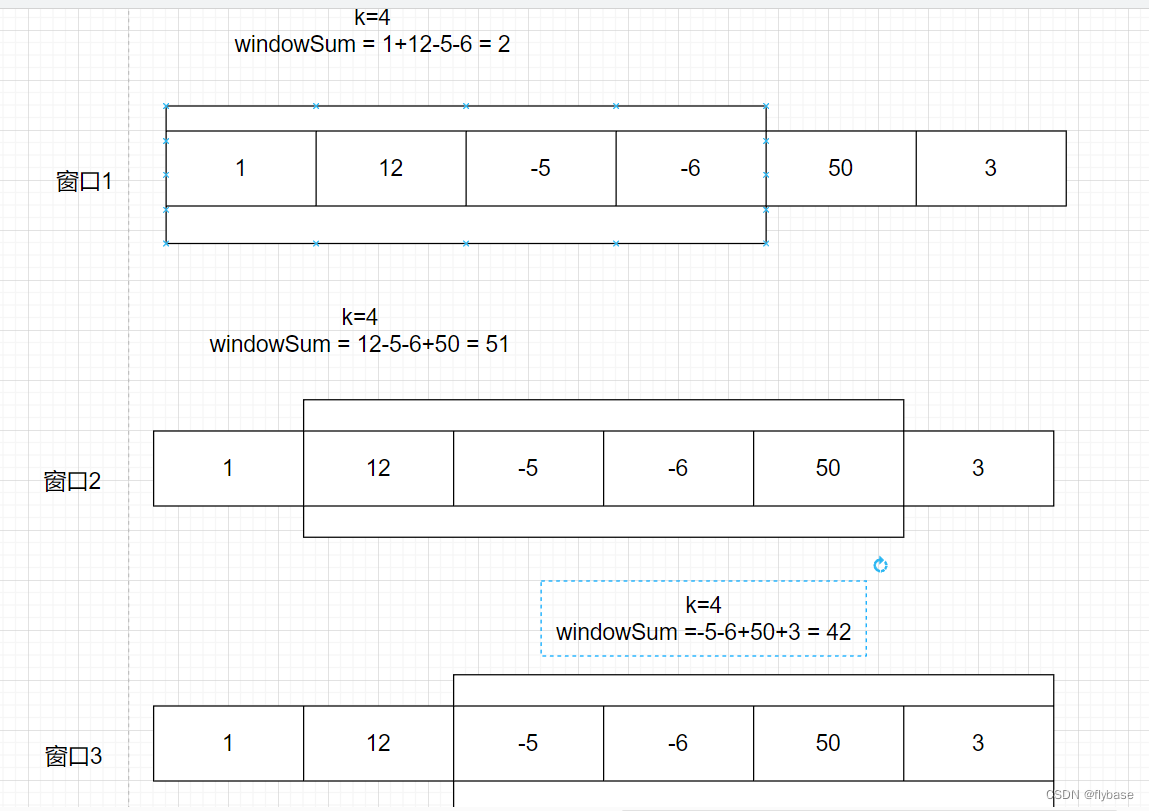
输入：nums = [1,12,-5,-6,50,3], k = 4
输出：12.75
解释：最大平均数 (12-5-6+50)/4 = 51/4 = 12.75
示例 2：

输入：nums = [5], k = 1
输出：5.00000

1.1 滑动窗口

本质就是计算每个窗口内的总和，然后将每个窗口的总和进行相比，找出最大的数，然后/k就是最大平均值。每次移动的时候都需要先将之前左窗口的元素先减去，然后再添加新进来的右元素，因为并不好直接计算 k的序列里面的元素和，所以需要先算出第一个窗口的和，然后再移动窗口。
在这里插入图片描述

   public double findMaxAverage(int[] nums, int k) {
        if(k>nums.length || nums.length<1 || k<1) return 0.0;
        
        int windowSum = 0;
        // 先计算第一个窗口总和
        for(int i=0;i<k;i++){
            windowSum +=nums[i];
        }
        
        int res = windowSum;
        // 移动窗口，减去左元素，添加新的右元素
        for(int right = k;right<nums.length;right++){
            windowSum  = windowSum +nums[right]-nums[right-k];
            res = Math.max(res,windowSum);
        }

        return (double)res/k;
    }

2. 最长连续递增序列

给定一个未经排序的整数数组，找到最长且连续递增的子序列，并返回该序列的长度。

连续递增的子序列可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列。

示例 1：

输入：nums = [1,3,5,4,7]
输出：3
解释：最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被 4 隔开。
示例 2：

输入：nums = [2,2,2,2,2]
输出：1
解释：最长连续递增序列是 [2], 长度为1。

2.1 遍历统计递增长度

遍历数组，统计每一个递增的长度，一旦出现了前一个元素比当前元素大或者等于的情况下，当前这个递增长度就设置成1，然后等待下一次递增，只需要将这些递增结果进行比较，就能获得最长的递增长度。

    public int findLengthOfLCIS(int[] nums) {
        // 当前最长的区间长度
        int curLen = 1;
        // 结果
        int res = 1;
        for(int i = 1;i<nums.length;i++){
            // 不符合递增
            if(nums[i-1] >= nums[i]){
                curLen = 1;
            }else{
                curLen++;
            }
            res = Math.max(res,curLen);
        }

        return res;
    }

2.2 滑动窗口

需要定义两个指针，left表示滑动窗口的起始位置，right表示滑动窗口的结束位置，遍历的时候一旦遇到不是递增的情况下，left=right, 否则就是right一直右移，然后将每一次遍历的长度进行比较，找出最长的一个。需要注意的是这个right需要大于0，否则会出现越界的情况。

   public int findLengthOfLCIS(int[] nums) {
        int left =0;
        int right = 0;
        int res = 0;
        while(right < nums.length){
            if(right >0 &&nums[right-1] >= nums[right]){
                left = right;
            }
            right++;
            res = Math.max(res,right-left);
        }
        return res;
    }