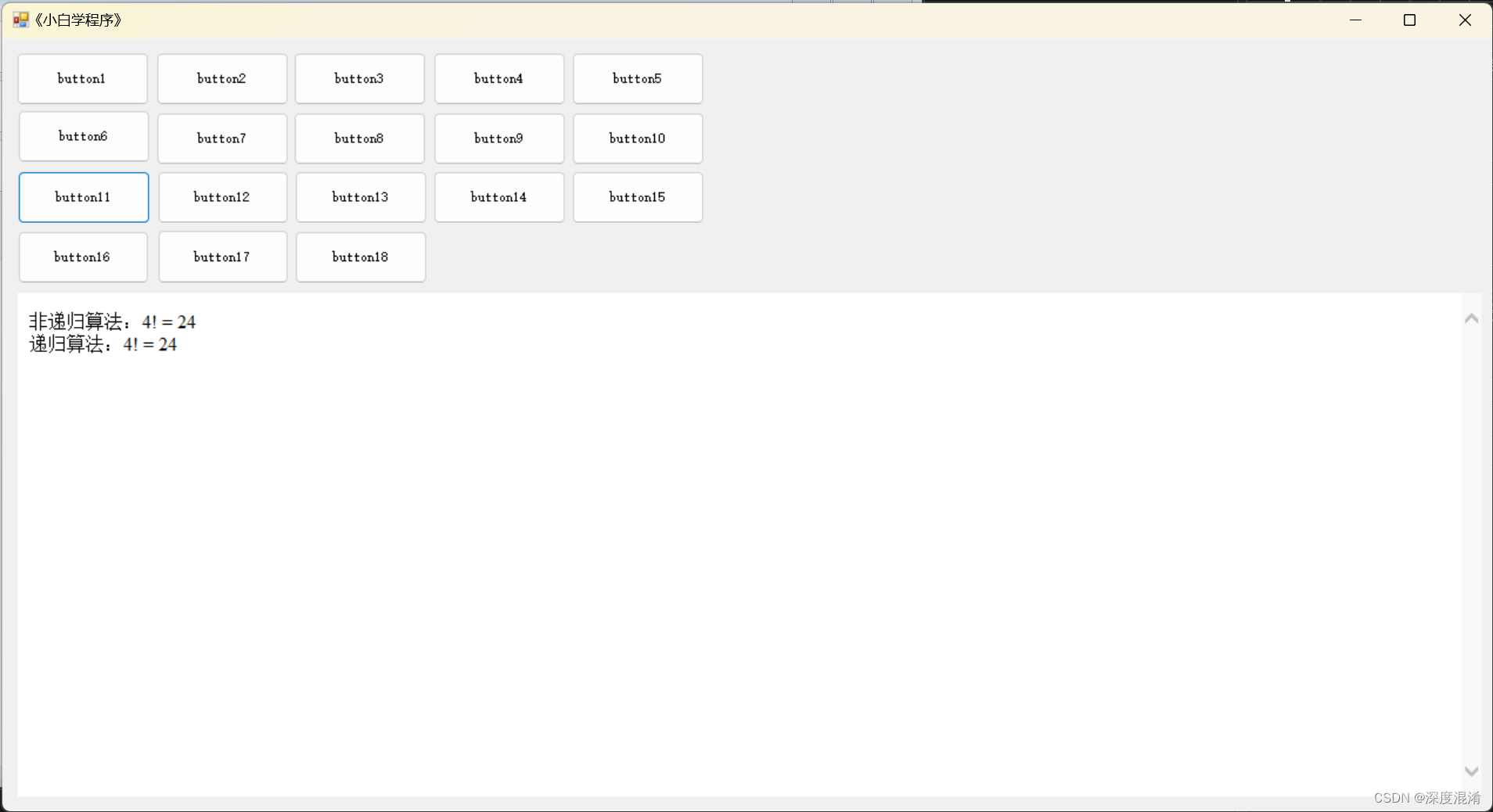
1 文本格式

/// <summary>
/// 阶乘的非递归算法
/// </summary>
/// <param name="a"></param>
/// <returns></returns>
private int Factorial_Original(int a)
{
    int r = 1;
    for (int i = a; i > 1; i--)
    {
        r = r * i;
    }
    return r;
}

/// <summary>
/// 阶乘的递归算法
/// 递归简单理解就是函数调用自己（当然参数不同哈！）
/// </summary>
/// <param name="a"></param>
/// <returns></returns>
private int Factorial(int a)
{
    if (a > 1) return a * Factorial(a - 1);
    else return 1;
}

/// <summary>
/// 《小白学程序》第十一课：阶乘（Factorial）的计算方法与代码
/// 阶乘是基斯顿·卡曼（Christian Kramp，1760～1826）于 1808 年发明的运算符号，是数学术语。
/// 一个正整数的阶乘（factorial）是所有小于及等于该数的正整数的积，并且0的阶乘为1。自然数n的阶乘写作n!。
/// 1808年，基斯顿·卡曼引进这个表示法。亦即 n! = 1×2×3×...×(n-1)×n。
/// 阶乘亦可以递归方式定义：
/// 0! = 1
/// n! = (n-1)! × n
/// 
/// 本节课接触了函数(阶乘函数)。
/// </summary>
/// <param name="sender"></param>
/// <param name="e"></param>
private void button11_Click(object sender, EventArgs e)
{
    int n = 4;

    StringBuilder sb = new StringBuilder();
    sb.AppendLine("非递归算法：" + n + "! = " + Factorial_Original(n) + "<br>");
    sb.AppendLine("递归算法：" + n + "! = " + Factorial(n) + "<br>");
    webBrowser1.DocumentText = sb.ToString();
}
 

2 代码格式

/// <summary>
/// 阶乘的非递归算法
/// </summary>
/// <param name="a"></param>
/// <returns></returns>
private int Factorial_Original(int a)
{
    int r = 1;
    for (int i = a; i > 1; i--)
    {
        r = r * i;
    }
    return r;
}

/// <summary>
/// 阶乘的递归算法
/// 递归简单理解就是函数调用自己（当然参数不同哈！）
/// </summary>
/// <param name="a"></param>
/// <returns></returns>
private int Factorial(int a)
{
    if (a > 1) return a * Factorial(a - 1);
    else return 1;
}

/// <summary>
/// 《小白学程序》第十一课：阶乘（Factorial）的计算方法与代码
/// 阶乘是基斯顿·卡曼（Christian Kramp，1760～1826）于 1808 年发明的运算符号，是数学术语。
/// 一个正整数的阶乘（factorial）是所有小于及等于该数的正整数的积，并且0的阶乘为1。自然数n的阶乘写作n!。
/// 1808年，基斯顿·卡曼引进这个表示法。亦即 n! = 1×2×3×...×(n-1)×n。
/// 阶乘亦可以递归方式定义：
/// 0! = 1
/// n! = (n-1)! × n
/// 
/// 本节课接触了函数(阶乘函数)。
/// </summary>
/// <param name="sender"></param>
/// <param name="e"></param>
private void button11_Click(object sender, EventArgs e)
{
    int n = 4;

    StringBuilder sb = new StringBuilder();
    sb.AppendLine("非递归算法：" + n + "! = " + Factorial_Original(n) + "<br>");
    sb.AppendLine("递归算法：" + n + "! = " + Factorial(n) + "<br>");
    webBrowser1.DocumentText = sb.ToString();
}