Problem - I - Codeforces
题意:

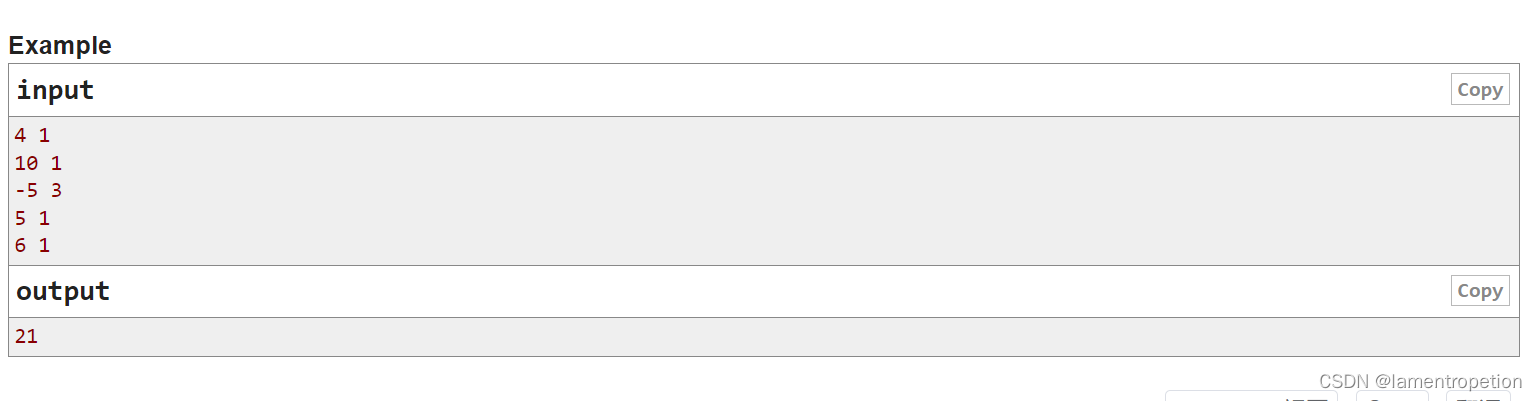
思路:
考虑暴力DP即可
设 dp[i][j][k]表示 前 i 个物品,已经翻倍了 j 次,A点数 - B点数为 k 的最大价值和
然后分为这6种决策分类讨论就好了

注意数组里不能有负数,要加个偏移量 P
Code:
#include <bits/stdc++.h>
#define int long long
using i64 = long long;
constexpr int N = 1e2 + 10;
constexpr int M = 1e5 + 10;
constexpr int P = 2600;
constexpr i64 Inf = 1e18;
constexpr int mod = 1e9 + 7;
constexpr double eps = 1e-6;
int n, K;
int v[N], t[N];
int dp[N][N][5220];
void solve() {
std::cin >> n >> K;
for (int i = 1; i <= n; i ++) {
std::cin >> v[i] >> t[i];
}
for (int i = 0; i <= n; i ++) {
for (int j = 0; j <= K; j ++) {
for (int k = -2600; k <= 2600; k ++) {
int tk = k + P;
dp[i][j][tk] = -Inf;
}
}
}
dp[0][0][0 + P] = 0;
for (int i = 1; i <= n; i ++) {
for (int j = 0; j <= K; j ++) {
for (int k = -2600; k <= 2600; k ++) {
int tk = k + P;
if (j >= 1) dp[i][j][tk] = std::max(dp[i][j][tk], dp[i - 1][j - 1][tk]);
if (k - t[i] * 2 >= -2600 && j >= 1) dp[i][j][tk] = std::max(dp[i][j][tk], dp[i - 1][j - 1][tk - t[i] * 2] + v[i]);
if (k + t[i] * 2 <= 2600 && j >= 1) dp[i][j][tk] = std::max(dp[i][j][tk], dp[i - 1][j - 1][tk + t[i] * 2] + v[i]);
dp[i][j][tk] = std::max(dp[i][j][tk], dp[i - 1][j][tk]);
if (k - t[i] >= -2600) dp[i][j][tk] = std::max(dp[i][j][tk], dp[i - 1][j][tk - t[i]] + v[i]);
if (k + t[i] <= 2600) dp[i][j][tk] = std::max(dp[i][j][tk], dp[i - 1][j][tk + t[i]] + v[i]);
}
}
}
int ans = -Inf;
for (int j = 0; j <= K; j ++) {
ans = std::max(ans, dp[n][j][0 + P]);
}
std::cout << ans << "\n";
}
signed main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t = 1;
while (t--) {
solve();
}
return 0;
}![[PyTorch][chapter 54][Variational Auto-Encoder 实战]](https://img-blog.csdnimg.cn/c27f973ceff14d1e95b4aac79292b719.png)