概念:
死码消除(dead code elimination, DCE) 是一种编译器优化技术, 作用是在编译阶段去掉对程序运行结果没有任何影响的代码
和 逃逸分析[1],内联优化[2]并称为 Go编译器执行的三个重要优化
效果:
对于 const.go代码如下:
package main
import "fmt"
func max(a, b int) int {
if a > b {
return a
}
return b
}
const a, b = 10, 20
func main() {
if max(a, b) == a {
fmt.Println(a)
}
}
对于var.go代码如下:
package main
import "fmt"
func max2(x, y int) int {
if x > y {
return x
}
return y
}
var x, y = 10, 20
func main() {
if max2(x, y) == x {
fmt.Println(x)
}
}
两个文件的差异,只在于 两个参数 是变量还是常量
分别编译 const.go 和 var.go, 生成的二进制文件大小如下:
go build -o 想要生成的二进制名称 想要编译的.go文件
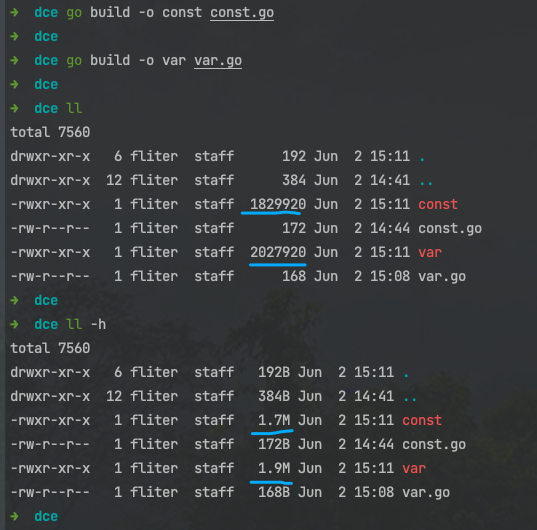
不难发现, const 比 var 体积小了约 10%
为何如此?
首先编译器会对max函数进行内联优化, const.go 优化后如下:
package main
import "fmt"
const a, b = 10, 20
func main() {
var result int
if a > b {
result = a
} else {
result = b
}
if result == a {
fmt.Println(a)
}
}
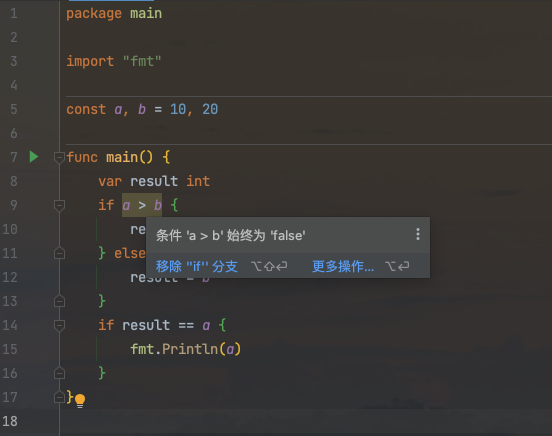
因为 a和b是常量, 永远有a<b, 编译器可以在编译时证明该分支永远不会为true, 因此编译器可以进一步优化代码为:
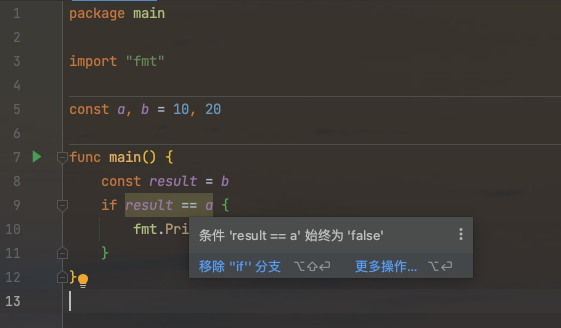
if a > b {}这个分支被消除了,这称为分支消除
又知道结果总是等于b,因此编译器还将进一步将代码优化为:
package main
const a, b = 10, 20
func main() {
const result = b
}
最后就是:
package main
func main() {
}
而对于var.go, 参数为 全局变量 不为常量,编译器并不知道运行过程中x、y会不会发生改变, 因此不能进行死代码消除.
这部分代码被编译到最终的二进制程序中, 造成 二进制文件 var 比 const 体积大了约 10%
分支消除是死码消除一种. 使用静态证明来表明一段代码永远不可达,通常会被称为死代码,它不需要在最终的二进制文件中编译和优化.
编译器在编译阶段, 死码消除与内联优化一起工作, 可以减少循环和分支产生的代码数量
参考资料
逃逸分析: https://dashen.tech/2021/05/29/golang%E9%80%83%E9%80%B8%E6%8A%80%E6%9C%AF%E5%88%86%E6%9E%90/
[2]内联优化: https://dashen.tech/2021/05/22/Go%E4%B8%AD%E7%9A%84%E5%86%85%E8%81%94%E4%BC%98%E5%8C%96
本文由 mdnice 多平台发布