-----------------------文末附往期文章链接--------------------

  关于分析反馈反馈系统的基本方法：可以看我之前的文章
             【模拟集成电路】反馈系统——基础到进阶（一）
             【模拟集成电路】反馈系统——基础到进阶（二）
  本文将对四种规范的反馈结构：电压-电压型（V-V）、电压-电流型(V-I)、电流-电流型(I-I)和电流-电压型(I-V)，通过二端口网络方法，考虑加载效应对闭环反馈的影响，并对相关参数进行说明。
反馈分析的困难

1.概述

  在求解反馈系统时，常规方法遵循以下步骤
  ①在合适的位置断开反馈环路，求出开环增益、输入和输出阻抗；
  ②根据开环增益确定“环路增益”，从其开环电路中确定各个闭环参数；
  ③用闭环增益对闭环系统进行分析；

  事实上上述步骤只能“不精确”的解决“小部分”问题，而实际电路往往是复杂的，如果想精确的对电路进行分析求解，那么需要了解反馈分析的五个“困难”。
  （1）由于“加载”效应，反馈环路会对前馈电路部分产生影响，只有默认反馈环路对前馈电路部分不产生影响时，才能直接将环路开环，因此直接断开环路是“不精确”的；
  （2）大多数反馈系统，无法明确的分解成“前馈网络”和“反馈网络”；
  （3）大多数反馈系统，不易被映射到规范的反馈结构（电压-反馈？/电压-电流反馈？）；
  （4）对反馈系统的分析，默认反馈环路中信号是沿着“正确的”单向流动的，而实际的信号流动方向是复杂的。
  （5）大多数电路系统，包含多个环路，难以分析。

上述反馈分析的困难，汇总与下表。

  对于上述反馈分析的困难，可以采用二端口方法、波特方法和麦德布鲁克方法进行更加精确的求解，如表2所示。具体细节后续展开。

2.二端口网络方法

  二端口网络方法，在考虑加载效应时，将环路进行开环，计算求得开环和闭环的环路增益，为简化计算，规定信号是单向流动的，即忽略前馈网络的反馈和反馈网络的前馈，该方法仅适用于规范的结构。

2.1二端口网络模型

  若将信号流动简化为单向流动，则二端口网络可简化为图2.1。

  但是实际信号流动是双向的，简化二端口模型通常不能满足要求，因此通过二端口网络方法对反馈系统分析，需要更加精确的二端口网络模型，精确的二端口网络模型如图2.2所示。其中图2.1（a）为“Z模型”由串联的输入和输出阻抗和电流控制电压源组成；图2.1（b）为“Y模型”由并联的输入和输出导纳和电压控制电流源组成；图2.1（c）和（d）为“混合模型”由阻抗、导纳、电压源和电流源组成。

  上述四种模型分别可以由两个方程描述

  其中应该注意，（1）$Y_{11}$与$Z_{11}$的倒数可能不相等，因为二者是在不同条件下得到的：前者是在输出短路时得到的，而后者是在输出开路时得到的；（2）以Z模型为例，Z11不一定等于Zin，因为输入阻抗是输出保持开路时求得；（2）$Z_{22}$不一定等于$Z_{out}$，前者是由输入开路计算，Zout是输入短路时计算；（4）在精确模型中，考虑了信号的反馈（输入回路中输出回路控制）。

2.2电压-电压反馈的加载

  如本节开始所讲，在运用如图2.2所示的模型时，默认信号单向流动，忽略前馈网络的反馈和反馈网络的前馈。
  对于电压-电压反馈，前馈网络的输出为受控电压源，输入控制量也为电压信号，因此适用于G模型，同理对于反馈网络，反馈网络的输出为受控电压源，输入控制量为电压信号，也同样适用于G模型。电压-电压反馈的电路模型如图2.3所示。

  对二端口网络进行分析，由KCL和KVL有

  求解得到

  整理成闭环增益形式 $A_{\nu ,open}/(1+\beta A_{\nu ,open})$，将式（2.6）分子分母除以$(1+g_{22}/Z_{in})(1+g_{11}{Z}_{out})$ 得到

  对比闭环增益形式，得到开环电压增益 $A_{\nu ,open}$ 反馈系数 $\beta$

  对开环增益进行分析，得到开环增益可以拆解成式（2.9）的形式

  其中第一项 $1+g_{22}/Z_{in}=(Z_{in}+g_{22})/Z_{in}$，其倒数 $Z_{in}/(Z_{in}+g_{22})$为阻抗分压形式；第三项 $1+g_{11}{Z}_{out}=(g_{11}^{-1}+Z_{out})/g_{11}^{-1}$，它的倒数 $g_{11}^{-1}/(g_{11}^{-1}+Z_{out})$ 代表另一个分压器，因此开环电路可以等效成图2.4的形式

  根据Z模型的数学表达式（2.4），可以对 $g_{11}$ 和 $g_{22}$ 进行求解

  根据数学公式可知， $g_{11}$ 可以通过使反馈网络输出开路（I2=0）得到， $g_{22}$ 可以通过使反馈网络输入短路（V1=0）得到，如图2.4（b）。由图2.3，对反馈系数进行求解，反馈网路为G模型，因此反馈系数

  注意，方向问题，在G模型中，I2的正方向是从V2灌进去的，因此实际电路中，该方向应该小心，如图2.5所示。

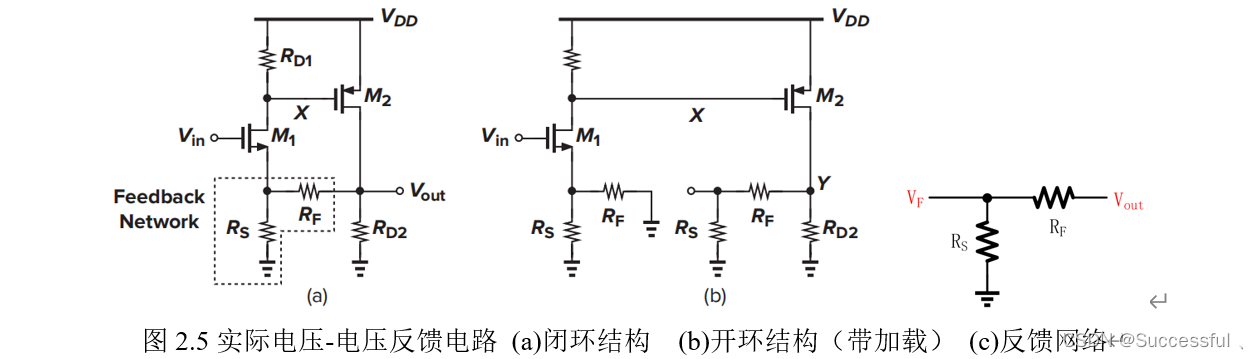
2.2电流-电压反馈的加载

  默认信号单向流动，忽略前馈网络的反馈和反馈网络的前馈。
  对于电流-电压反馈，前馈网络的输出为受控电流源，输入控制量为电压信号，因此适用于Y模型；对于反馈网络，反馈网络的输出为受控电压源，输入控制量为电流信号，适用于Z模型。电流-电压反馈的电路模型如图2.3所示。


  其 $Y_{21}$为前馈网络的跨导增益Gm，参考分析式（2.9），同理 ${\left(1+z_{22}{Y}_{11}\right)}^{-1}$ 和 ${\left(1+z_{11}{Y}_{22}\right)}^{-1}$ 分别对应开环结构输入端和输出端的两个分压器和分流器，则带有加载效应的开环放大器如图2.7所示。

  根据式(2.1)，通过对Z模型数学求解，可以得到 $z_{11}$ 和 $z_{22}$

  注意，方向问题，在Z模型中，I1的正方向是从V1灌进去的，实际电路如图2.8所示。

2.3电压-电流反馈的加载

  默认信号单向流动，忽略前馈网络的反馈和反馈网络的前馈。
  对于电压-电流反馈，前馈网络的输出为受控电压源，输入控制量为电流信号，因此适用于Z模型；对于反馈网络，反馈网络的输出为受控电流源，输入控制量为电压信号，适用于Y模型。电压-电流反馈的电路模型如图2.10所示。


  其 $Z_{21}$为前馈网络的跨阻增益Rm，参考分析式（2.9），同理 ${\left(1+y_{22}{Z}_{11}\right)}^{-1}$ 和 ${\left(1+y_{11}{Z}_{22}\right)}^{-1}$分别对应开环结构输入端的分流器和输出端的分压器，则带有加载效应的开环放大器如图2.11所示。

  根据式(2.2)，通过对Y模型数学求解，可以得到 $y_{11}$ 和 $y_{22}$

  根据数学公式可知， $y_{11}$ 可以通过使反馈网络输出短路（V2=0） 得到， $y_{22}$ 可以通过使反馈网络输入短路（V1=0） 得到，如图2.11所示开环原理图。对反馈系数进行求解，反馈网路为Y模型，因此反馈系数根据式（2.2）

  注意，方向问题，在Y模型中，I2的正方向是从V2灌进去的，实际电路如图2.8所示。

  根据图2.12(b)，可以有 $V_{out}=I_{in}{R}_F\bullet [-g_m(R_F\parallel R_D)]$，即开环跨阻增益


  在这个电路图中，可以发现一个不一致，根据加载效应计算出来的环路增益为 $g_m(R_F\parallel R_D)$ ，如果直接将RF与M1栅极断开，求出的环路增益为 $g_m{R}_D$ ，这个不一致也将会影响通过开环参数对闭环参数的评估，可以预测，两个环路增益求出的闭环参数也将有所差别。关于两种方法的不一致，可以进行讨论，首先直接断环不考虑加载效应，这样的环路增益当然是不准确的，但是对于考虑加载效应的断开环路，在前文假设中可以知道，此方法假设信号是单向流动的，忽略的前馈网络中的反馈，以及反馈网络中的前馈，因此该方法也同样会产生误差，所以，两个结果的不一致，来源于模型近似的性质。

2.4电流-电流反馈的加载

  默认信号单向流动，忽略前馈网络的反馈和反馈网络的前馈。
  对于电流-电流反馈，前馈网络的输出为受控电流源，输入控制量为电流信号，因此适用于H模型；对于反馈网络，反馈网络的输出为受控电流源，输入控制量为电流信号，适用于H模型。电流-电流反馈的电路模型如图2.10所示。


  其 $H_{21}$ 为前馈网络的跨阻增益Rm，参考分析式（2.9），同理 ${\left(1+h_{22}{H}_{11}\right)}^{-1}$ 和 ${\left(1+h_{11}{H}_{22}\right)}^{-1}$ 分别对应开环结构输入端和输出端的分流器，则带有加载效应的开环放大器如图2.14所示。

  对于H模型，根据（2.3）可知。

  根据数学公式可知， $h_{11}$ 可以通过使反馈网络输出开路（I2=0）得到， $h_{22}$ 可以通过使反馈网络输入短路（V1=0）得到，如图2.14所示开环原理图。对反馈系数进行求解，反馈网路为H模型，因此反馈系数根据式（2.3）可知

  一个电流-电流反馈的电路图，如图2.15所示

  易得开环电流增益

  根据式（2.32），令V2=0，反馈网络输出电流与反馈网络输入电流之比即为反馈系数，正反向为灌入电压节点方向，即I2灌入V2为正方向，V2=0相当于从GND流进 $R_F$方向为正方向，因此

  因此可以得到闭环电流增益为

3.加载效应总结

  对于考虑加载效应的反馈环路，可以按照如下步骤进行求解：
  （1）断开含有完全加载的环路，计算开环增益 $A_{OL}$ 及开环输入和输出阻抗；
  （2）确定反馈系数β，得出环路增益 $\beta A_{OL}$
  （3）将开环的各个值通过比例因子 $1+\beta A_{OL}$ 的变化，计算闭环增益、输入和输出的阻抗。

  如图3.1，为四种典型反馈带加载的开环原理图，定义反馈系数 $\beta$ 的式子中，脚标1和2分别代表反馈网络的输入和输出端口。

  若不考虑加载效应，直接断开环路，环路增益如图3.2所示

  图3.2中环路增益可以表示为式（3.1）

  通过图3.2求得的环路增益，与通过图3.1得到的环路增益，会存在不一致，这个不一致也将会影响通过开环参数对闭环参数的评估，可以预测，两个环路增益求出的闭环参数也将有所差别。

  关于两种方法的不一致，可以进行讨论，首先直接断环不考虑加载效应，这样的环路增益当然是不准确的，但是对于考虑加载效应的断开环路，在前文假设中可以知道，此方法假设信号是单向流动的，忽略的前馈网络中的反馈，以及反馈网络中的前馈， 因此该方法也同样会产生误差，所以，两个结果的不一致，来源于模型近似的性质。

  对于反馈系统的求解，也可选择不断开环路的 “波特方法” 和 “麦德布鲁克方法” ，这两种方法，后续补充。

往期链接

      【模拟集成电路】反馈系统——基础到进阶（一）
      【模拟集成电路】反馈系统直接开环——基础到进阶（二）
      【模拟集成电路】反馈系统加载效应——基础到进阶（三）