经过了多层感知机后,相当于将原始的特征转化成了新的特征,或者说提炼出更合适的特征,这就是隐藏层的作用。
from:清晰理解多层感知机和反向传播 - 知乎
一、多层感知机的从零开始实现
import torch
from torch import nn
from d2l import torch as d2l
batch_size = 256 # 批量大小
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size) # 读取数据集
1.1 初始化模型参数
实现一个具有隐藏层的多层感知机,它包含256个隐藏单元。
# 初始化模型参数
num_inputs, num_outputs, num_hiddens = 784, 10, 256 # 输入特征数量,输出类别,隐藏单元
W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True) * 0.01) # 第一层的权重矩阵
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True)) # 第一层的偏置向量
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True) * 0.01) # 第二层的权重矩阵
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True)) # 第二层的偏置向量
params = [W1, b1, W2, b2] # nn.Parameter为需要优化的张量分配地址空间nn.Parameter()是PyTorch中用于定义可训练参数的类。在神经网络模型中,我们可以通过定义nn.Parameter()来创建需要优化的可训练的张量。
1.2 实现Relu函数
# 实现Relu激活函数
def relu(X):
a = torch.zeros_like(X)
return torch.max(X, a)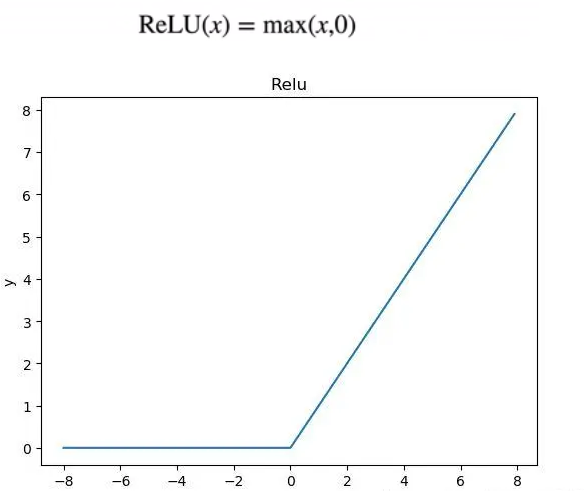
1.3 实现模型
# 实现模型
def net(X):
X = X.reshape((-1, num_inputs)) # 将图像拉伸为长度为num_inputs的向量
H = relu(X @ W1 + b1) # @为矩阵乘法,输出为长度为num_hiddens的向量,传入下一层
return (H @ W2 + b2)
loss = nn.CrossEntropyLoss() # 交叉熵损失1.4 训练
# 训练
num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr) # 定义优化算法
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)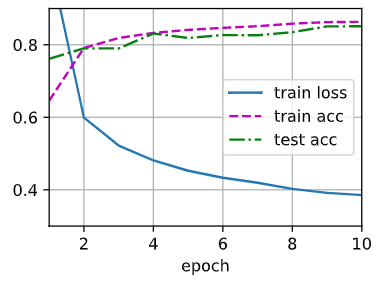
二、多层感知机的简洁实现
引用API更简洁实现多层感知机。
import torch
from torch import nn
from d2l import torch as d2l2.1 实现模型
# 实现模型
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 256), nn.ReLU(), nn.Linear(256, 10)) # 隐藏层有256个单元
def init_weights(m): # 初始化参数
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights)2.2 训练
# 训练
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none') # 交叉熵损失
trainer = torch.optim.SGD(net.parameters(), lr=lr) # 优化算法
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size) # 传入数据
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)