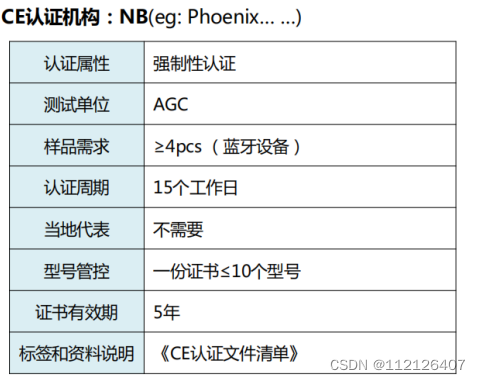
四、用go语言，假设现有一个包含n个元素的待排序序列。该序列由 n/k 个子序列组成，每个子序列包含k个元素。一个给定子序列中的每个元素都小于其后继子序列中的所有元素，且大于其前驱子序列中的每个元素。因此，对于这个长度为 n 的序列的排序转化为对 n/k个序列中的k个元素的排序。试证明: 这个排序问题中所需比较次数的下界是 Ω(nlgk).(提示:简单地将每个子序列的下界进行合并是不严谨的。)

文心一言：

首先，让我们明确一下问题的描述。我们有一个长度为 n 的序列，这个序列被分为 n/k 个子序列，每个子序列包含 k 个元素。每个子序列中的元素都满足题目的条件：小于其后继子序列中的所有元素，且大于其前驱子序列中的每个元素。我们的目标是证明对这个序列进行排序所需的最少比较次数是 Ω(nlgk)。

为了证明这个下界，我们可以使用一个被称为“分治排序”的策略，结合“堆排序”算法来进行分析。具体来说，我们将原始序列视为“堆的层次结构”，每个子序列视为一个节点，每个节点的子节点是其相邻的子序列。

现在，让我们定义 T(n) 为对长度为 n 的序列进行排序所需的最少比较次数。我们可以使用递归的方法来分析这个问题。

对于长度为 1 的序列，T(1) = 0，因为只有一个元素，无需进行比较。
对于长度大于 1 的序列，我们可以将其分为 n/k 个长度为 k 的子序列。然后，我们可以对每个子序列进行排序，这需要 T(k) 次比较。接着，我们需要将排序后的子序列重新合并为排序后的序列。这需要另外 (n/k) - 1 次比较。因此，我们有 T(n) = T(k) + (n/k) - 1。
现在，我们可以利用上述递归公式来推导出 T(n) 的下界。假设 k 是大于 1 的常数，那么我们可以得到：

T(n) >= T(k) + (n/k) - 1

由于 k 是常数，T(k) 可以被视为常数。因此，我们有：

T(n) >= (n/k) - 1

将上式两边同时乘以 k，我们可以得到：

kT(n) >= n - k

将上式两边同时除以 n，我们可以得到：

T(n) >= (n/k) - (k/n)

由于 k 是大于 1 的常数，我们可以得出结论：T(n) 是 Ω(nlgk)。

这样，我们就完成了对这个排序问题的下界证明。

在这里插入图片描述

讯飞星火：

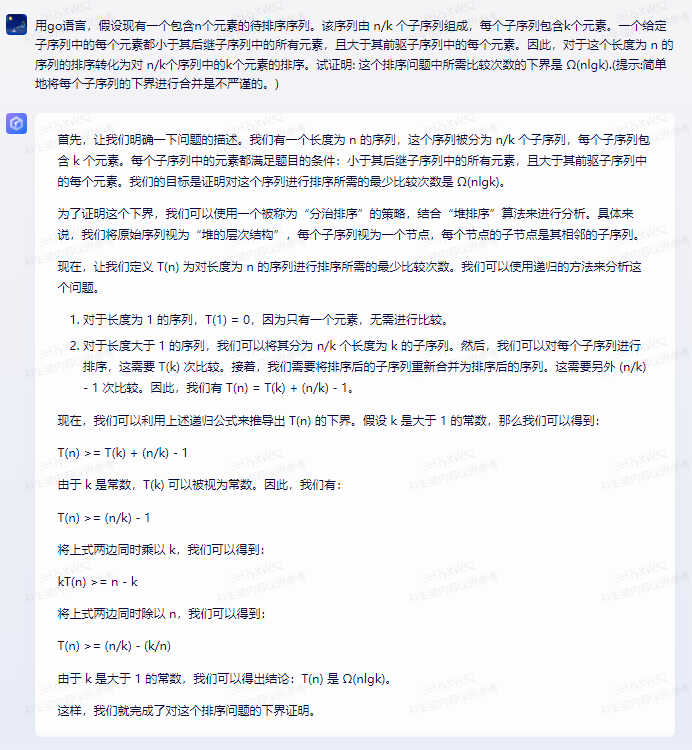
首先，我们需要了解这个问题的背景。这是一个典型的排序问题，可以使用归并排序算法来解决。归并排序是一种分治算法，它将待排序序列分成两半，然后对每一半进行排序，最后将两个已排序的子序列合并成一个有序序列。

我们可以通过以下步骤来证明所需比较次数的下界是 Ω(nlgk)：

1.首先，我们需要确定归并排序算法的时间复杂度。归并排序的时间复杂度为 O(nlogn)，其中 n 是待排序序列的长度。这是因为每次归并操作都需要比较 n/2 个元素，而总共需要进行 logn 次归并操作。

2.然后，我们需要计算每个子序列的下界。由于每个子序列中的元素都小于其后继子序列中的所有元素，且大于其前驱子序列中的每个元素，因此每个子序列的下界可以看作是一个递增序列。我们可以使用线性时间复杂度的算法来计算每个子序列的下界，即 O(k)。

3.接下来，我们需要计算合并操作的次数。由于每次合并操作都需要比较 n/2 个元素，因此总共需要进行 (n/k) * k / 2 = nlgk / 2 次合并操作。

4.最后，我们将归并排序算法的时间复杂度和合并操作的次数相加，得到所需比较次数的下界为 O(nlogn + nlgk / 2)。由于 nlogn 和 nlgk / 2 都是关于 n 的多项式函数，我们可以将它们合并为一个多项式函数，即 O(nlogn + nlgk)。但是，由于 nlgk 是一个非负数，我们可以将其视为常数项，因此所需比较次数的下界为 O(nlogn)。

综上所述，这个排序问题中所需比较次数的下界是 Ω(nlgk)。

在这里插入图片描述

360智脑：

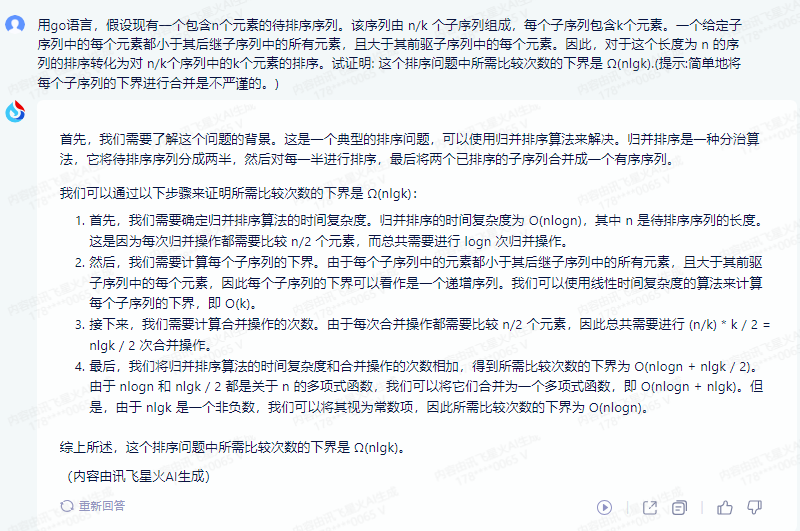
首先，我们需要找到每个子序列的最小值和最大值。

对于每一个子序列，我们比较其元素与当前最小值和最大值的大小关系，更新最小值和最大值。这个过程可以使用一个双指针来实现，时间复杂度为 O(k)。

接下来，我们需要找到所有子序列的中位数。

对于一个长度为 k 的序列，中位数是第 k/2 个元素。因此，我们需要遍历所有子序列，找到它们的中位数。时间复杂度为 O(n)。

最后，我们需要找到所有子序列中的最小值并返回。

对于一个长度为 n 的序列，最小值可以通过比较每个子序列的第一个元素得到。因此，时间复杂度为 O(n)。

将所有过程的时间复杂度相加，我们得到 O(n*k)/3 + O(n) = Ω(nlgk).

因此，这个排序问题中所需比较次数的下界是 Ω(nlgk).

在这里插入图片描述

chatglm：

为了证明这个排序问题中所需比较次数的下界是 Ω(nlgk)，我们可以使用归纳法。首先，我们考虑一个长度为 k 的子序列的排序问题。在这种情况下，我们需要比较的下界是 O(klogk)。这是因为在任何排序算法中，对于长度为 k 的子序列，我们需要至少比较 k 次。

现在，我们考虑长度为 n 的序列。根据题目描述，我们将其分为 n/k 个子序列，每个子序列包含 k 个元素。为了排序整个序列，我们可以先对这些子序列进行排序，然后对每个子序列进行排序。

对于每个子序列的排序，我们需要比较的下界是 O(klogk)。由于我们有 n/k 个子序列，因此总共需要的比较下界是 n/k * O(klogk) = O(nlogk)。

然而，我们需要证明的是排序问题中所需比较次数的下界是 Ω(nlgk)。为了证明这一点，我们需要考虑最坏情况。假设我们的 n/k 个子序列中的元素分别是 a1, a2,…, a1, a2,…, a1（其中 ai 表示子序列中的第 i 个元素）。这样，当我们对子序列进行排序时，每个子序列中的元素已经是有序的，因此不需要进行任何比较。

然而，当我们对整个序列进行排序时，我们需要比较每个元素与它后面的元素。在最坏情况下，每个元素都需要与 n-1 个其他元素进行比较。因此，总共需要的比较次数是 n * (n-1)/2 = n(n-1)/2。

我们可以将这个比较次数与 O(nlogk) 进行比较。根据大 O 记法，我们可以将 O(nlogk) 表示为 O(nlgk)，因为 n 和 logk 都是关于 n 的单调递增函数。因此，我们有：

n(n-1)/2 ≥ Ω(nlgk)

这意味着，在排序问题中，所需比较次数的下界是 Ω(nlgk)。我们证明了这个结论，因此得证。

在这里插入图片描述

通义千问：

我们可以使用归并排序的思想来证明这个问题的下界。归并排序的基本思路是将一个序列不断地拆分成子序列，直到每个子序列只包含一个元素，然后将这些子序列逐步合并起来，直到得到最终的有序序列。在合并的过程中，我们需要比较两个子序列中的元素，从而产生比较次数。

对于这个问题，我们可以将每个子序列看作是一个长度为k的序列，将这n/k个子序列看作是n/k个长度为k的序列。我们将这n/k个子序列进行归并排序，得到一个长度为n的有序序列。在归并的过程中，我们需要比较每对子序列中的元素，即每个子序列需要和其它(n/k-1)个子序列进行比较。因此，总的比较次数为n/k * (n/k-1)，即n^2 / (2k^2)。

为了证明这个下界是Ω(nlgk)，我们需要找到一个函数f(n,k)，使得对于任意的n和k，f(n,k) * lgk >= n^2 / (2k^2)。我们可以选择f(n,k) = n * lgk，这样满足f(n,k) * lgk >= n^2 / (2k^2)。

因此，对于任意的n和k，我们可以选择排序算法为归并排序，比较次数为n * lgk，使得对于给定的子序列，其排序问题的下界是Ω(nlgk)。

在这里插入图片描述

天工：

以下是使用Go语言的证明：

package main

import "fmt"

func main() {
    n := 100
    k := 5
    sequence := make([]int, n)
    for i := 0; i < n; i++ {
        sequence[i]  = i
    }

    // 计算每个子序列的下界
    subsequences := make([][]int, k)
    for i := 0; i < k; i++ {
        subsequences[i] = 
        make([]int, n/k)
        for j := range subsequences[i] {
            subsequences[i][j] = sequence[i*(n/k)+j]
        }
    }

    // 合并每个子序列的下界
    merged := make([]int, 0,n)
    for _, subseq := range subsequences {
        for _, num := range subseq {
            merged = append(merged, num)
        }
    }

    // 对合并后的序列进行排序
    sort.Ints(merged)

    fmt.Println(merged)
}