差分约束

前置知识: 最短路问题、SPFA判环，为了保证学习效果，请保证已经掌握前置知识之后，再来学习本章节！

引出

当我们遇到一个不等式组，比如下面这个

\begin{cases} x_{1}-x_{3} \leq 5 \\ x_{1}-x_{2} \leq 2 \\ x_{2}-x_{1} \leq 0 \\ x_{2}-x_{3} \leq 2 \\ x_{3}-x_{2} \leq-1 \\ x_{3}-x_{1} \leq -2 \end{cases}⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧x1−x3≤5x1−x2≤2x2−x1≤0x2−x3≤2x3−x2≤−1x3−x1≤−2
怎么进行求解？

我们可以很容易地想到：

给其中一个变量赋一个具体的值，然后再逐渐估测其他变量的值，并不断修改。

比如：

先给 x_{1}x1 任意赋一个值，比如令 x_{1}=0x1=0，之后根据 x_{1}-x_{3} \leq 5x1−x3≤5，x_{1}-x_{2} \leq 2x1−x2≤2 ，令 x_3=-5,x_2=-2x3=−5,x2=−2，又因为 x_{2}-x_{1} \leq 0,x_{3}-x_{1} \leq -2x2−x1≤0,x3−x1≤−2，发现这组解满足条件。
根据 x_{2}-x_{3} \leq 2x2−x3≤2，x_3x3 改为 -4−4。
发现 x_{3}-x_{2} \leq-1x3−x2≤−1 也满足条件
解得，x_1=0,x_2=-1,x_3=-4x1=0,x2=−1,x3=−4 为其中一组解。

然而，这样的方法只适合于规模较小的时候，而且是在猜的基础上的，这样也没有办法来解出题目。

我们观察下这些不等式，像在最短路里的三角不等式，于是，发现了这些性质：

我们设 disdis 数组代表长度，跟最短路里的 disdis 概念一样。

dis_v \leq dis_u+w(u \rightarrow v) \iff dis_v-dis_u \leq w(u \rightarrow v)disv≤disu+w(u→v)⟺disv−disu≤w(u→v)
所以，我们只要对于每个不等式 x_i-x_j \leq yxi−xj≤y，连一条从 jj 到 ii 长度为 yy 的边，跑一遍最短路，即可得到一组解。

备注：我们设 cntcnt 数组来表示这个点记录了几次，如果这个图有负环，说明 cnt_i \geq ncnti≥n，则要输出无解。

这就是差分约束算法的重要思想。

差分约束

差分约束定义

差分约束（Difference-Constraints），即给出对 nn 个未知数，mm 组形如 x_{c_k}-x_{c'_k}\leq y_kxck−xck′≤yk 的约束不等式，形如
\begin{cases} x_{c_1}-x_{c'_1}\leq y_1 \\ x_{c_2}-x_{c'_2} \leq y_2 \\ \cdots\\ x_{c_m}-x_{c'_m}\leq y_m\end{cases}⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧xc1−xc1′≤y1xc2−xc2′≤y2⋯xcm−xcm′≤ym

的不等式组，其中，y_kyk 是常数（可以是非负数，也可以是负数）。

我们要解决的问题是：求一组解 x_1=a_1,x_2=a_2,...,x_n=a_nx1=a1,x2=a2,...,xn=an，使得所有的约束条件得到满足，否则判断出无解。

差分约束系统的定义

如果一个系统由 nn 个变量 a_1,a_2,\cdots,a_na1,a2,⋯,an 和 mm 个约束条件组成，每个约束条件均为形如 a_i−a_j≤kai−aj≤k 的不等式（i,j \in [1,n]i,j∈[1,n]，kk 为常数），则称其为 差分约束系统。

换句话说，差分约束系统是 求解关于一组变量的特殊不等式组 的方法。

差分约束与图上最短路问题的关系

假设图上给定两点 ii 和 jj，它们之间有一条从 jj 指向 ii 的有向边，边权为 cc，且 图上不存在负环。那么， 对于该条边，在求完最短路之后，必然有：
dis[i] \leq dis[j] + cdis[i]≤dis[j]+c
否则，说明有的节点的最短距离没有更新，不是最短的。

对于图中的任意一条边，都必然会满足这样一个不等式。因此，如果我们将差分约束的不等式组中的每个不等式 x_i - x_j \leq c_kxi−xj≤ck 都看作一条 j\xrightarrow{c_k}ijcki 的边。 将解不等式组的问题转化成图上的问题。

那么，对于这样的一张图，我们选取一个可以走完所有边的源点。从该源点出发，求一次单源最短路后，dis[]dis[] 数组也就同时满足该差分约束的不等式组了。换句话说，最短距离数组 dis[]dis[] 是该差分约束系统的一组可行解。

然而，该不等式组转化后的图可能是不连通的，因此，我们可以设一个超级源点 x_0x0，其 dis[0]=0dis[0]=0，同时将它和其他所有节点都连一条权重为 00 的有向边，这样就能保证可以遍历所有边了。

负环与差分约束无解

如果图上存在负环的话，对应的差分约束不等式组是无解的。

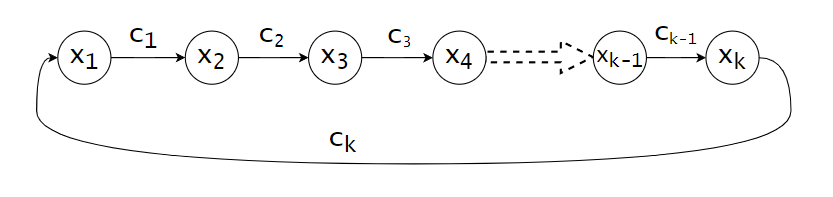
假设图中存在负环，比如上图中的负环，因为是负环，所以有：
\sum_{i=1}^k c_i = c_1+c_2+c_3+\cdots + c_{k-1} + c_k < 0i=1∑kci=c1+c2+c3+⋯+ck−1+ck<0
又因为该图对应的边为差分约束中的不等式，所以有：
\begin{cases}x_2\leq x_1 + c_1\\x_3\leq x_2 + c_2\\x_4\leq x_3 + c_3\\\cdots\\x_k\leq x_{k-1} + c_{k-1}\\x_1\leq x_k + c_k \end{cases}⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧x2≤x1+c1x3≤x2+c2x4≤x3+c3⋯xk≤xk−1+ck−1x1≤xk+ck
对上面不等式组进行组合，并放缩，则有：
x_2\leq x_1 + c_1\\\leq x_k + c_k + c_1\\\leq x_{k-1} + c_{k-1} + c_k + c_1\\\leq x_{k-2} + c_{k-2} + c_{k-1} + c_k + c_1\\\cdots\\\leq x_2 + c_2 + c_3 + \cdots + c_{k-1} + c_k + c_1\\\leq x_2 + \sum_{i=1}^k c_ix2≤x1+c1≤xk+ck+c1≤xk−1+ck−1+ck+c1≤xk−2+ck−2+ck−1+ck+c1⋯≤x2+c2+c3+⋯+ck−1+ck+c1≤x2+i=1∑kci
也就是：
x_2\leq x_2 + \sum_{i=1}^k c_ix2≤x2+i=1∑kci

当图中含有负环时， \sum_{i=1}^k c_i < 0∑i=1kci<0 ，上式必然无解。因此，如果图上存在负环的话，对应的差分约束不等式组必然无解。

差分约束的求解方法

差分约束问题可以转化为最短路 / 最长路问题解决。我们有如下结论（证明详见后面）：

如果求的是最小值，则应该将问题转化为最长路问题
如果求的是最大值，则应该将问题转化为最短路问题

差分约束系统和图上最短路问题的关系我们已经了解，因此，我们使用图来对差分约束系统建模。

转化为最短路问题

我们把每个变量 x_ixi 看做图中的一个结点，对于每个约束条件 x_i-x_j\leq c_kxi−xj≤ck ，我们对其进行如下转化：
x_i-x_j\leq c_k \iff x_i\leq x_j + c_kxi−xj≤ck⟺xi≤xj+ck
相应地，转化为图上问题时，我们从 结点 jj 向结点 ii 连一条权值为 c_kck 的有向边，然后在此图上求解差分约束，具体步骤为：

建立 nn 个顶点，mm 条边的有向图，对于约束条件 x_i-x_j\leq c_kxi−xj≤ck 建立一条 j\rightarrow ij→i 的边，权值为 c_kck；
设超级源点 dis[0]=0dis[0]=0 并向每一个点连一条权重为 00 边；(我们并不是一定要建一个超级源点，如果我们可以找到一个节点，从它出发可以遍历所有边，那么也可以从它出发跑单源最短路)
从上面选取的源点出发，跑单源最短路；
结果分情况讨论：（1）若图中存在负环，则给定的差分约束系统无解。（2）如果没有负环，则 dis[1]\sim dis[n]dis[1]∼dis[n] 就是一组可行的解。

又因为可能存在负边权，所以这里最好用 SPFASPFA 或 Bellman-FordBellman−Ford 跑，不能用 dijkstradijkstra。

转化为最长路问题

和转化为最短路问题，对称地，我们也可以把差分约束问题转化为图上的最长路问题，求得的解也是原问题的一组可行解。

和转为最短路不同的是，我们对不等式进行如下转化：
x_i-x_j\leq c_k \iff x_j \geq x_i +(- c_k)xi−xj≤ck⟺xj≥xi+(−ck)
相应地，转化为图上问题时，我们从 结点 ii 向结点 jj 连一条权值为 -c_k−ck 的有向边，然后在此图上求解差分约束，具体步骤为：

建立 nn 个顶点，mm 条边的有向图，对于约束条件 x_i-x_j\leq c_kxi−xj≤ck 建立一条 i\rightarrow ji→j 的边，权值为 -c_k−ck；
设超级源点 dis[0]=0dis[0]=0 并向每一个点连一条权重为 00 边；(我们并不是一定要建一个超级源点，如果我们可以找到一个节点，从它出发可以遍历所有边，那么也可以从它出发跑单源最短路)
从上面选取的源点出发，跑单源最长路；
结果分情况讨论：（1）若图中存在正环，则给定的差分约束系统无解。（2）如果没有正环，则 dis[1]\sim dis[n]dis[1]∼dis[n] 就是一组可行的解。

跑最长路问题，可以用 SPFASPFA 或拓扑排序

注意到，如果我们求出 \{a_1,a_2,...,a_n\}{a1,a2,...,an} 是该差分约束系统的一组解，那么对于任意的常数 dd ， \{a_1+d,a_2+d,...,a_n+d\}{a1+d,a2+d,...,an+d} 显然也是该差分约束系统的一组解，因为这样做差后 dd 刚好被消掉。因此， 一个差分约束系统，要么无解，要么有无数组解。

应用一、求不等式组的可行解

即上面描述的解不等式组的问题，例题：差分约束 - TopsCoding

对于这类不等式组的求解，我们可以将其抽象成一个有 nn 个点的最短路问题，对于不等式 x_i-x_j \leq yxi−xj≤y，建一条从 jj 连向 ii 边权为 yy 的单向边。

建完图后，为了避免图不连通，导致有些点的距离不会更新的问题，我们可以新建一个超级源点 s=0s=0 向每个点连出一条边权为 00 的边。

如果建好图后，图中不存在负环，那么，原不等式组就有解，否则存在负环，就说明原不等式无解。

于是就很容易地做出来这模板题了。

#include<bits/stdc++.h>
using namespace std;
int n,m,fir[5005],tot;
struct edge
{
    int nxt,to,val;
}e[10005];
int dis[5005],cnt[5005];
bool vis[5005];

void add(int u,int v,int w)
{
    e[++tot]={fir[u],v,w};fir[u]=tot;
}

bool SPFA(int s)
{
    queue<int>q;
    memset(dis,0x3f,sizeof dis);
    dis[s]=0;
    vis[s]=1;
    q.push(s);
    while(!q.empty())
    {
        int u=q.front();q.pop();
        vis[u]=0;
        for(int i=fir[u];i;i=e[i].nxt)
        {
            int v=e[i].to;
            if(dis[v]>dis[u]+e[i].val)
            {
                dis[v]=dis[u]+e[i].val;
                cnt[v]++;
                if(cnt[v]==n+1) return 0;  // 有负环，无解    注意，添加了一个超级源点
                if(vis[v]==0)
                {
                    vis[v]=1;
                    q.push(v);
                }
            }
        }
    }
    return 1;
}

int main()
{
    scanf("%d%d",&n,&m);
    int s=0;
    for(int i=1;i<=m;i++)
    {
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        add(v,u,w);
    }
    // 添加 0 号节点，指向 1~n 号节点，边权为 0
    for(int i=1;i<=n;i++)  add(s,i,0);
    if(!SPFA(s))
    {
        cout<<"NO";  // 有负环
        return 0;
    }
    // dis[] 就是一组可行的解
    for(int i=1;i<=n;i++)
        cout<<dis[i]<<" ";
    return 0;
}

Copy

应用二、求最值问题

给定若干约束不等式，即：
\begin{cases} x_{c_1}-x_{c'_1}\leq y_1 \\ x_{c_2}-x_{c'_2} \leq y_2 \\ \cdots\\ x_{c_m}-x_{c'_m}\leq y_m\end{cases}⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧xc1−xc1′≤y1xc2−xc2′≤y2⋯xcm−xcm′≤ym
同时，对于每个或其中若干个变量 x_ixi，约定其下界和上界（k\leq nk≤n）：
\begin{cases} L_1\leq x_1 \leq R_1\\ L_2\leq x_2 \leq R_2\\ \cdots\\ L_k\leq x_k \leq R_k\end{cases}⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧L1≤x1≤R1L2≤x2≤R2⋯Lk≤xk≤Rk
在上述约束条件下，求所有可行解中， x_ixi 的最小值或者最大值。

形式一、求最大值

此时，问题模型中，可能是对 x_ixi 约束了一个上界，x_i\leq R_ixi≤Ri，求 x_ixi 的最大值。

我们考虑所有从 x[i]x[i] 出发，构成的不等式链，对于任意一条不等式链，如果想稳定下来，最终都要在节点 x_0x0 处停止，形如：
x[i] ≤ x[j] + c[j] \\≤ x[k] + c[k] + c[j]\\≤ x[0] + c[1]+ c[2]+... + c[j] \\= 0 + c[1]+ ... + c[j]x[i]≤x[j]+c[j]≤x[k]+c[k]+c[j]≤x[0]+c[1]+c[2]+...+c[j]=0+c[1]+...+c[j]
因此，所有链对应到图上，都是从 00 点出发，到 ii 号节点的一条路径。所以，最终的上界组为：
\begin{cases} x_i\leq x_0 + s_1\\ x_i\leq x_0 + s_2\\ \cdots\\ x_i\leq x_0 + s_m \end{cases}⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧xi≤x0+s1xi≤x0+s2⋯xi≤x0+sm

上式中， mm 为从 00 到 ii 的路径的条数，ss 为对应路径的权值的和（即路径长度）。最终 x[i]x[i] 的最大值为所有上界的最小值，因此，求最大值问题可以转为图上的 求解最短路问题。

具体求法，上面已经做了详细分析，这里不再多加描述。