常用代码模板2——基础算法

构思算法：可以先想暴力解法，然后观察时间复杂度，如果超时，再考虑优化，优化的方向就是时间复杂度要下降，下表可以给出一些算法选择的参考：

暴力枚举 -> 枚举+优化 -> 正解

数据范围	时间复杂度	考察的算法
n \leq 30n≤30	指数级别	dfs+剪枝，状态压缩dp
n\leq10^2n≤102	O(n^3)O(n3)	floyd，dp
n\leq10^3n≤103	O(n^2),O(n^2\log n)O(n2),O(n2logn)	dp，二分，朴素版Dijkstra，朴素版Prim，Bellman-Ford
n\leq10^4n≤104	O(n*\sqrt{n})O(n∗n)	块状链表，分块，莫队
n\leq10^5n≤105	O(n\log n)O(nlogn)	各种sort，线段树，树状数组，set/map，heap，拓扑排序，dijkstra+heap，prim+heap，spfa，二分
n\leq10^6n≤106	O(n)O(n),常数较小的 O(n\log n)O(nlogn)算法	hash，双指针扫描，并查集，常数较小的 O(n\log n)O(nlogn)算法：sort，树状数组，ST表，heap，dijkstra，spfa
n\leq10^7n≤107	O(n)O(n)	双指针扫描，线性筛素数
n\leq10^9n≤109	O(\sqrt{n})O(n)	判断质数
n\leq10^{18}n≤1018	O(\log n)O(logn)	最大公约数，快速幂
n\leq10^{1000}n≤101000	O((\log n)^2)O((logn)2)	高精度加减乘除

备注：\log nlogn 主要出现在二分、分治和树、图中。

素数判定

试除法

// 试除法：判断一个整数 i 是不是素数，是则返回 true，否则返回 false
bool isprime(int i){
    if(i < 2)
        return false;
    for(int j = 2; j <= sqrt(i); j++)
        if(i % j == 0)
            return false;
    return true;
}

Copy

埃氏筛法

const int N = 100000;   // N 的大小取决于问题中 n 的范围
bool a[N];   // 标记数组  a[i] = 0(false):素数，a[i]=1(true): 非素数
// 埃氏筛法 函数执行完后 a[] 数组即为筛出的素数结果 a[i]=false 表示 i 是素数
void prime()
{
    a[0]=a[1]=true;         // 0 和 1 不是素数
    for(int i = 2; i <= n; i++)
    {
        if(a[i] == false)   // i 是素数
        {
            for(int j = i+i; j <= n; j += i)
                a[j] = true;
        }
    }
}

Copy

例题：素数距离 - TopsCoding

质因数分解

int t = 2;
while(k!=1){
    while(k%t == 0) {
        k /= t;
        cout << t << ' ';
    }

    t++;
}

Copy

递推

数学中的斐波那契数列、错排问题的递推公式、等差数列、等比数列问题，都可以用递推去解决。

在编程中，计算问题的解时，如果可以找到前后过程之间的数量关系（即递推式），那么就可以用递推去解决。
f[i] = g(f[i-1],f[i-2],...,f[1])f[i]=g(f[i−1],f[i−2],...,f[1])

int f[N] = {部分初始值};
for(int i = 2; i <= n; i++)
{
    f[i] = ...f[i-1]...f[i-2]...;
}
cout << f[n];

Copy

例题：小 C 的数组（array） - TopsCoding

逆序对

冒泡排序

时间复杂度：O(n^2)O(n2)

适用场景：数据范围不大时，可用来求逆序对

模板题：求逆序对个数I - TopsCoding

int n, a[N], cnt = 0;
for(int i=0; i<n; i++)
{
    for(int j=0; j<n-i; j++)
    {
        if(a[j]>a[j+1]) {
            swap(a[j], a[j+1]);  //交换数据，同时也意味着存在一个逆序对
            cnt++;   // 逆序对++
        }
    }
}

Copy

归并排序

时间复杂度：O(n\log n)O(nlogn)

适用场景：数据范围较大时，可用来求逆序对

模板题：求逆序对个数II - TopsCoding

int n, a[N], tmp[N];   // tmp 数组用来保存中间排序结果
int cnt = 0;   // 逆序对个数

void merge_sort(int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1;
    merge_sort(l, mid);        // 排序左半部分
    merge_sort(mid + 1, r);    // 排序右半部分

    // 合并左右子数组
    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r) {
        if (a[i] <= a[j]) {
            tmp[k++] = a[i++]; 
        }
        else {
            tmp[k++] = a[j++];
            cnt += mid-i+1; // a[i]>a[j],必然有a[i]~a[mid]>a[j],有 mid-i+1 对
        }
    }
    while (i <= mid) tmp[k++] = a[i++];
    while (j <= r) tmp[k++] = a[j++];
    for (i = l, j = 0; i <= r; i++, j++) a[i] = tmp[j];
}

Copy

快速幂*

求 m^k%pmk，时间复杂度 O(\log k)O(logk)。

// 递归写法
int qmi(int m, int k, int p) {
    if (k == 0) return 1;
    if (k & 1) {
        return m * qmi(m, k-1, p) % p;
    }
    else {
        int t = qmi(m, k>>1, p);
        return t * t % p;
    }
}

// 迭代写法
int qmi(int m, int k, int p)
{
    int res = 1 % p, t = m;
    while (k)
    {
        if (k&1) res = res * t % p;
        t = t * t % p;
        k >>= 1;
    }
    return res;
}

Copy

二分答案

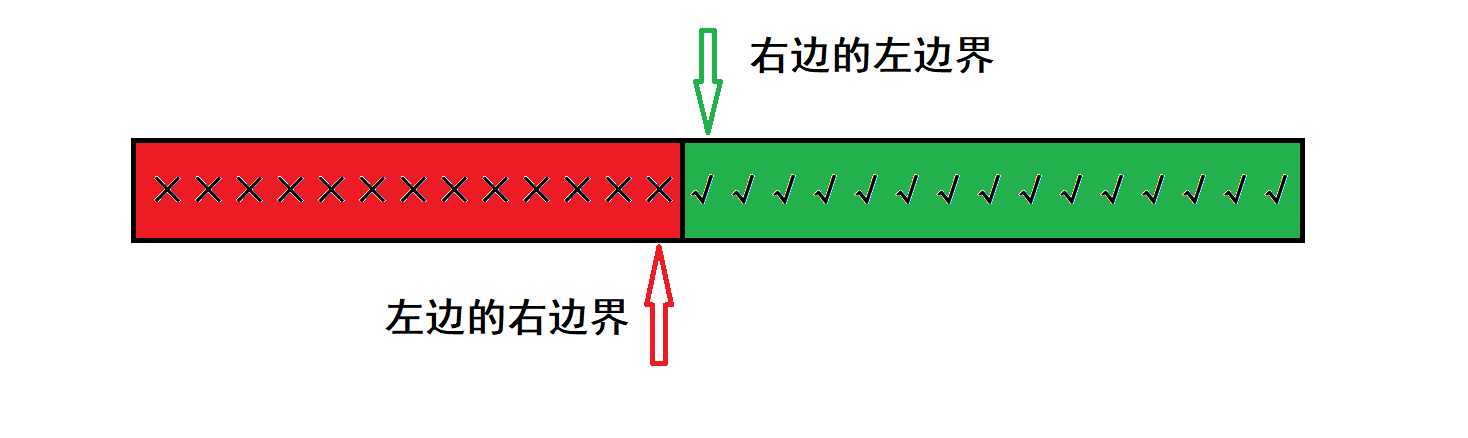
int l = MIN, r = MAX, mid, ans;
while(l <= r) {
    mid = (l + r) / 2;
    if(check(mid)) {
        ans = mid;      // 记录当前最优解
        l = mid + 1;    // 看是找哪边，继续去搜 左半/右半 区间
        // or r = mid - 1;
    } else {
        r = mid - 1;
        // or l = mid + 1;
    }
}
cout << ans << endl;

Copy

例题：

木板打地鼠 - TopsCoding
游戏闯关 - TopsCoding

一维前缀和

二维前缀和

贪心

所谓贪心算法是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的仅是在某种意义上的局部最优解。

贪心算法一般按如下步骤进行：①建立数学模型来描述问题。②把求解的问题分成若干个子问题。③对每个子问题求解，得到子问题的局部最优解。④把子问题的解局部最优解合成原来解问题的一个解。

一般会用到排序，或优先队列，没有固定的代码模板。

区间贪心

区间类贪心一般会要求对若干个区间进行筛选。解题思路一般为：

先对区间按照左端点从小到大，右区间从大到小进行排序（方便对区间进行遍历）；
遍历区间，贪心选取一些区间，一般会用到指针变量。

例题：区间覆盖 - TopsCoding

BFS

即按层逐个遍历，适合求解最短路类问题，尤其是图上的最短路问题（最短路类问题用 dfs 在大数据量下很容易超时）。代码框架如下：

全局状态变量

void bfs(初始状态)
{
    定义状态队列
    初始状态入队
    while(队列不为空)
    {
        取出队首状态作为当前状态
        if(当前状态是目标状态) {
            进行相应处理（输出当前解、更新最优解、退出返回等） 
            return ;
        }
        for(所有可行的新状态)   
        {
            if(新状态没有访问过 && 需要访问)  // 可行性剪枝、最优性剪枝、重复性剪枝
            {
                新状态入队
            }
        }
}

Copy

练习题：

抓牛(catchcow) - TopsCoding
瓷砖 - TopsCoding
单词接龙 II - TopsCoding
老子的意大利炮呢 - TopsCoding

DFS

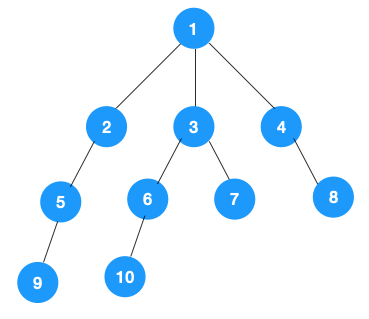
全局状态变量

void/int dfs(当前状态)
{
    if(当前状态是目标状态)    // 判断
    {
         进行相应处理（输出当前解、更新最优解、退出返回等）   
    }
    for(所有可行的新状态)   // 扩展
    {
        if(新状态没有访问过 && 需要访问)  // 可行性剪枝、最优性剪枝、重复性剪枝
        {
            标记 
            dfs(新状态);
            取消标记       // 回溯
        }
    }
}
                
int main()
{
    ...
    dfs(初始状态);
    ...
}

Copy

易错点：需要注意的是，定义 dfs() 函数前一定要先考虑清楚，函数是否需要有返回值！如果定义了带返回值，但是函数中未写return，则会爆零！

剪枝

可行性剪枝：在搜索过程中，一旦发现如果某些状态无论如何都不能找到最终的解，就可以将其“剪枝”了，比如越界操作、非法操作。一般通过条件判断来实现，如果新的状态节点是非法的，则不扩展该节点

重复性剪枝：对于某一些特定的搜索方式，一个方案可能会被搜索很多次，这样是没必要的。在实现上，一般通过一个记忆数组来记录搜索到目前为止哪些状态已经被搜过了，然后在搜索过程中，如果新的状态已经被搜过了，则不再扩展该状态节点。

最优性剪枝：对于求最优解的一类问题，通常可以用最优性剪枝，比如在求解迷宫最短路的时候，如果发现当前的步数已经超过了当前最优解，那从当前状态开始的搜索都是多余的，因为这样搜索下去永远都搜不到更优的解。通过这样的剪枝，可以省去大量冗余的计算，避免超时。在实现上，一般通过一个记忆数组来记录搜索到目前为止的最优解，然后在搜索过程中，如果新的状态已经不可能是最优解了，那再往下搜索肯定搜不到最优解，于是不再扩展该状态节点。

练习题：

全排列问题 - TopsCoding
素数环 - TopsCoding
迷宫问题 - TopsCoding
细胞 - TopsCoding

记忆化搜索

每次搜索前先判断是否搜索过：

如果搜过，就直接返回之前存储的结果
否则搜索，并在返回之前将当前状态保存下来

int f[][][];

int dfs(状态列表)
{
    if(f[][][]) return f[][][];    // 避免重复搜索
    if(边界状态) {
        return f[][][] = ......;
    }
    int ans = ...;
    for(新状态) {
        ans = max/min(dfs(...), ans);
    }
    return f[][][] = ans;     // 返回前先保存
}

Copy

拓展：记忆化搜索和递推型动态规划联系紧密。如果碰到一些动规类型的题目，想不出怎么写时，可以考虑用记忆化搜索去解决。

练习题：

滑雪 - TopsCoding
搭积木(block) - TopsCoding
汉诺塔 V - TopsCoding

高精度加法

模板题：A+B Problem（高精度加法）

#include <bits/stdc++.h>
using namespace std;

string add(string a, string b)
{
    string ans;
    // 翻转，使个位在前
    reverse(a.begin(), a.end());
    reverse(b.begin(), b.end());
    // 预处理，方便后面按位相加
    a.push_back('0');  b.push_back('0');
    if(a.size() < b.size()) swap(a, b);
    // 短的数字高位补零
    while(b.size() < a.size()) b.push_back('0');
    // 按位累加，模拟加法
    int c[1000]={0}, k = a.size();
    for(int i = 0; i < a.size(); i++)
    {
        int s = c[i] + a[i]-'0' + b[i] - '0';
        c[i] = s%10;
        c[i+1] += s/10;
    }
    // 去除高位零
    while(c[k]==0 && k>=0) k--;
    // 输出
    while(k >= 0)
        ans.push_back(c[k--]+'0');
    return ans;
}

int main()
{
    string a, b;
    cin >> a >> b;
    cout << add(a, b);
    return 0;
}

Copy

更简洁的写法：

string add(string a, string b) {
    string c;
    reverse(a.begin(), a.end());
    reverse(b.begin(), b.end());
    int t = 0;
    for (int i = 0; i < a.size() || i < b.size(); i++) {
        if (i < a.size()) t += a[i] - '0';
        if (i < b.size()) t += b[i] - '0';
        c.push_back(t % 10 + '0');
        t /= 10;
    }
    if (t) c.push_back(t % 10 + '0');
    reverse(c.begin(), c.end());
    return c;
}

Copy

高精度减法

模板题：A-B Problem（高精度减法）

#include<bits/stdc++.h>
#include<algorithm>
using namespace std;

const int N = 1e6+5;

string sub(string a, string b)
{
    string ans;
    bool flag = false;
    if(a.size() < b.size() || (a.size()==b.size() && a < b))
    {
        swap(a, b);
        flag = true;    
    }
    // 翻转，使个位在前
    reverse(a.begin(), a.end());
    reverse(b.begin(), b.end());
    // 预处理，方便后面按位相减
    a.push_back('0');  b.push_back('0');
    if(a.size() < b.size()) swap(a, b);
    // 短的数字高位补零
    while(b.size() < a.size()) b.push_back('0');
    // 按位相减，模拟减法
    int c[1000]={0}, k = a.size();
    for(int i = 0; i < a.size(); i++)
    {
        if(a[i] < b[i]) a[i]+=10, a[i+1]--;
        c[i] = a[i] - b[i];
    }
    // 去除高位零
    while(c[k]==0 && k>=0) k--;
    // 输出
    if(flag) ans.push_back('-');
    while(k >= 0)
        ans.push_back(c[k--]+'0');
    return ans;
}

int main()
{
    ios::sync_with_stdio(false);
    string a, b;
    cin >> a >> b;
    string c = sub(a,b);
    cout << c;
    return 0;
}

Copy

高精度乘法

模板题：A*B Problem（高精度乘法）

#include<bits/stdc++.h>
#include<algorithm>
using namespace std;

const int N = 1e6+5;

string div(string a, string b)
{
    string ans;
    // 翻转，使个位在前
    reverse(a.begin(), a.end());
    reverse(b.begin(), b.end());
    // 按位相乘，模拟乘法
    int c[1000]={0}, k = a.size()+b.size()+1;
    for(int i = 0; i < a.size(); i++)
        for(int j = 0; j < b.size(); j++)
        {
            c[i+j] += (a[i]-'0')*(b[j]-'0');  // 乘，写上去
            c[i+j+1] += c[i+j]/10;      // 进位
            c[i+j] %= 10;       // 保留个位
        }
    // 去除高位零
    while(c[k]==0 && k>=0) k--;
    // 输出
    while(k >= 0)
        ans.push_back(c[k--]+'0');
    return ans;
}

int main()
{
    ios::sync_with_stdio(false);
    string a, b;
    cin >> a >> b;
    string c = div(a,b);
    cout << c;
    return 0;
}

Copy

高精度除法

模板题：A/B Problem（高精度除法）

#include <bits/stdc++.h>
using namespace std;

string div(string a, long long b)
{
    // z 数组保存计算结果
    int z[256] = {0}, d = 0;  // d 存余数
    // 计算相除
    for(int i = 0; i < a.size(); i++)
    {
        d = 10*d + a[i] - '0';   // 当前位拿下来
        z[i] = d / b;            // 商写上去
        d %= b;                  // 更新余数
    }
    
    // 处理计算结果
    string ans;   // 作为返回值
    int len = 0;
    while(z[len] == 0 && len < a.size()-1)    // 去掉高位的0
        len++;
    for(int i = len; i < a.size(); i++)
        // 将结果放到 ans 字符串中，如果
        ans.push_back(z[i]+'0');
    return ans;
}       

int main()
{
    string a;
    long long b;
    cin >> a >> b;
    cout << div(a, b);
    return 0;
}

Copy