转置卷积

计算输出的形状公式

输出矩阵的高 = (输入的高-1) x 高方向的步长 - 2 x 高方向的填充 + 卷积核的高
输出矩阵的宽 = (输入的宽-1) x 宽方向的步长 - 2 x 宽方向的填充 + 卷积核的宽

举例计算：当输入为2x2，转置卷积核形状为2x2的情况

代入公式验证输出形状：

输出矩阵的高 = (输入的高-1) x 高方向的步长 - 2 x 高方向的填充 + 卷积核的高
= （2-1)x1 - 2x0 + 2 = 1 +2 = 3

输出矩阵的宽 = (输入的宽-1) x 宽方向的步长 - 2 x 宽方向的填充 + 卷积核的宽
 = （2-1)x1 - 2x0 + 2 = 1 +2 = 3

举例计算：当输入为2x2，步幅为2，转置卷积核形状为2x2的情况

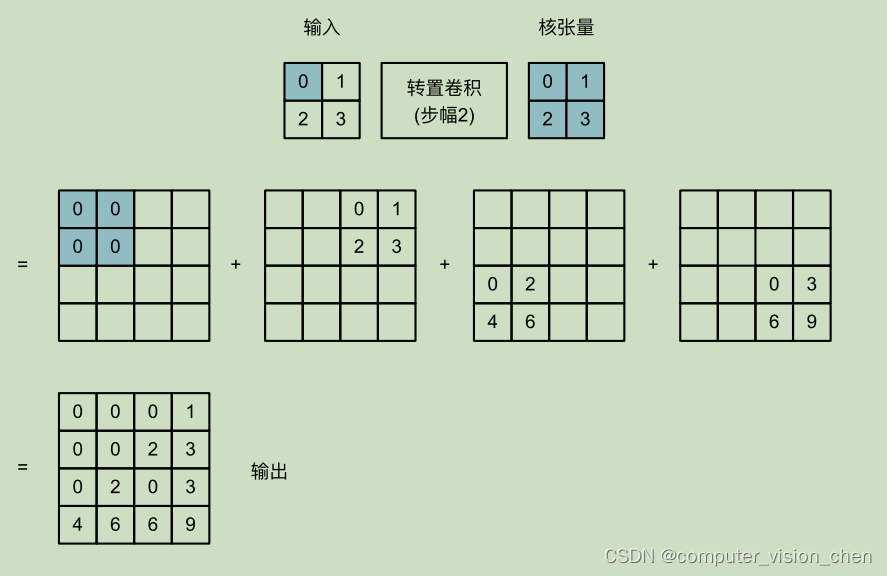
代入公式验证输出形状

输出矩阵的高 = (输入的高-1) x 高方向的步长 - 2 x 高方向的填充 + 卷积核的高
= （2-1)x2 - 2x0 + 2 = 2 + 2 = 4

输出矩阵的宽 = (输入的宽-1) x 宽方向的步长 - 2 x 宽方向的填充 + 卷积核的宽
 = （2-1)x2 - 2x0 + 2 = 2 + 2 = 4

转置卷积代码实现

import torch
from torch import nn
from d2l import torch as d2l

X = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
X, K = X.reshape(1, 1, 2, 2), K.reshape(1, 1, 2, 2) # 前两个元素是 样本数，通道数

# 下面函数的前两个元素是输入通道和输出通道数
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, stride=2, bias=False)
tconv.weight.data = K
output = tconv(X)
print(output,output.shape)

tensor([[[[0., 0., 0., 1.],
          [0., 0., 2., 3.],
          [0., 2., 0., 3.],
          [4., 6., 6., 9.]]]], grad_fn=<SlowConvTranspose2DBackward>) torch.Size([1, 1, 4, 4])

转置卷积的作用

对卷积层下采样得到的特征图进行转置卷积可以得到与输入图像相同的图像，可以应用于语义分割。
如:

输入图像： (样本数为1，通道为10，h=16,w=16)
普通卷积：(输入通道10，输出通道为20，大小为5，padding为2，步长为3)
转置卷积：(输入通道为20，输出通道为ie10，大小为5，padding为2，步长为3)

代码实现：

X = torch.rand(size=(1, 10, 16, 16))
conv = nn.Conv2d(10, 20, kernel_size=5, padding=2, stride=3)
tconv = nn.ConvTranspose2d(20, 10, kernel_size=5, padding=2, stride=3)
tconv(conv(X)).shape == X.shape

True