下面我们先直接用代数式来证明一下:
设
y
1
=
arcsin
x
,
y
2
=
arccos
x
,求
y
1
+
y
2
由于
x
=
sin
y
1
=
cos
y
2
,而
cos
y
2
=
sin
(
y
2
+
π
2
)
那么就得到
y
1
=
y
2
+
π
2
,即
y
1
−
y
2
=
π
2
但我们说这样不成立,为什么?
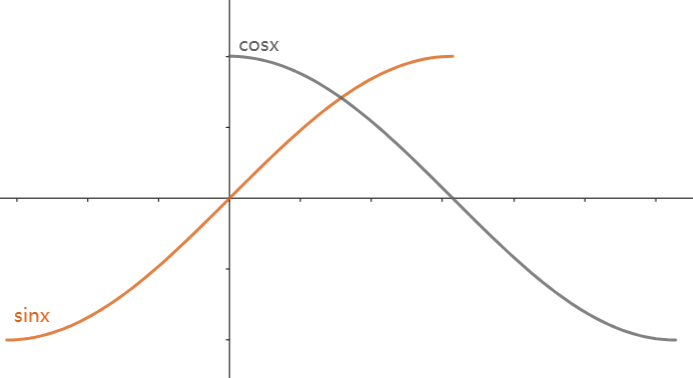
为了弄清原因,我们结合反三角函数的定义域、值域和图像来进行分析
如下图所示。
实际上
arcsin
x
只取
sin
x
在
[
−
π
2
,
π
2
]
的那一段图像做关于
y
=
x
的对称
而
arccos
x
只取
cos
x
在
[
0
,
π
]
的那一段图像做关于
y
=
x
的对称
因此在上述推导过程中,
y
1
的范围是
[
−
π
2
,
π
2
]
,
y
2
的范围是
[
0
,
π
]
sin
(
y
2
+
π
2
)
的范围是
[
π
2
,
3
π
2
]
不属于
[
−
π
2
,
π
2
]
的范围
因此
sin
(
y
2
+
π
2
)
不成立
那如何推出正确的结论呢?
由于
cos
x
是偶函数,因此
cos
y
2
=
cos
(
−
y
2
)
=
sin
(
−
y
2
+
π
2
)
sin
(
−
y
2
+
π
2
)
的范围是
[
−
π
2
,
π
2
]
,因此成立
最终有
x
=
sin
y
1
=
cos
y
2
=
cos
(
−
y
2
)
=
sin
(
−
y
2
+
π
2
)
因此
y
1
=
−
y
2
+
π
2
,即
y
1
+
y
2
=
π
2
即
arcsin
x
+
arccos
x
≡
π
2
下面我们先直接用代数式来证明一下: \\ 设y_1=\arcsin x,y_2=\arccos x,求y_1+y_2 \\ 由于x=\sin y_1=\cos y_2,而\cos y_2=\sin(y_2+\frac{\pi}{2}) \\ 那么就得到y_1=y_2+\frac{\pi}{2},即y_1-y_2=\frac{\pi}{2} \\ 但我们说这样不成立,为什么?\\ \,\\ 为了弄清原因,我们结合反三角函数的定义域、值域和图像来进行分析 \\ 如下图所示。\\ 实际上\arcsin x只取\sin x在[-\frac{\pi}{2},\frac{\pi}{2}]的那一段图像做关于y=x的对称 \\ 而\arccos x只取\cos x在[0,\pi]的那一段图像做关于y=x的对称 \\ 因此在上述推导过程中,y_1的范围是[-\frac{\pi}{2},\frac{\pi}{2}],y_2的范围是[0,\pi] \\ \,\\ \sin(y_2+\frac{\pi}{2})的范围是[\frac{\pi}{2},\frac{3\pi}{2}]不属于[-\frac{\pi}{2},\frac{\pi}{2}]的范围 \\ 因此\sin(y_2+\frac{\pi}{2})不成立 \\ \,\\ 那如何推出正确的结论呢?\\ 由于\cos x是偶函数,因此\cos y_2=\cos(-y_2)=\sin(-y_2+\frac{\pi}{2}) \\ \sin(-y_2+\frac{\pi}{2})的范围是[-\frac{\pi}{2},\frac{\pi}{2}],因此成立 \\ 最终有x=\sin y_1=\cos y_2=\cos(-y_2)=\sin(-y_2+\frac{\pi}{2}) \\ 因此y_1=-y_2+\frac{\pi}{2},即y_1+y_2=\frac{\pi}{2} \\ 即\arcsin x+\arccos x\equiv\frac{\pi}{2}
下面我们先直接用代数式来证明一下:设y1=arcsinx,y2=arccosx,求y1+y2由于x=siny1=cosy2,而cosy2=sin(y2+2π)那么就得到y1=y2+2π,即y1−y2=2π但我们说这样不成立,为什么?为了弄清原因,我们结合反三角函数的定义域、值域和图像来进行分析如下图所示。实际上arcsinx只取sinx在[−2π,2π]的那一段图像做关于y=x的对称而arccosx只取cosx在[0,π]的那一段图像做关于y=x的对称因此在上述推导过程中,y1的范围是[−2π,2π],y2的范围是[0,π]sin(y2+2π)的范围是[2π,23π]不属于[−2π,2π]的范围因此sin(y2+2π)不成立那如何推出正确的结论呢?由于cosx是偶函数,因此cosy2=cos(−y2)=sin(−y2+2π)sin(−y2+2π)的范围是[−2π,2π],因此成立最终有x=siny1=cosy2=cos(−y2)=sin(−y2+2π)因此y1=−y2+2π,即y1+y2=2π即arcsinx+arccosx≡2π
证明arcsinx+arccosx=π/2,并且为什么arcsinx-arccosx=π/2不成立
news2026/2/12 15:27:15
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/942463.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
ViewPager+ Fragment结合的setUserVisibleHint()调用时机
最近的项目使用到了ViewPager Fragment的模式,要求在每次Fragment获取显示的时候来刷新数据,该项目下ViewPager有5个子fragment,在onCreateView及fragment的**setUserVisibleHint(bool isVisibleToUser)**中的isVisibleToUser为t…
Jmeter(二十七):BeanShell PostProcessor跨线程全局变量使用
在性能测试中,两个相关联的接口不一定都在同一个线程组,遇见这种情况时,我们要进行跨线程组传参,此处用登录和查询配送单两个请求举例;
1、登录请求中配置json提取器,将接口返回的token保存在变量中&#…
Linux 指令心法(二)`cd` 更改当前目录
文章目录 命令的概述和用途命令的用法命令行选项和参数的详细说明命令的示例命令的注意事项或提示 命令的概述和用途
cd 是 “Change Directory” 的缩写。这是一个 shell 内建命令,用于在 Linux 和 Unix 系统中改变当前工作目录。通过使用 cd 命令,用户…
Python小知识 - Python中的多线程
Python中的多线程 线程是进程中的一个执行单元,是轻量级的进程。一个进程可以创建多个线程,线程之间共享进程的资源,比如内存、文件句柄等。 在Python中,使用threading模块实现线程。 下面的代码创建了两个线程,一个输…
【数学建模】清风数模正课5 相关性分析
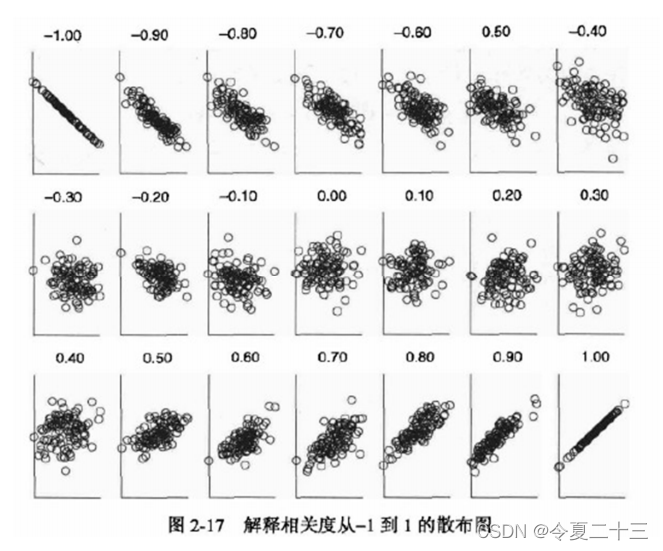
相关系数
相关性分析的关键是计算相关系数,在本节课中将会介绍两种常用的相关系数:皮尔逊相关系数(Pearson)和斯皮尔曼相关系数(Spearman)。
它们可以用来衡量两个变量间相关性的大小,对于不同…
后端面试话术集锦第三篇:spring cloud 面试话术
🚗后端面试集锦目录 💖后端面试话术集锦第一篇:spring面试话术💖 💖后端面试话术集锦第二篇:spring boot面试话术💖 💖后端面试话术集锦第三篇:spring cloud面试话术💖 💖后端面试话术集锦第四篇:ElasticSearch面试话术💖 💖后端面试话术集锦第五篇:r…
面试现场表现:展示你的编程能力和沟通技巧
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…
【力扣】55、跳跃游戏
var canJump function(nums){let cover 0;for(let i0;i<nums.length;i){if(i<cover){cover Math.max(nums[i]i,cover);if(cover >nums.length-1){return true;}}}}
春秋云镜 CVE-2018-7448
春秋云镜 CVE-2018-7448 CMS Made Simple 2.1.6 RCE
靶标介绍
CMS Made Simple 2.1.6版本存在代码注入漏洞,可以通过 timezone 参数执行任意代码。
启动场景 漏洞利用
1、目的文件夹选择/var/www/html/cms 2、next到第四步,数据库名:cms…
2023-8-29 有向图的拓扑排序
题目链接:有向图的拓扑排序
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N 100010;int n, m;
int h[N], e[N], ne[N], idx;int q[N], d[N];void add(int a, int b)
{e[idx] b, ne[idx] h[a]…
Android11.0 Launcher3定制化功能之抽屉式(双层)app列表排序功能实现
1.概述 在11.0的系统开发中,在定制Launcher3的开发中,对于抽屉式即双层桌面的workspace的app列表排序的功能,也是常有的需求,把常用的app图标放在前面,其他的可以放在列表后面做个整体的排序,这就需要了解app列表排序的流程,然后根据需求来实现功能
如图:
2.Launche…
面试中的代码写作:如何撰写清晰、高效的示例代码
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…
代码随想录算法训练营之JAVA|第四十二天|70. 爬楼梯
今天是第 天刷leetcode,立个flag,打卡60天,如果做不到,完成一件评论区点赞最高的挑战。
算法挑战链接 70. 爬楼梯https://leetcode.cn/problems/climbing-stairs/
第一想法
这是一个动态规划的入门题目,在看完完全背…
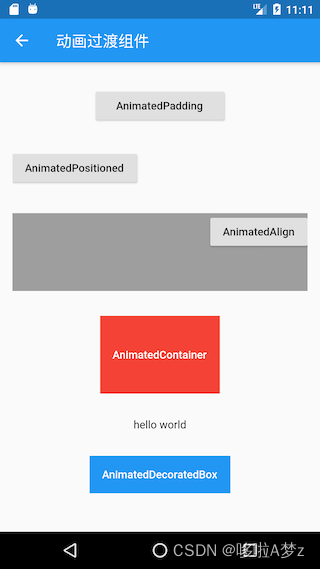
Flutter(九)Flutter动画和自定义组件
目录 1.动画简介2.动画实现和监听3. 自定义路由切换动画4. Hero动画5.交织动画6.动画切换7.Flutter预置的动画过渡组件自定义组件1.简介2.组合组件3.CustomPaint 和 RenderObject 1.动画简介
Animation、Curve、Controller、Tween这四个角色,它们一起配合来完成一个…
ros2官方文档(基于humble版本)学习笔记
ros2官方文档(基于humble版本)学习笔记(一) 一、安装ROS2二、按教程学习1.CLI 工具配置环境 由于市面上专门讲ROS2开发的书籍不多,近期看完了《ROS机器人开发实践》其中大部分内容还是基于ROS1写的,涉及top…
【Linux】深入理解文件缓冲区
文章目录 问题引入如何理解缓冲区缓冲区刷新策略问题解释模拟一个文件缓冲区 问题引入
首先看一段代码:
#include <stdio.h>
#include <string.h>
int main()
{const char *msg0"hello printf\n";const char *msg1"hello fwrite\n&quo…
Ae 效果:CC Image Wipe
过渡/CC Image Wipe Transition/CC Image Wipe CC Image Wipe(CC 图像擦除)效果的主要用途是通过使用图像的某个属性(如红通道、绿通道、蓝通道、Alpha 通道、亮度、明度、色相或饱和度)来创建一个独特的过渡效果,可以…
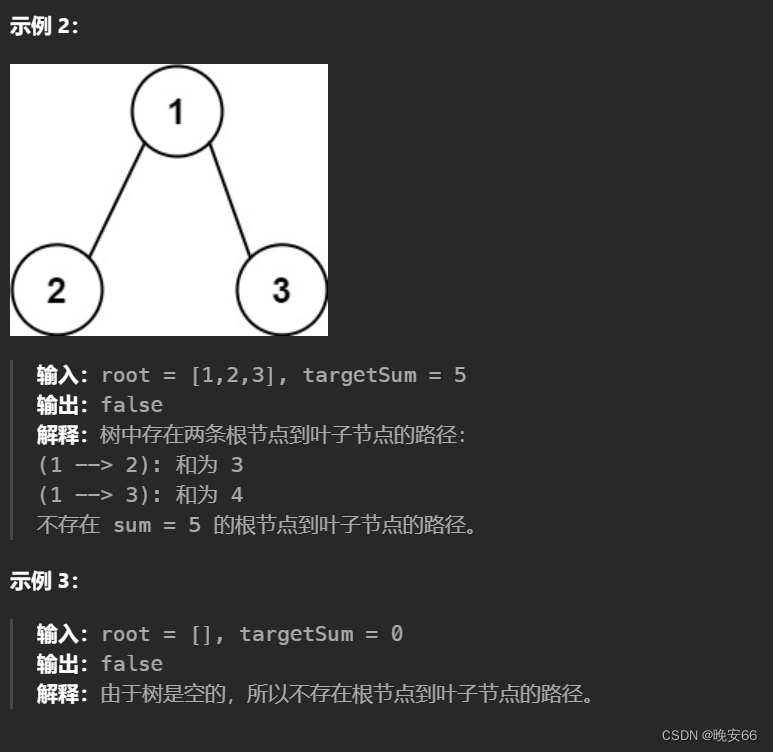
【算法与数据结构】112、LeetCode路径总和
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:本题通过计算根节点到叶子节点路径上节点的值之和,然后再对比目标值。利用文章【算法和数据…