相关系数
相关性分析的关键是计算相关系数,在本节课中将会介绍两种常用的相关系数:皮尔逊相关系数(Pearson)和斯皮尔曼相关系数(Spearman)。
它们可以用来衡量两个变量间相关性的大小,对于不同类型的数据,我们要用不同的相关系数进行计算分析。
统计学概念
在学习这两个系数之前,我们需要了解一些必要的概率统计中的概念,以便于公式的理解和推导。
| 总体 | 所要考察对象的全部个体 |
| 样本 | 从总体中抽取的一部分个体 |
为了对考察对象进行分析,我们总是希望得到总体数据的一些特征,例如均值、方差、标准差等;
但总体数据往往过多,以致于难以进行计算,因此我们可以计算从从总体中抽取的样本的统计量,以此来估计总体的统计量。
皮尔逊相关系数
总体皮尔逊相关系数

X和Y的变化方向相同:当X大于其均值时,Y也大于其均值,当X小于其均值时,Y也小于其均值
协方差的本质:若X和Y的变化方向相同,则协方差为正;若X和Y的变化方向相反,则协方差为负;若X和Y的变化方向无关联,则协方差正负抵消为零。
注意:协方差的大小和两个变量的量纲有关,因此不适合做比较。
皮尔逊相关系数的本质:可以看作剔除了两个变量量纲影响、将X和Y标准化后的协方差。
样本皮尔逊相关系数

相关系数可视化
在计算相关系数之前,需要通过绘制散点图来判断X和Y之间的相关性,如果散点图显示二者不相关,那么计算出的相关系数也就没有意义了。
只有先确定两个变量是线性相关的,相关系数才能告诉我们这两个变量的相关程度如何。
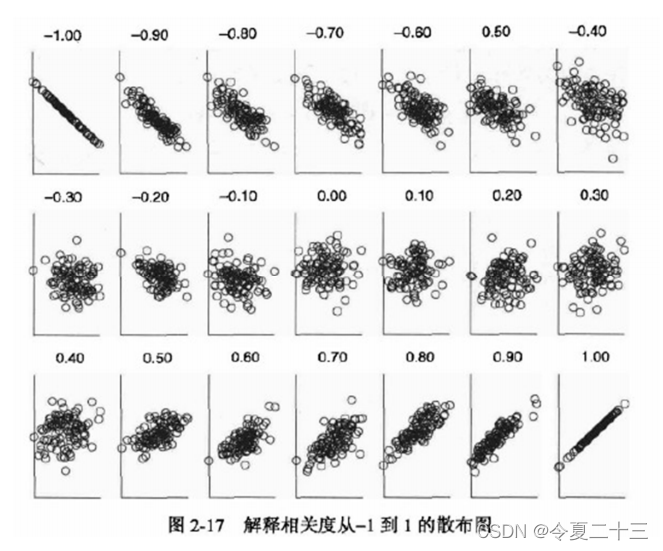
事实上,比起相关系数的大小,我们往往更关注的是其显著性,这就需要进行假设检验。