1、先序遍历

先序遍历使用了栈的结构，先压入根节点，然后依次将其右子节点和左字节点压入。然后就可以实现“头左右”的遍历顺序

/**
     * 先序遍历
     */
    public static void pre_order(TreeNode treeNode){
        if (treeNode == null){
            return;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.add(treeNode);
        while(!stack.isEmpty()){
            TreeNode poll = stack.pop();
            //处理数据
            System.out.println(poll.val);

            if (poll.right != null){
                stack.add(poll.right);
            }
            if (poll.left != null){
                stack.add(poll.left);
            }
        }

    }

2、中序遍历

中序遍历是三种遍历顺序中较难理解的一个，也是利用了一个栈的结构，先一次性将根节点的所有沿着左孩子压入栈中，到底后取出，此时进行数据处理。判断取出来的节点有没有右孩子，有的话就将这个节点的右孩子看成新的节点，继续将其左孩子压入栈中，这样操作直至栈空。

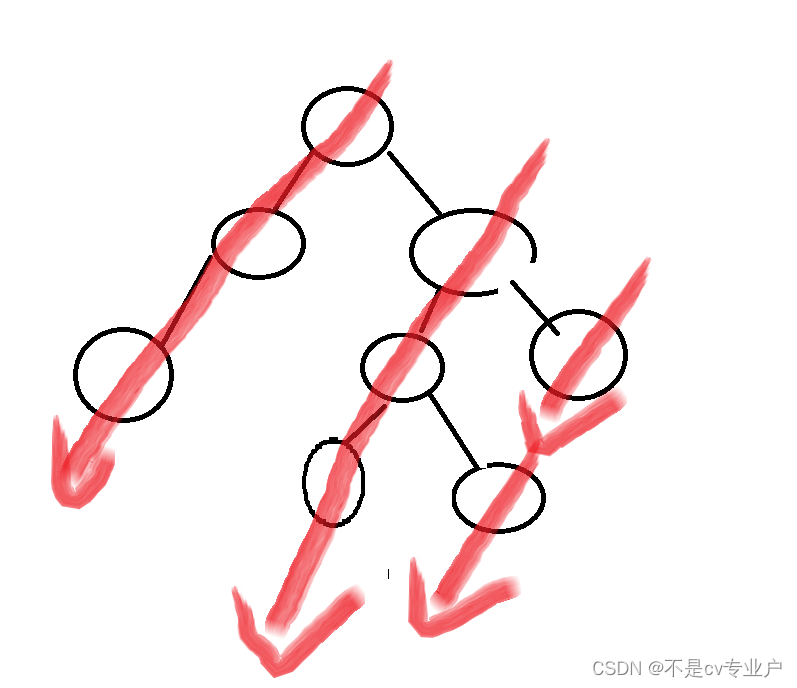不太理解下面代码的可以借助这张图来理解，压入栈的顺序是按箭头位置，先左边，再右边，然后因为是从头到底压入栈，所以孩子会先出栈，先被遍历到，然后才是它的父亲节点，所以形成了 “左头右”。

 /**
     * 中序遍历
     */
    public static void middle_order(TreeNode treeNode){
        if (treeNode == null){
            return;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.add(treeNode);
        while(!stack.isEmpty()){
            if (treeNode.left!=null){
                stack.add(treeNode.left);
                treeNode = treeNode.left;
            }else {
                TreeNode pop = stack.pop();
                //处理数据
                System.out.println(pop.val);
                if (pop.right != null){
                    stack.add(pop.right);
                    treeNode = pop.right;
                }
            }
        }
    }

3、后序遍历

这个遍历就是用两个栈，先使用类似先序遍历，然后就再将弹出的节点，再次压入新的栈中，就将原来的 “头右左” 变为了 “左右头”。

/**
     * 后序遍历
     */
    public static void post_order(TreeNode treeNode){
        if (treeNode == null){
            return;
        }
        Stack<TreeNode> stackLeft = new Stack<>();
        Stack<TreeNode> stackRight = new Stack<>();
        stackLeft.add(treeNode);
        while(!stackLeft.isEmpty()){
            TreeNode pop = stackLeft.pop();
            if (pop.left != null){
                stackLeft.add(pop.left);
            }
            if ((pop.right != null)){
                stackLeft.add((pop.right));
            }
            stackRight.add(pop);
        }
        while (!stackRight.isEmpty()){
            //处理数据，此时这个栈中数据就是后序排列
            System.out.println(stackRight.pop().val);
        }
    }