1005.K次取反后最大化的数组和
思路一:求出正负数的个数,根据k值来进行取反
134.加油站
思路:考虑总油量和当前剩余油量,同时遍历两个数组,当前剩余油量小于0时,说明在 i 之前都无法出发。
135.分发糖果
思路:考虑左右两个维度,并且在考虑第二个维度的时候,需要取上一个维度和当前维度的最大值,而不是盲目添加
452.用最少数量的箭引爆气球
思路:先按照左边界进行排序,再遍历数组
-
1.判断第 i 个位置的气球和第 i-1 个位置的气球是否重合,不重合的话需要箭+1;
-
2.重合的话,需要更新右边界,因为下一个气球需要跟前两个气球都重合
class Solution {
public:
int findMinArrowShots(vector<vector<int>>& points) {
int n=points.size();
if(n==0) return 0;
int res=1;
sort(points.begin(),points.end());
int end=points[0][1];
for(int i=1;i<n;i++){//相邻两两比较
if(points[i][0]>points[i-1][1])//不重合时,需要增加箭
res++;
else//重合时,需要更新重合右边界
points[i][1]=min(points[i-1][1],points[i][1]);
}
return res;
}
};435.无重叠区间
思路:计算出重叠区间个数
-
1.排序
-
2.当第 i 个区间和第 i-1 个区间重叠时,个数+1,因为第 i 个区间相当于要删掉,所以更新第 i 个区间的右边界为第 i-1 个区间的右边界和第 i 个区间的右边界的较小值。
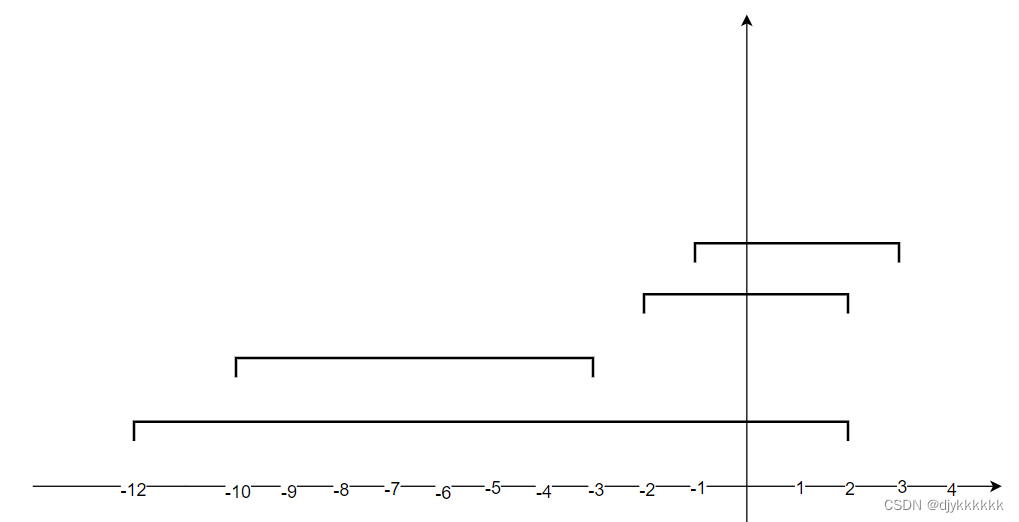
为什么重叠时,当前区间的右边界要更新为较小值呢?因为我们要求最少删除的重叠区间,就是求最大的不重叠区间,排序后,当两个区间重叠时,我们要选择较早结束的那个区间留下来,因为要避免和后面的区间重叠!!!
763.划分字母区间
思路:获取每个字母的最远出现长度,然后第二次遍历数组,使用两个变量维护一个重复区间,
右边界被遍历到之前一直处于更新状态;
当右边界被遍历到时,说明区间内的字母接下来都不会出现了(因为记的是最远出现距离),此时记录边界长度,并且把下一个区间的左边界更新到 i+1;
class Solution {
public:
vector<int> partitionLabels(string s) {
int hash[27]={0};
for(int i=0;i<s.size();i++)//记录字母在字符串中出现的最远位置
hash[s[i]-'a']=i;
vector<int>res;
int left=0,right=0;
for(int i=0;i<s.size();i++){
right=max(right,hash[s[i]-'a']);//记录这一段区间内最大长度
if(i==right){//当遍历到最远位置时
res.push_back(right-left+1);//获取当前区间的长度
left=i+1;//把左边界放到后面
}
}
return res;
}
};56.合并区间
思路一:先排序,然后根据右边界进行判断;重叠和不重叠的情况(相比较之前的题轻松一些)
class Solution {
public:
// static bool cmp(const vector<int>&a,const vector<int>&b){
// return a[0]<b[0];
// }
vector<vector<int>> merge(vector<vector<int>>& intervals) {
int n=intervals.size();
sort(intervals.begin(),intervals.end());
vector<vector<int>>res;
vector<int>mid;
mid=intervals[0];
for(int i=1;i<n;i++){
cout<<intervals[i][0]<<endl;
if(intervals[i][0]<=intervals[i-1][1]){//重合时,更新mid最大边界,
//并且更新当前区间最大边界
mid[1]=max(intervals[i][1],intervals[i-1][1]);
intervals[i][1]=mid[1];
}
else{//不重叠时,添加mid并且更新mid为当前数组
res.push_back(mid);
mid.clear();
mid=intervals[i];
}
}
if(!mid.empty()) res.push_back(mid); //还有结束没添加的情况
return res;
}
};738.单调递增的数字
思路:从后向前遍历,找到前一位比当前位大的数,把前一位减1,然后记录当前位置
二次遍历,把当前位置以后的位置全部编程最大值9
class Solution {
public:
int monotoneIncreasingDigits(int n) {
string mid=to_string(n);
int flag=mid.size();
for(int i=mid.size()-1;i>0;i--){
if(mid[i]<mid[i-1]){
flag=i;//记录改变位置的后一位
mid[i-1]--;//前一位减1
}
}
for(int i=flag;i<mid.size();i++)
mid[i]='9';//从改变位置后面依次改成9
return stoi(mid);
}
};