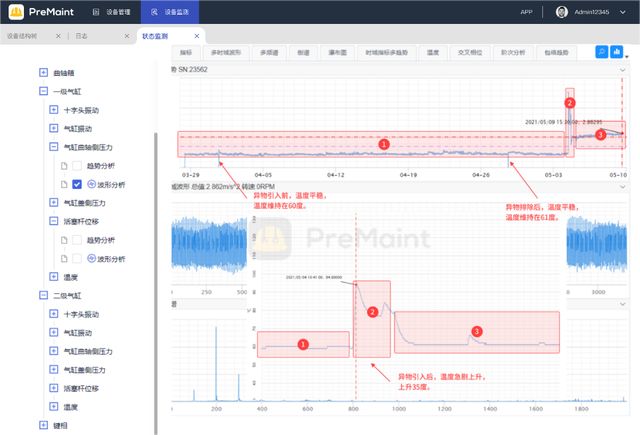
题目描述

贪心策略
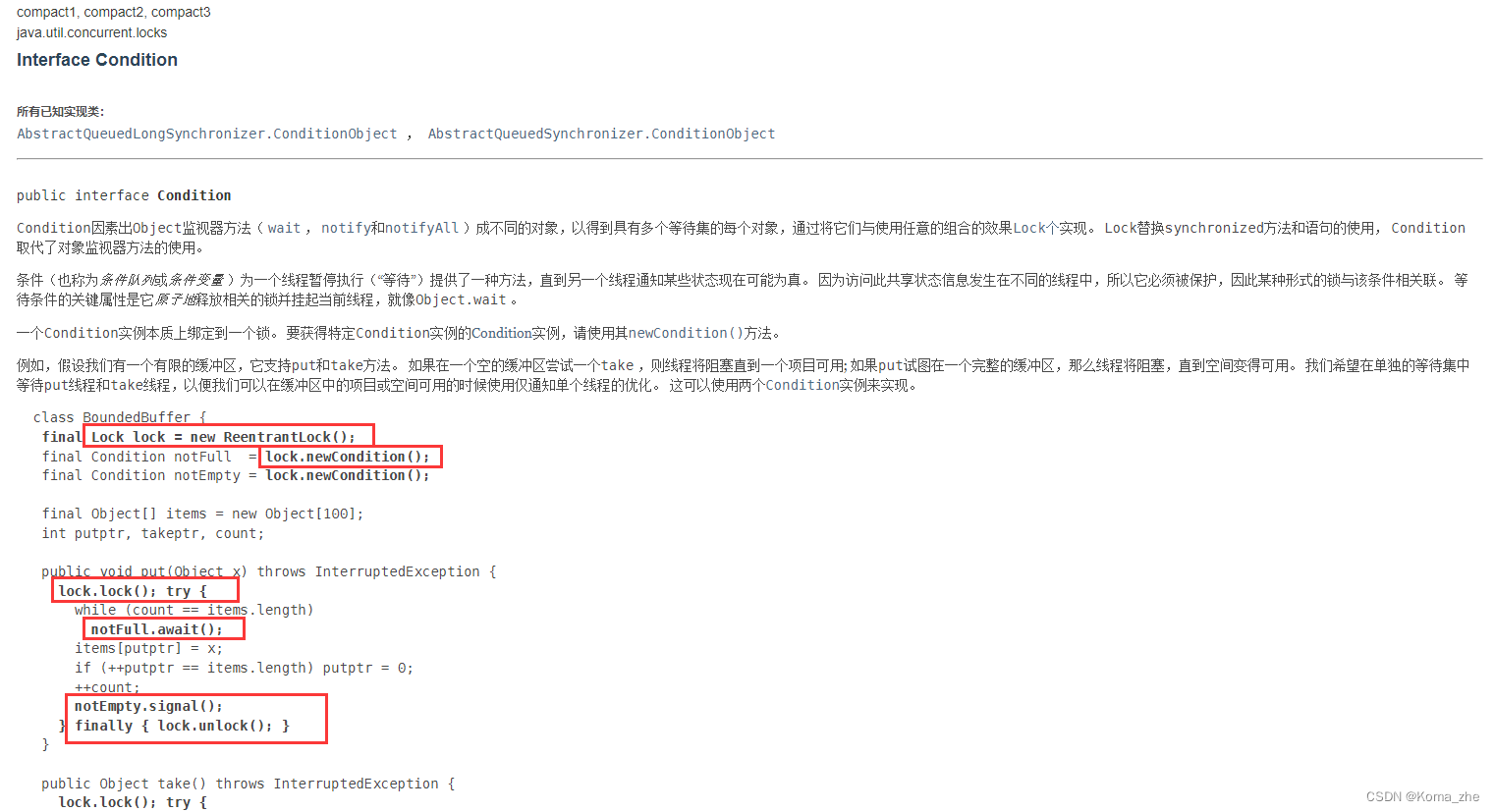
首先按右端点对区间进行排序
然后从左到右遍历每一个区间,如果这个区间还没有选中的点,那么就选择这个区间的右端点,否则就pass掉这个区间
举一个栗子

贪心策略证明
假设最少的选点数为:ans
利用上述贪心策略得到的最终选点数为:cnt
现在核心是证明:ans=cnt
只需要证明:
1.ans<=cnt
2.ans>=cnt
证明方式如下:
1.ans的定义就是最少的选点数,所以肯定ans<=cnt
2.首先让我们再读一遍贪心策略的要求:“如果这个区间还没有选中的点,那么就选择这个区间的右端点,否则就pass掉这个区间”,什么时候选中右端点呢?就是遍历到某一个区间的时候,还没有选到这个区间上的任意一个点:
举一个例子,现在有三个已经排好序的区间,(1,2)(3,4)(5,6),遍历第一个区间(1,2)的时候,肯定还没有选点,所以要选中坐标为2的点,当遍历到第二个区间(3,4)时,要选中坐标为4的点,为什么此时要选一个新的点4呢?核心原因是(1,2)和(3,4)这两个区间没有交集,所以一直执行下去的话,最终就会得到一个贪心解cnt(含义和上面的定义完全一样),也就意味着,我们找到了cnt个两两没有交集的区间,当然总区间数肯定是大于等于cnt的,因为有的区间肯定会发生相交。
根据上述的分析,现在我们就知道一个事实:
如果说用这种贪心策略去处理一些区间集合,并且最终输出cnt,那么就一定说明在这个区间集合中可以找到cnt个两两不相交的区间。
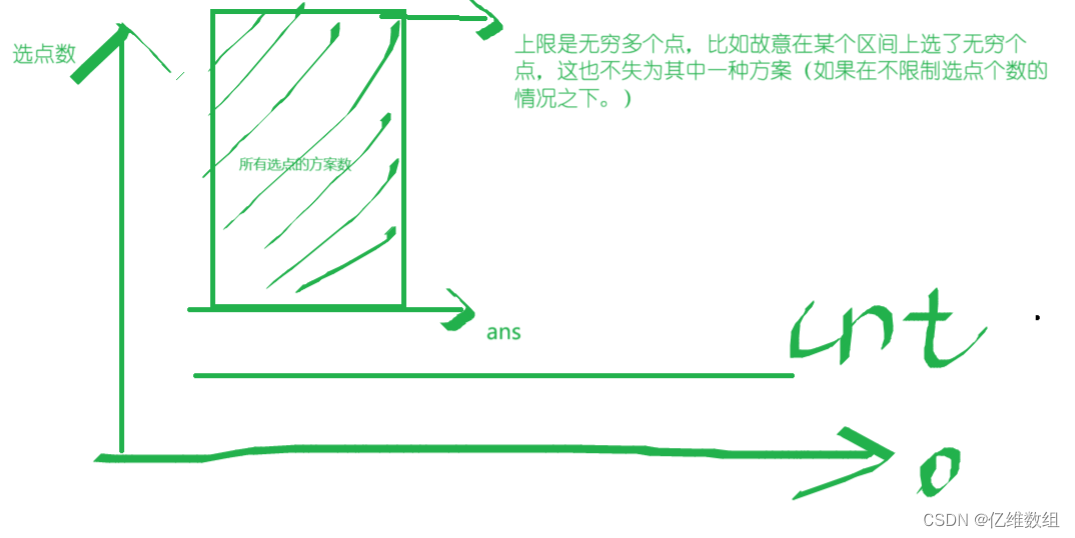
然后抛开贪心策略,眼光仅仅盯在这cnt个区间上,显而易见,此时我们选点的话,肯定最少要选cnt个点,至于用不用选其它更多的点,我们不用管,因为这样我们已经得到了一个事实了,即:所有选点的方案的点数必然是大于等于cnt的,如下图:至于ans和cnt的关系不用纠结是不是一定相等了,反正大于等于的情况是包含相等的。
代码
#include<iostream>
#include<algorithm>
using namespace std;
const int N=100010;
int n;
struct Range{
int l,r;
}range[N];
bool cmp(struct Range a,struct Range b)
{
return a.r<b.r;
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
{
cin>>range[i].l>>range[i].r;
}
sort(range,range+n,cmp);
int res=0,ed=-2e9;
for(int i=0;i<n;i++)
if(ed<range[i].l)
ed=range[i].r,res++;
cout<<res;
return 0;
}