目录

题目：

示例：

分析：

代码：

---

题目：

示例：

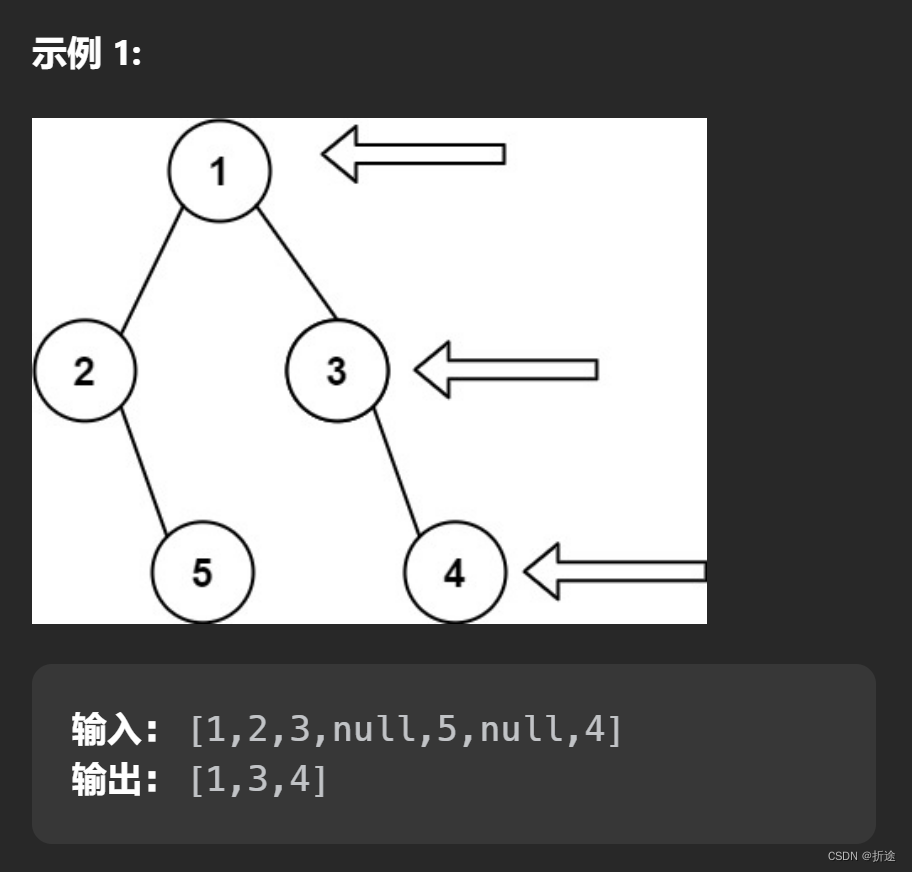
分析：

题目给我们一棵二叉树，让我们返回站在二叉树右边从上到下看到的节点。

那实际上就是要我们对二叉树进行层序遍历，然后把每层的最右边的一个节点拿出来。

所以问题实际上就是要我们对二叉树进行层序遍历，所以我们这边介绍两种层序遍历的方法，分别是DFS和BFS，也就是深度优先搜索和广度优先搜索。

首先是DFS深度优先搜索，我们先定义一个空的二维数组，是用来存放层序遍历的结果的。

我们对二叉树进行先序遍历，在递归遍历的同时携带一个代表深度的参数。

如果存放结果的二维数组的size也就是里面一维数组的数量小于等于深度，那就是我们第一次碰到这一层的节点，我们就往二维数组的后面塞一个一维的空数组。

然后再根据深度来将当前节点的值塞到二维数组的某个一维数组里。

先序遍历完毕，我们也就层序遍历完毕了。

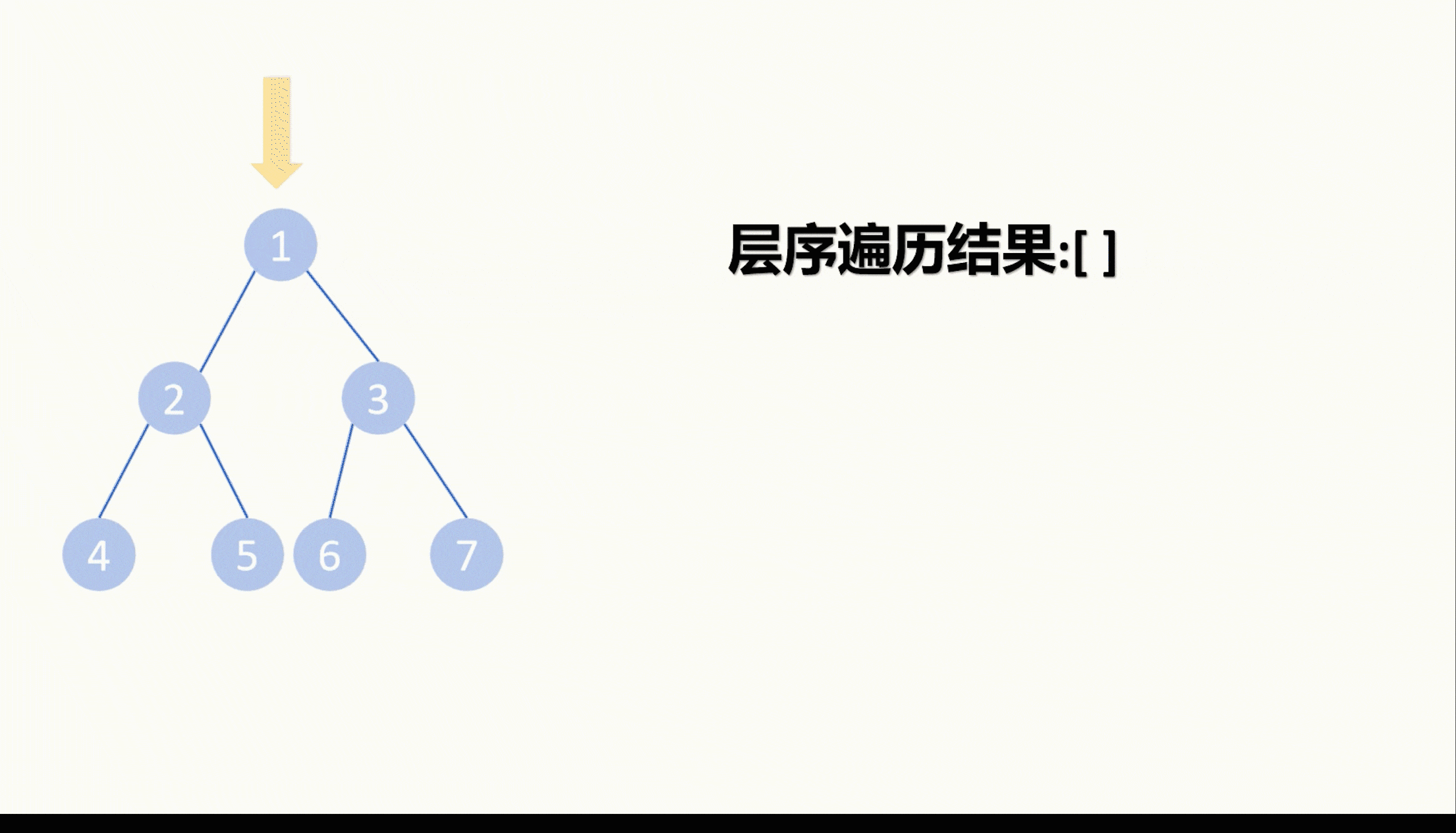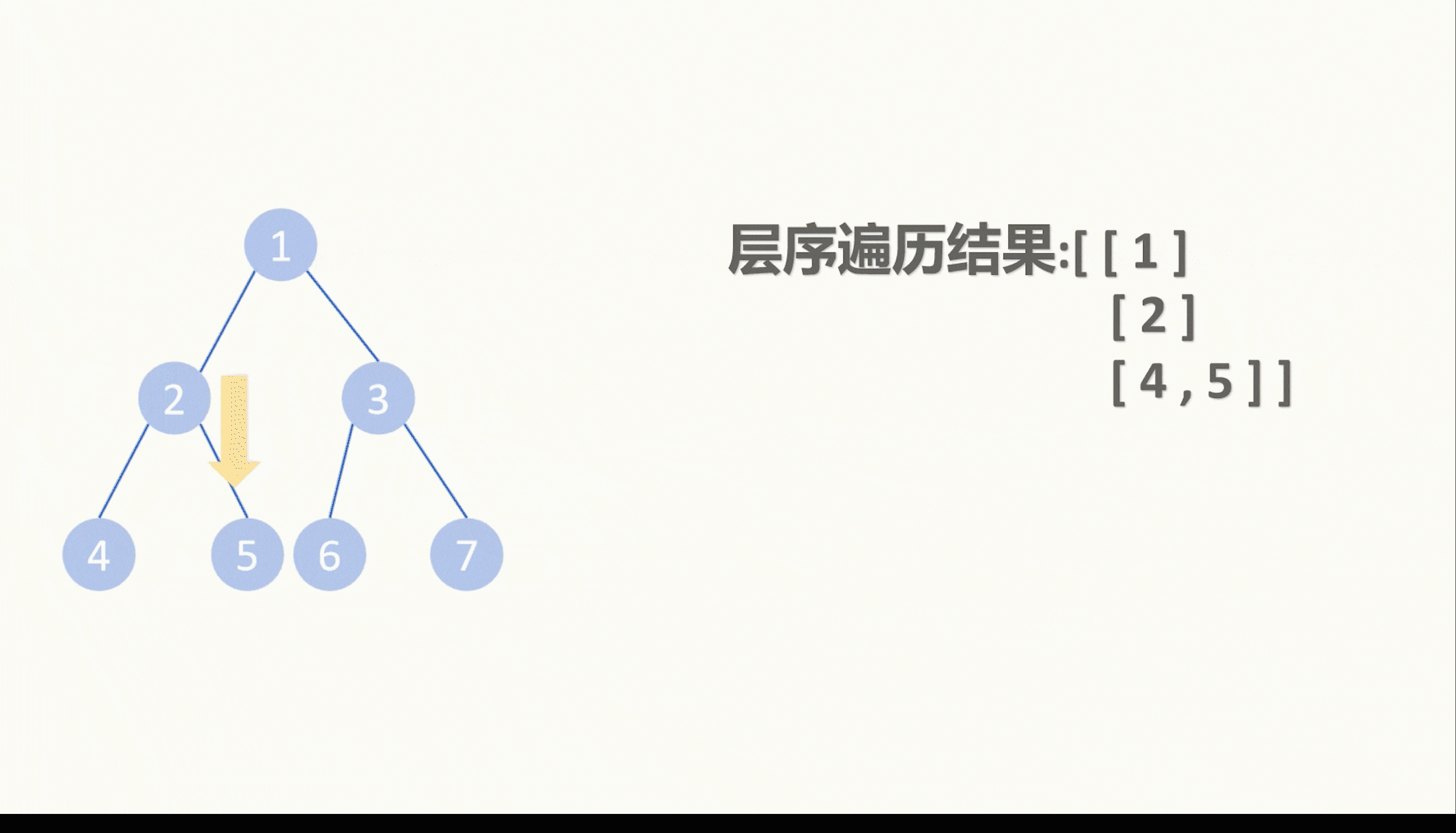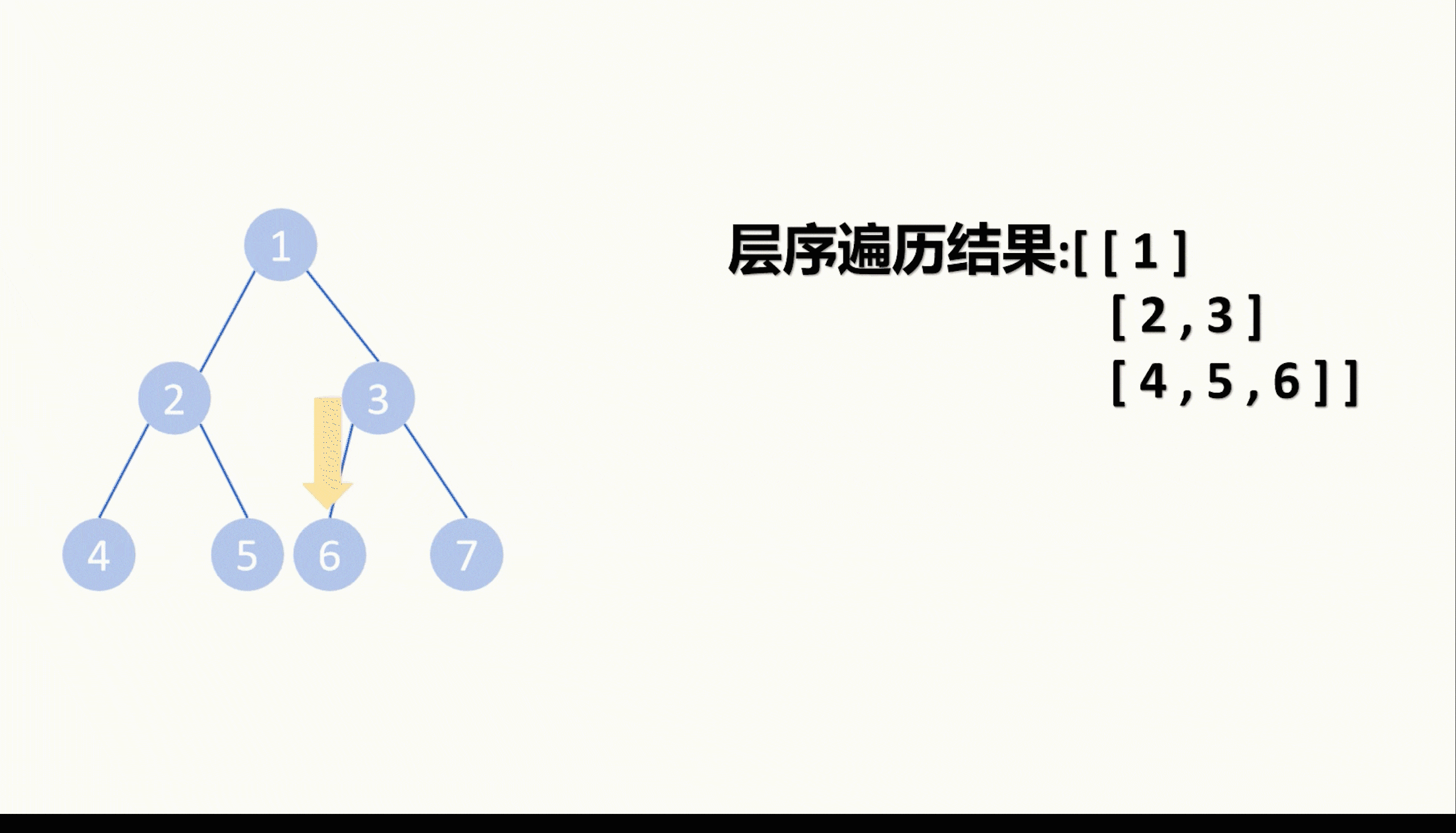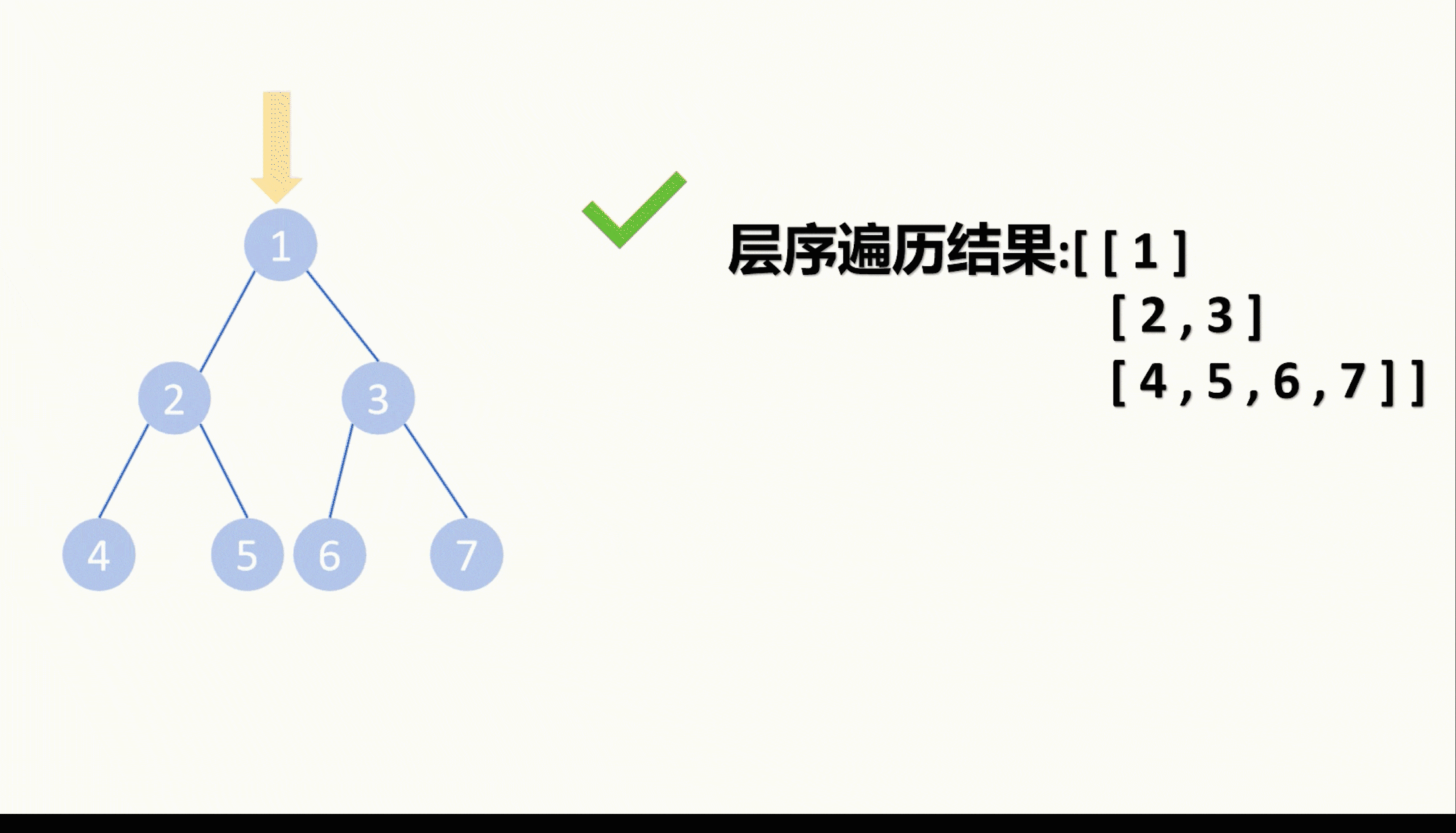
这是DFS层序遍历的方法。我个人认为比较简单，不过层序遍历最经典的是BFS广度优先搜索，所以这边我们也将一下BFS怎么层序遍历。

我们拿一个队列，首先先把跟节点塞进队列里。

然后进入一个while循环，只要队列为空我们就退出循环，在循环体里我们先给存层序遍历的二维列表里塞一个空的一维列表，然后先记录一下队列的长度，然后再for循环队列长度次数，在for循环里再每次取出一个队列里的节点，把节点的值塞进二维数组的最后一个一维数组里面。

再对节点做判断，如果其左子树不为空，就把左子节点塞进队列里，如果其右子树不为空，把右子节点再塞进去。

这样就是每次我们只取二叉树的一层节点，并且存住每层的节点值后，还把每个节点的子节点塞进了队列，这样队列里就是下一层的节点了。

直到队列为空，那么就表示层序遍历完毕。

最终二维数组就是我们层序遍历的结果。

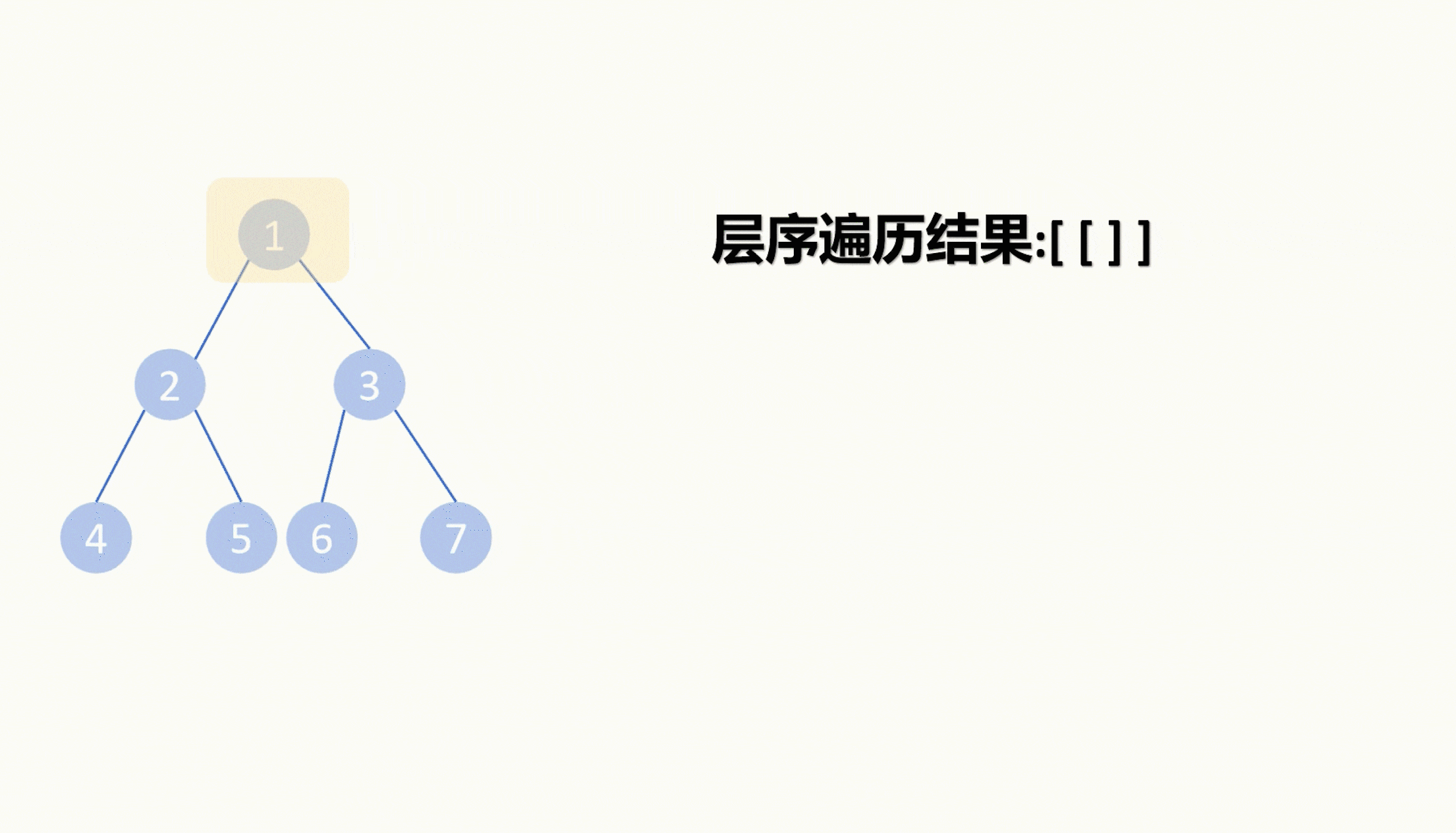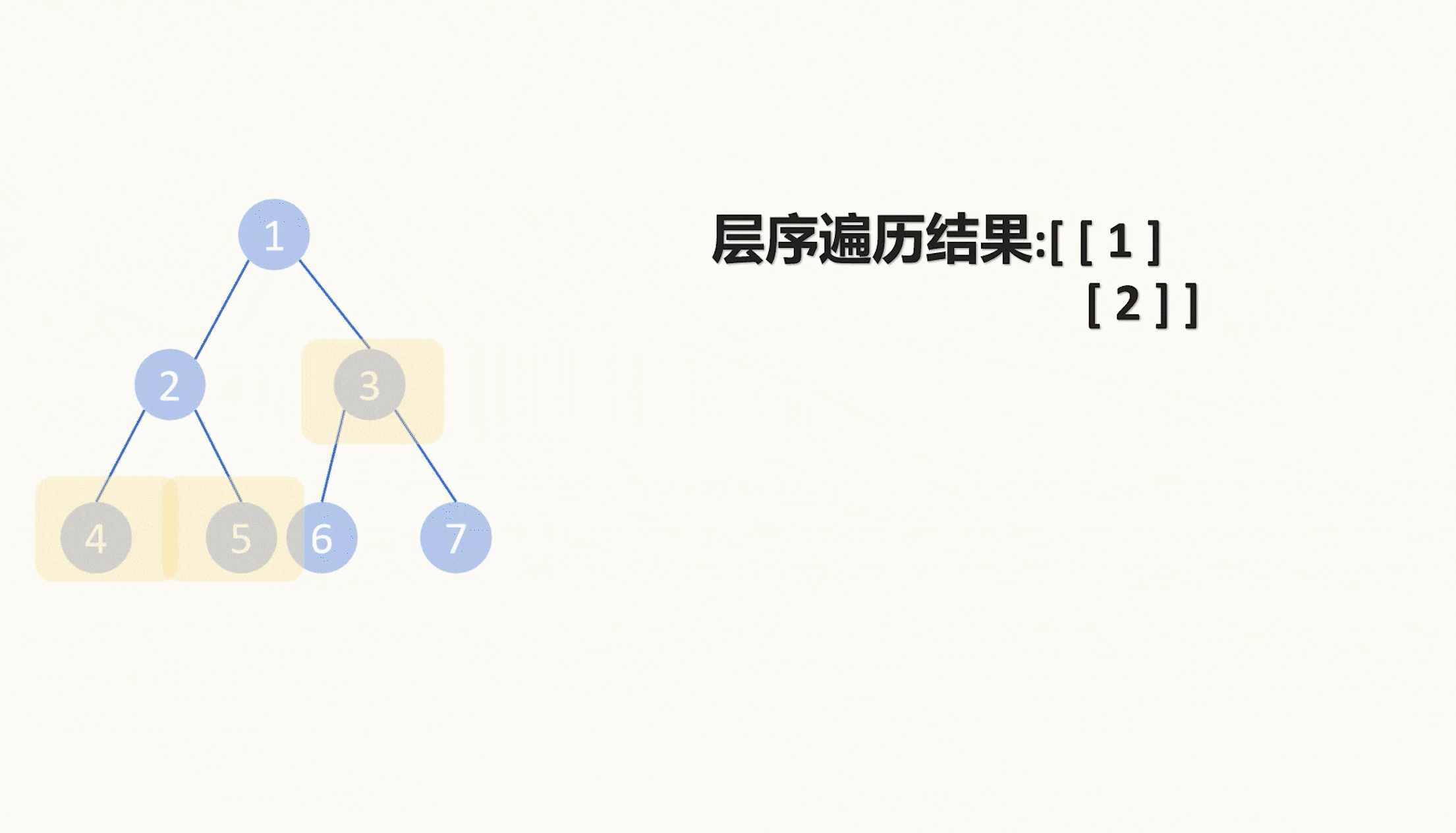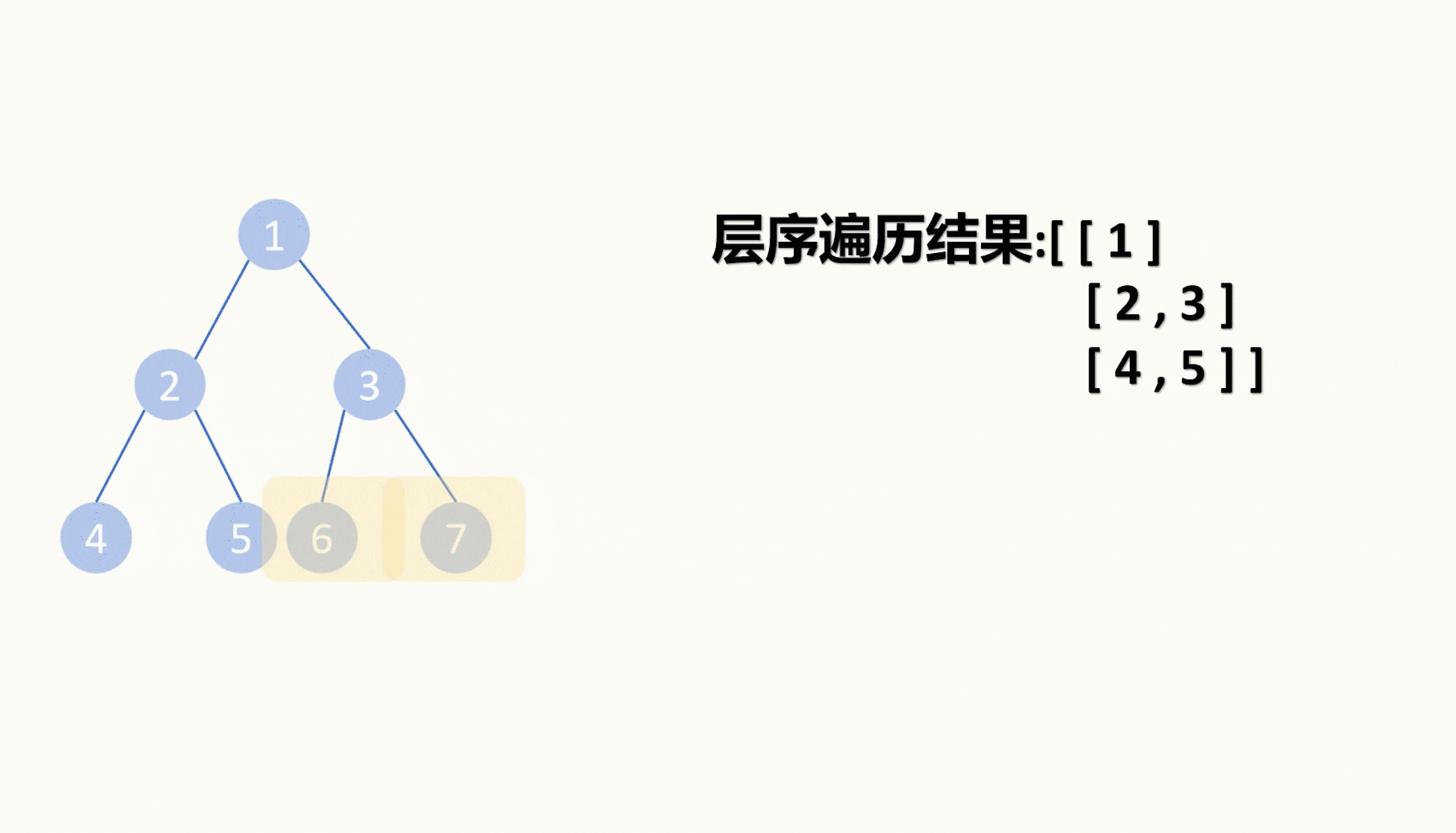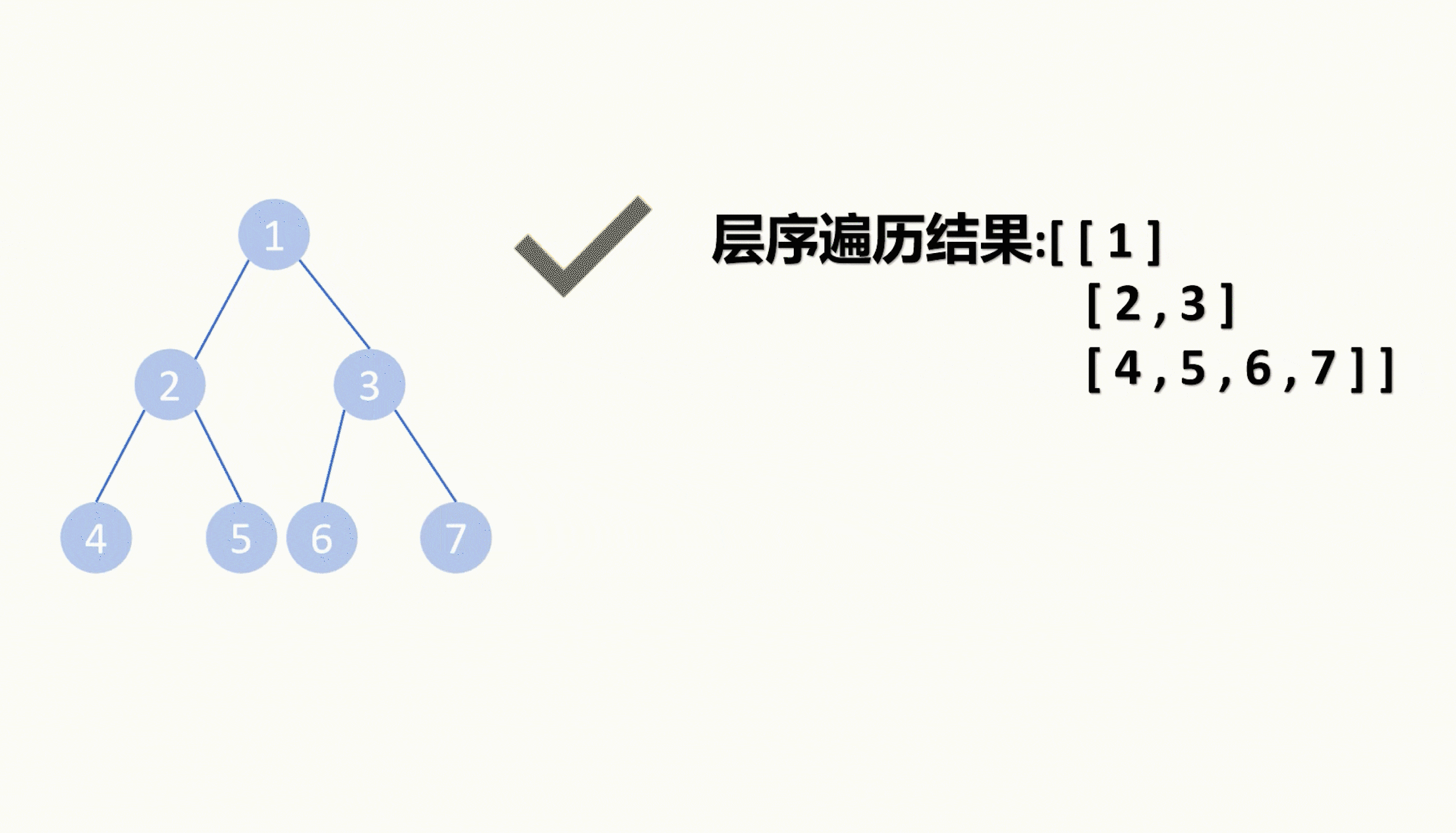
以上两种方法都可以对二叉树进行层序遍历。而本题中，我们需要把每层的最右边的节点返回出去，所以我们还需要取走二维数组里每个数组的最后一个元素。

代码：

DFS层序遍历

class Solution {
public:
    vector<vector<int>>cache;
    void find(TreeNode* root,int deep){
        if(root==nullptr) return;
        if(cache.size()<=deep) cache.push_back(vector<int>(0));
        cache[deep].push_back(root->val);
        find(root->left,deep+1);
        find(root->right,deep+1);
    }
    vector<int> rightSideView(TreeNode* root) {
        find(root,0);
        vector<int>res;
        for(auto&c:cache){
            res.push_back(*(c.end()-1));
        }
        return res;
    }
};

BFS层序遍历 

class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        if(root==nullptr) return {};
        vector<vector<int>>cache;
        queue<TreeNode*>q;
        q.push(root);
        while(!q.empty()){
            cache.push_back(vector<int>(0));
            int l=q.size();
            for(int i=0;i<l;i++){
                TreeNode* node=q.front();q.pop();
                cache.back().push_back(node->val);
                if(node->left) q.push(node->left);
                if(node->right) q.push(node->right);
            }
        }
        vector<int>res;
        for(auto& c:cache){
            res.push_back(*(c.end()-1));
        }
        return res;
    }
};