计算机毕设基于机器学习的餐厅销量预测 -大数据 python

news2024/12/29 10:32:56

文章目录

0 前言
餐厅销量预测
模型简介
- 2.ARIMA模型介绍
- - 2.1自回归模型AR
  - 2.2移动平均模型MA
  - 2.3自回归移动平均模型ARMA
三、模型识别
四、模型检验
- 4.1半稳性检验
- - (1)用途
  - (1)什么是平稳序列?
  - (2)检验平稳性
- ◆白噪声检验(纯随机性检验)
- - (1)用途
  - (1)什么是纯随机序列?
  - (2)检验纯随机性
五、Python实战
- （一）导入工具及数据
- （二）原始序列的检验
- （三）一阶差分序列的检验
- （四）定阶（参数调优）
- （五）建模与预测
最后

0 前言

🔥 这两年开始毕业设计和毕业答辩的要求和难度不断提升，传统的毕设题目缺少创新和亮点，往往达不到毕业答辩的要求，这两年不断有学弟学妹告诉学长自己做的项目系统达不到老师的要求。

为了大家能够顺利以及最少的精力通过毕设，学长分享优质毕业设计项目，今天要分享的是

🚩 **基于机器学习的餐厅销量预测 **

🥇学长这里给一个题目综合评分(每项满分5分)

难度系数：3分
工作量：3分
创新点：3分

餐厅销量预测

模型简介

2.ARIMA模型介绍

2.1自回归模型AR

自回归模型描述当前值与历史值之间的关系，用变量自身的历史时间数据对自身进行预测。自回归模型必须满足平稳性的要求。

自回归模型首先需要确定一个阶数p，表示用几期的历史值来预测当前值。p阶自回归模型的公式定义为：
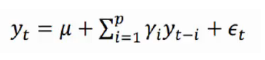
在这里插入图片描述

上式中yt是当前值,u是常数项,p是阶数
ri是自相关系数,et是误差。

自回归模型有很多的限制：
1、自回归模型是用自身的数据进行预测
2、时间序列数据必须具有平稳性
3、自回归只适用于预测与自身前期相关的现象

2.2移动平均模型MA

移动平均模型关注的是自回归模型中的误差项的累加，移动平均法能有效地消除预测中的随机波动，q阶自回归过程的公式定义如下：
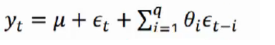
在这里插入图片描述

2.3自回归移动平均模型ARMA

自回归模型AR和移动平均模型MA模型相结合，我们就得到了自回归移动平均模型ARMA(p,q)，计算公式如下：
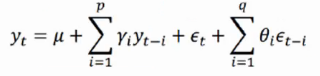
在这里插入图片描述

三、模型识别

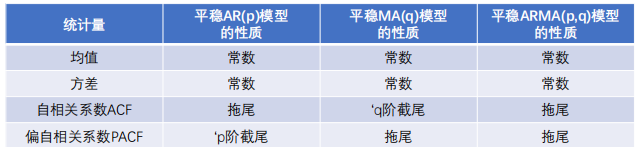
在这里插入图片描述
自相关函数ACF：时间序列观测值与其过去的观测值之间的线性相关性。

偏自相关函数PACF：在给定中间观测值的条件下，时间序列观测值预期过去的观测值之间的线性相关性

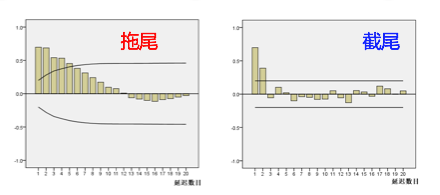
拖尾和截尾
拖尾指序列以指数率单调递减或震荡衰减，而截尾指序列从某个时点变得非常小：
在这里插入图片描述

四、模型检验

4.1半稳性检验

(1)用途

建模之前，检验时间序列数据是否满足平稳性，才能进-步建模

(1)什么是平稳序列?

如果时间序列在某-常数附件波动且波动范围有限，数学表达即常数均值和常数方差，并且延迟k期的序列变量的自协方差和自相关系数是相等的，则称该序列为平稳序列。

(2)检验平稳性

方法一:图检验(偏主观)
时序图检验:在某-常数附近波动且波动范围有限。
自相关图检验:平稳序列具有短期相关性,但随着延迟期数k的增加，自相关系数会快速衰减趋向于零。
方法二:单位根检验
不存在单位根即是平稳序列。

◆白噪声检验(纯随机性检验)

(1)用途

建模之前，检验数据是否满足白噪声检验，非白噪声才能进一步建模。
建模后，检验残差是否满足白噪声检验，通过检验,建模才成立。

(1)什么是纯随机序列?

如果-个序例是纯随机序列，那么序列值之间没有任何关系，则自相关系数为零(理论)或接近于零(实际) .

(2)检验纯随机性

方法- -:图检验
自相关图检验:自相关系数为零或接近于零
QQ图检验:大部分点在直线上,则数据符合正态分布
方法二: D-W检验或L .B统计量检验

五、Python实战

（一）导入工具及数据

#导入数据
sale=pd.read_excel(“C://Python//分享资料2//arima_data.xls”)
print(sale.head())
print(sale.info())

查看数据
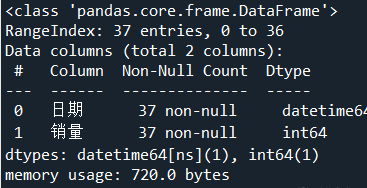
在这里插入图片描述

共有37个整数型样本数据

（二）原始序列的检验

#时序图观看是否平稳序列
plt.figure(figsize=(10,5))
sale[‘销量’].plot()
plt.legend([‘销量’])
plt.show()

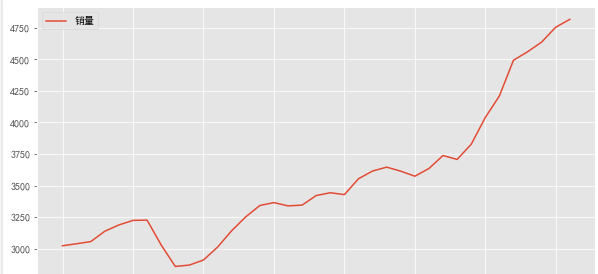
在这里插入图片描述

上图为一个单调递增的序列，说明数据是不平稳的。

自相关图

# 查看自相关图
sale[‘销量’]=sale[‘销量’].astype(‘float’)
plot_acf(sale[‘销量’],lags=35).show()
#解读：自相关系数长期大于零，没有趋向于零，说明序列间具有很强的长期相关性。

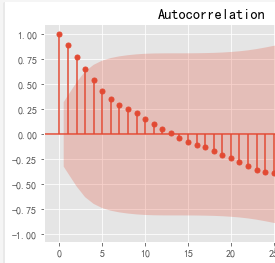
在这里插入图片描述

平稳性检验

print(‘原始序列的ADF检验结果为’,ADF(sale[‘销量’]))
#解读：P值（第二个）大于显著性水平α（0.05），接受原假设（非平稳序列），说明原始序列是非平稳序列。

在这里插入图片描述

（三）一阶差分序列的检验

#方法：单位根检验
# print(‘原始序列的ADF检验结果为’,ADF(sale[‘销量’]))

d1_sale=sale.diff(periods=1, axis=0).dropna()
d1_sale=d1_sale['销量']
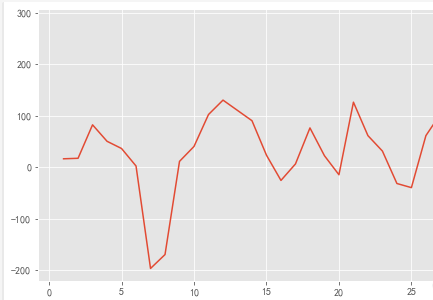
#时序图
plt.figure(figsize=(10,5))
d1_sale.plot()
plt.show()
#解读：在均值附件比较平稳波动

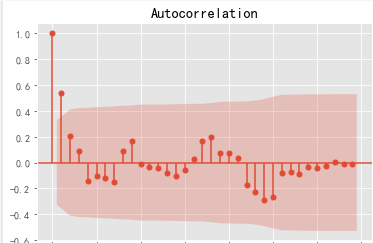
#自相关图
plot_acf(d1_sale,lags=34).show()
#解读：有短期相关性，但趋向于零。

#平稳性检验
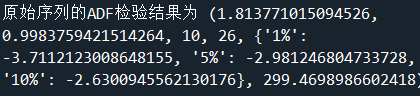
print('原始序列的ADF检验结果为：',ADF(d1_sale))

#解读：P值小于显著性水平α（0.05），拒绝原假设（非平稳序列），说明一阶差分序列是平稳序列。

在这里插入图片描述

在这里插入图片描述
平稳性检验ADF小于0.05，说明一阶差分是平稳的

白噪声检验

print(‘一阶差分序列的白噪声检验结果为：’,acorr_ljungbox(d1_sale,lags=1))#返回统计量、P值
#解读：p值小于0.05，拒绝原假设（纯随机序列），说明一阶差分序列是非白噪声。

在这里插入图片描述
p值小于0.05，拒绝原假设（纯随机序列），说明一阶差分序列是非白噪声。

（四）定阶（参数调优）

确定P值和Q值

# 参数调优：BIC
# # 模型调优的方法：AIC和BIC
# # 值越小越好
# # 参数调优的方法非常多，用不同方法得出的结论可能不同
# from pandas.core.frame import DataFrame
# pmax=int(len(d1_sale)/10) #一般阶数不超过length/10
# qmax=int(len(d1_sale)/10) #一般阶数不超过length/10
# bic_matrix=[]
# for p in range(pmax+1):
# tmp=[]
# for q in range(qmax+1):
# try:
# tmp.append(ARIMA(sale,(p,1,q)).fit().bic)
# except:
# tmp.append(None)
# bic_matrix.append(tmp)
# p,q=DataFrame(bic_matrix).stack().idxmin() #最小值的索引
# print(‘用BIC方法得到最优的p值是%d,q值是%d’%(p,q))

# pmax=int(len(d1_sale)/10) #一般阶数不超过length/10
# qmax=int(len(d1_sale)/10) #一般阶数不超过length/10

# aic_matrix=[]
# for p in range(pmax+1):
#     tmp=[]
#     for q in range(qmax+1):
#         try:
#             tmp.append(ARIMA(sale,(p,1,q)).fit().aic)
#         except:
#             tmp.append(None)
#     aic_matrix.append(tmp)
# aic_matrix=pd.DataFrame(aic_matrix)
# p,q=aic_matrix.stack().idxmin() #最小值的索引
# print('用AIC方法得到最优的p值是%d,q值是%d'%(p,q))

用AIC和BIC方法得到的最优的P值和Q值为0,1

（五）建模与预测

#构建模型
model=ARIMA(sale[‘销量’],(0,1,1)).fit()
#查看模型报告
print(model.summary2())

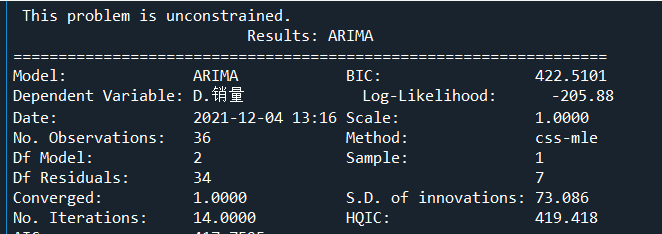
在这里插入图片描述

残差检验

#残差检验
#自相关图
resid=model.resid
plot_acf(resid,lags=35).show()

#解读：有短期相关性，但趋向于零。

#偏自相关图
plot_pacf(resid,lags=20).show()

#偏自相关图
plot_pacf(resid,lags=35).show()
#

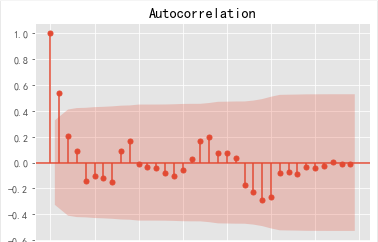
在这里插入图片描述

如图所示一阶，二阶，三阶都是非常小的数，说明它们之间的相关性比较小，可能是一个纯随机序列

#qq图：线性即正态分布
qqplot(resid, line=‘q’, fit=True).show()
#解读：残差服从正态分布，均值为零，方差为常数

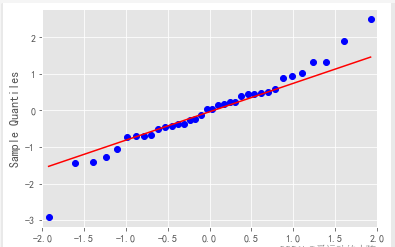
在这里插入图片描述

上图可以看出数据均匀的落在直线的周围，说明数据服从正态分布：均值为0，方差为常数，是一个纯随机序列。

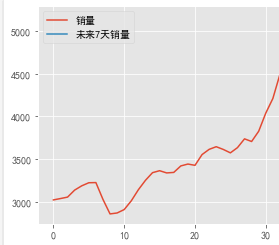
预测

print(‘未来七天的销量数据：\n’)
print(model.forecast(7))

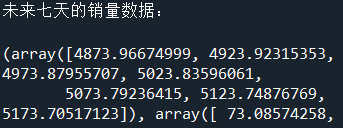
在这里插入图片描述

#预测
# print(‘未来七天的销量数据：\n’)
# print(model.forecast(7))
forecast=pd.Series(model.forecast(7)[0],index=pd.date_range(‘2015-2-7’,periods=7,freq=‘D’))
data=pd.concat((sale,forecast),axis=0)
data.columns=[‘日期’,‘销量’,‘未来7天销量’]
plt.figure(figsize=(10,5))
data[[‘销量’,‘未来7天销量’]].plot()
plt.show()

在这里插入图片描述