英文题目：CausalEGM: a general causal inference framework by encoding generative modeling

中文题目：CausalEGM：通过编码生成建模的通用因果推理框架

单位：斯坦福大学统计系

时间：2023

论文链接：https://arxiv.org/pdf/2212.05925.pdf

代码：https://github.com/SUwonglab/CausalEGM

摘要：

尽管理解和表征因果效应在观察性研究中变得至关重要，但当协变量高维时，它具有挑战性。在本文中，我们开发了一个通用框架 CausalEGM，用于通过编码生成建模来估计因果效应，该框架可以应用于二进制和连续处理设置。在具有无混淆的潜在结果框架下，我们在高维协变量空间和已知密度的低维潜在空间之间建立双向转换（例如，多元正态分布）。通过这种方法，CausalEGM同时解耦协变量对治疗和结果的依赖性，并将协变量映射到低维潜在空间。通过对低维潜在特征的条件，CausalEGM 可以估计每个个体的因果影响或人群中的平均因果效应。我们的理论分析表明，CausalEGM 的超额风险可以通过经验过程理论来限制。在编码器-解码器网络的假设下，可以保证估计的一致性。在一系列实验中，CausalEGM 在二元和连续处理方面都表现出优于现有方法的性能。具体来说，我们发现 CausalEGM 在样本量大和高维协变量存在的情况下比竞争方法更强大。CausalEGM 的软件可在 https://github.com/SUwonglab/CausalEGM 免费获得。

1简介

鉴于观察数据，对治疗因果效应的推论对于许多科学和工程问题至关重要，并引起了广泛的兴趣。例如，(1) Zhang et al.(2017)研究了药物对个性化医疗健康结果的影响;(2) Panzzia和Presbitero(2014)评估了政府公共政策的有效性;(3) Kohavi和Longbotham(2017)进行了A/B测试，为商业公司选择更好的推荐策略。从历史上看，许多数据集的小样本大小阻碍了通过传统亚组分析有意义地探索治疗效果。在大数据时代，数据积累激增。因此，我们需要更强大的工具来准确估计大规模观测数据的因果影响。

研究人员对学习因果关系比因果推理的相关性更感兴趣。学习因果关系最有效的方法是进行随机对照试验 (RCT)，其中受试者被随机分配到接受治疗/干预的实验组和一个对照组进行比较。那么结果的实验组和对照组之间的差异衡量了治疗/干预的有效性。RCT 已成为研究因果关系的黄金标准，因为随机化可能会限制各种偏差。然而，RCT 是耗时、昂贵且有问题的，具有普遍性（RCT 中的参与者并不总是代表他们的人口）。相比之下，观察性研究可以提供有价值的证据并检查“现实世界”设置中的影响，而 RCT 倾向于评估高度选定人群中理想条件下的治疗效果。给定观测数据，我们知道每个个体的治疗、结果和协变量。需要发现治疗对结果有因果关系的机制。一个目标是估计反事实的结果。例如，“如果患者/她接受了不同的治疗，这个患者是否会有不同的健康状况？”在实际应用中，由于混杂因素引入的选择偏差，治疗通常不会随机分配。因此，处理过的人群可能与一般人群有很大不同。因果效应的准确估计涉及处理混杂因素，即影响治疗和结果的变量。未能调整混淆效应可能会导致估计偏差和错误的结论。

已经提出了许多框架来解决上述问题。Rubin (1974) 和 Splawa-Neyman et al. (1990) 的潜在结果模型，也称为 Neyman-Rubin 因果模型，可以说是使用最广泛的框架。它对因果关系和潜在假设进行了精确的推理。为了衡量治疗的因果影响，我们需要比较每个个体的事实和反事实结果。由于不可能在不同的治疗条件下观察同一个体的潜在结果，推理任务可以看作是一个“缺失数据”问题，其中需要估计反事实结果。一旦我们在个人或人口平均水平解决“缺失数据”问题，就可以估计相应的个体因果效应或平均因果效应。

潜在结果框架下因果效应非参数估计的经典方法包括重新加权、匹配和分层，详细参见评论文章 Imbens (2004)。当协变量的维度较低时，这些方法通常表现良好，但当协变量的数量很大时会崩溃。近年来，机器学习的繁荣在很大程度上加速了因果推理算法的发展。在本文中，我们探索了机器学习（尤其是深度学习）的进步，以提高因果效应估计的性能。具体来说，我们探索了如何应用深度生成模型将高维协变量映射到具有所需分布的潜在空间。所提出的降维方案能够对低维潜在特征进行调节，这为处理高维协变量提供了新的见解。

1.1相关工作

我们的工作有助于文献使用深度生成模型估计因果效应。该领域的大多数工作都是在二元处理设置下进行的。例如，重新加权方法，例如Rosenbaum(1987)的IPW，Robins等人(1994)为每个单元分配适当的权重以消除选择偏差。基于匹配的方法提供了一种直接比较匹配样本中处理组和对照组的结果的解决方案。Stuart (2010) 中可以找到匹配方法的详细回顾。

因果推理中另一种流行的方法是基于决策树。这些基于树的方法通过学习从数据中学习决策规则来使用非参数分类或回归。请参阅 Athey 和 Imbens (2016)、Hill (2011) 和 Wager 和 Athey (2018)。

最近，神经网络已应用于因果推理，展示了令人信服的和有希望的结果。参见Shalit等人(2017)、Shi等人(2019)、Louizos等人(2017)和Yoon等人(2018)。这些努力中的大多数都处于二元处理设置下。这些方法存在一些局限性。首先，这些模型通常使用单独的网络来估计不同处理条件下的结果函数。这种特定于治疗的网络很难推广到连续治疗。其次，这些基于神经网络的方法侧重于最小化反事实结果的预测误差，同时缺乏足够的理论分析来解释模型设计和架构的合理性。

至于处理连续处理的方法，很多努力都集中在开发 Hirano 和 Imbens (2004) 的广义倾向得分理论。有关其他基于回归的模型，请参见双鲁棒估计器 Robins 和 Rotnitzky (2001)、基于树的方法 Hill (2011)、Lee (2018) 和 Galagate (2016)。还有一些非参数方法不需要正确规范将治疗或结果与协变量联系起来的模型。参见Flores等人(2007)、Kennedy等人(2017)、Fong等人(2018)和Colangelo和Lee(2020)。然而，大多数基于回归的方法需要对协变量和治疗或结果之间的关系进行限制性条件。例如，Galagate (2016) 只考虑平均剂量响应函数 (ADRF) 是二次的情况。Fong等人(2018)依赖于治疗与协变量呈线性关系的假设。这种强有力的假设阻碍了这些方法的广泛应用。根据经验，这些方法中的许多在存在高维协变量的情况下失败，并且不能扩展到大规模数据集。

为了克服上述限制，我们开发了 CausalEGM，这是一种使用编码生成建模估计治疗效果的通用框架。CausalEGM 模型在以下方面与现有方法不同。1）CausalEGM 没有使用特定于治疗的网络，而是利用了一个统一的模型架构，该架构适用于离散和连续处理设置。2) CausalEGM采用编码生成降维方案，将协变量对治疗和结果的依赖性解耦，而大多数现有方法无法区分依赖关系。3) CausalEGM 不假设任何预规范处理模型和结果模型。综上所述，本文的主要贡献是提出了一个新的框架，通过编码生成方案将高维协变量映射到低维潜在特征。通过也就是说，使用对抗训练具有所需分布的潜在特征使得它很容易条件。统一的模型设计还支持二进制和连续处理设置下的治疗效果估计。基准数据集的一系列系统实验表明，我们的框架在各种设置下优于最先进的方法。

2 方法

2.1问题表述

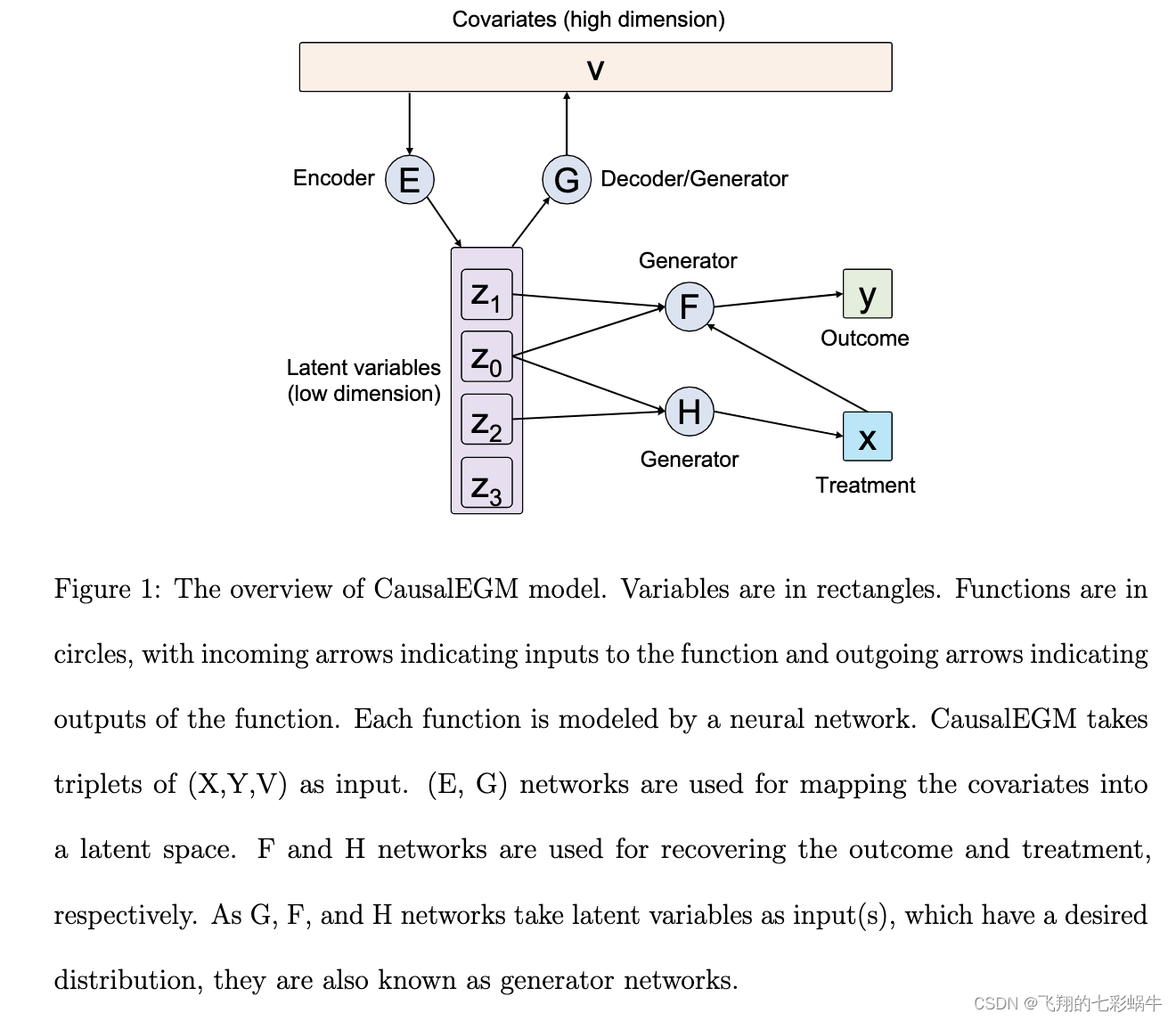 2.2因果推理的编码生成模型

2.3模型训练

CausalEGM 模型由双向转换模块和两个前馈神经网络组成。双向转换模块用于将协变量投影到低维空间并解耦依赖关系。这个双向模块由两个生成对抗网络 (GAN) 组成。在一个方向上，编码器网络E旨在将协变量转换为潜在特征，其分布与标准多元高斯分布相匹配。鉴别器 Dz 网络试图将从多元高斯分布（标记为正高斯分布）中采样的数据与 E 网络生成的数据区分开来（标记为零）。类似地，GAN 模型中还有另一个鉴别器网络以相反的方向工作，其中生成器/解码器网络 G 将潜在特征转换回原始协变量空间以匹配协变量的经验分布。鉴别器网络 D 可以被认为是一个二元分类器，其中潜在多元正态的 D(x) = 1，对于来自经验数据分布的编码器诱导的分布，D(x) = 0。我们使用 WGAN-GP (Gulrajani et al., 2017) 作为 GAN 实现的架构，其中判别器的梯度惩罚被视为一个额外的损失项。因此，对抗训练在潜在空间中分布匹配的损失函数为两项

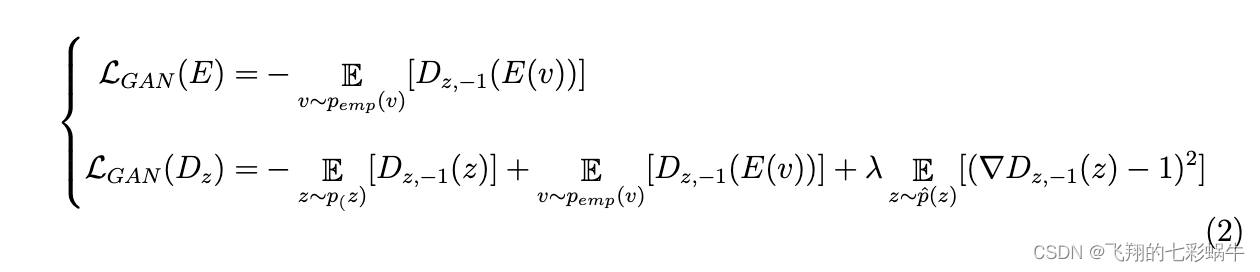
 2.4模型架构

CausalEGM 的架构非常灵活。在这项工作中，我们对所有网络使用全连接层。具体来说，(E, G, F, H) 网络包含 5 个全连接层，每层有 64 个隐藏节点。(Dz , Dv) 网络每个网络分别包含 3 个全连接层，分别有 64、32、8 个隐藏节点。leaky-ReLu 激活函数部署为每个隐藏层中的非线性变换。当处理为二进制时，我们使用 Sigmoid 作为 H 网络最后一层的激活函数。对于连续处理，我们不使用任何激活函数。批量归一化（Ioffe 和 Szegedy，2015）应用于鉴别器网络。我们使用初始学习率为 2 × 10−4 的 Adam 优化器 (Kingma and Ba, 2015)。模型参数以小批量方式更新，批量大小为 32。训练迭代的默认数量为 30,000。

3理论分析

3.1 GAN背景

3.2问题设置和符号

4 实验

我们进行了一系列实验来评估 CausalEGM 对某些最先进方法的性能。在观察性研究中，准确估计治疗对人口水平和个体水平的影响都是至关重要的。我们的目标是验证CausalEGM估计对人口水平的平均治疗效果和对异质治疗效果的个体治疗估计的能力。由于 CausalEGM 适用于二元处理和连续处理，我们测试了 CausalEGM 在两种设置下的性能。

4.1 数据集

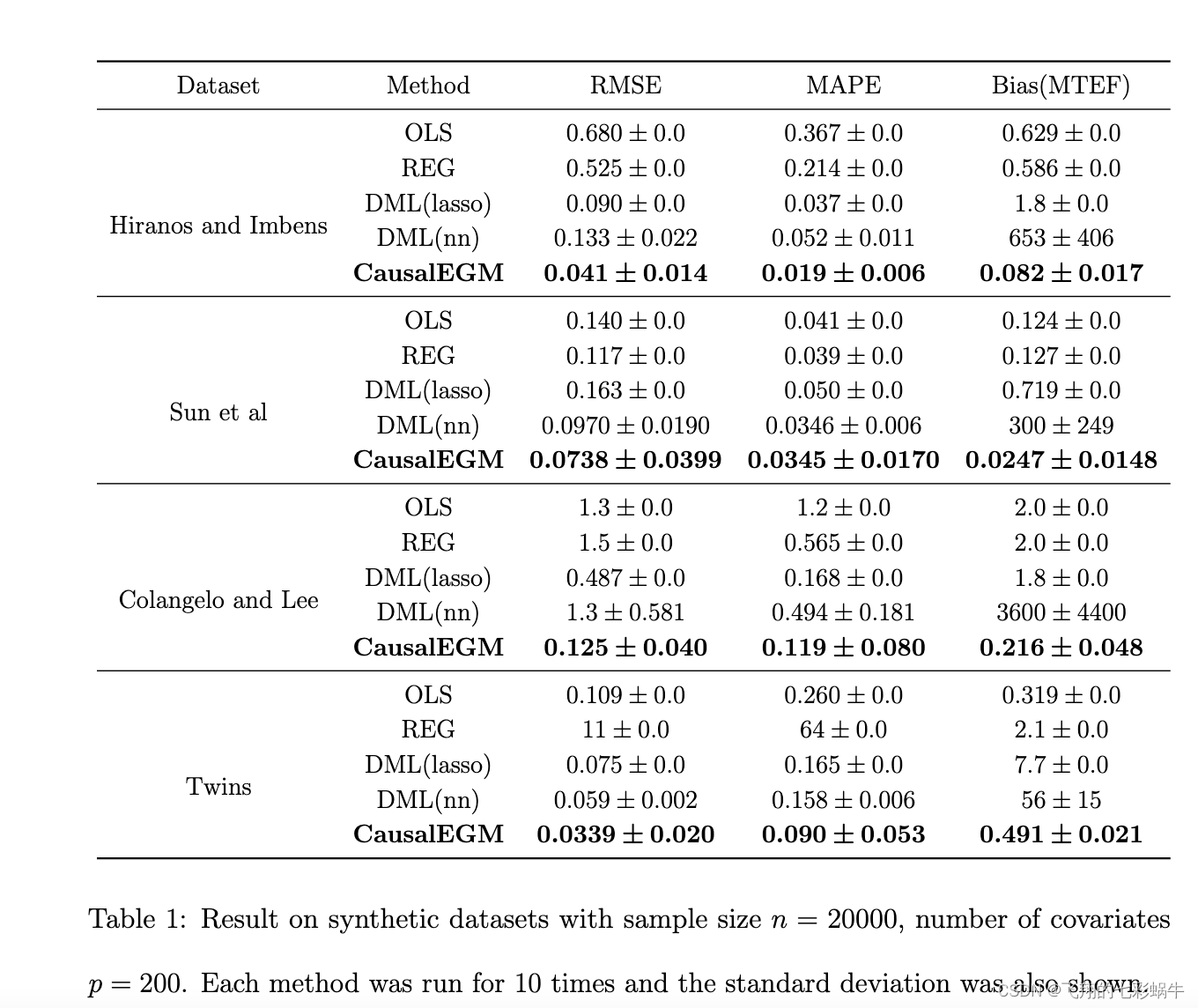
对于连续处理设置，将使用来自先前出版物的三个模拟数据集和真实数据集。

4.2评估指标

4.3 基线 

对于连续处理设置，使用了三个不同的基线。

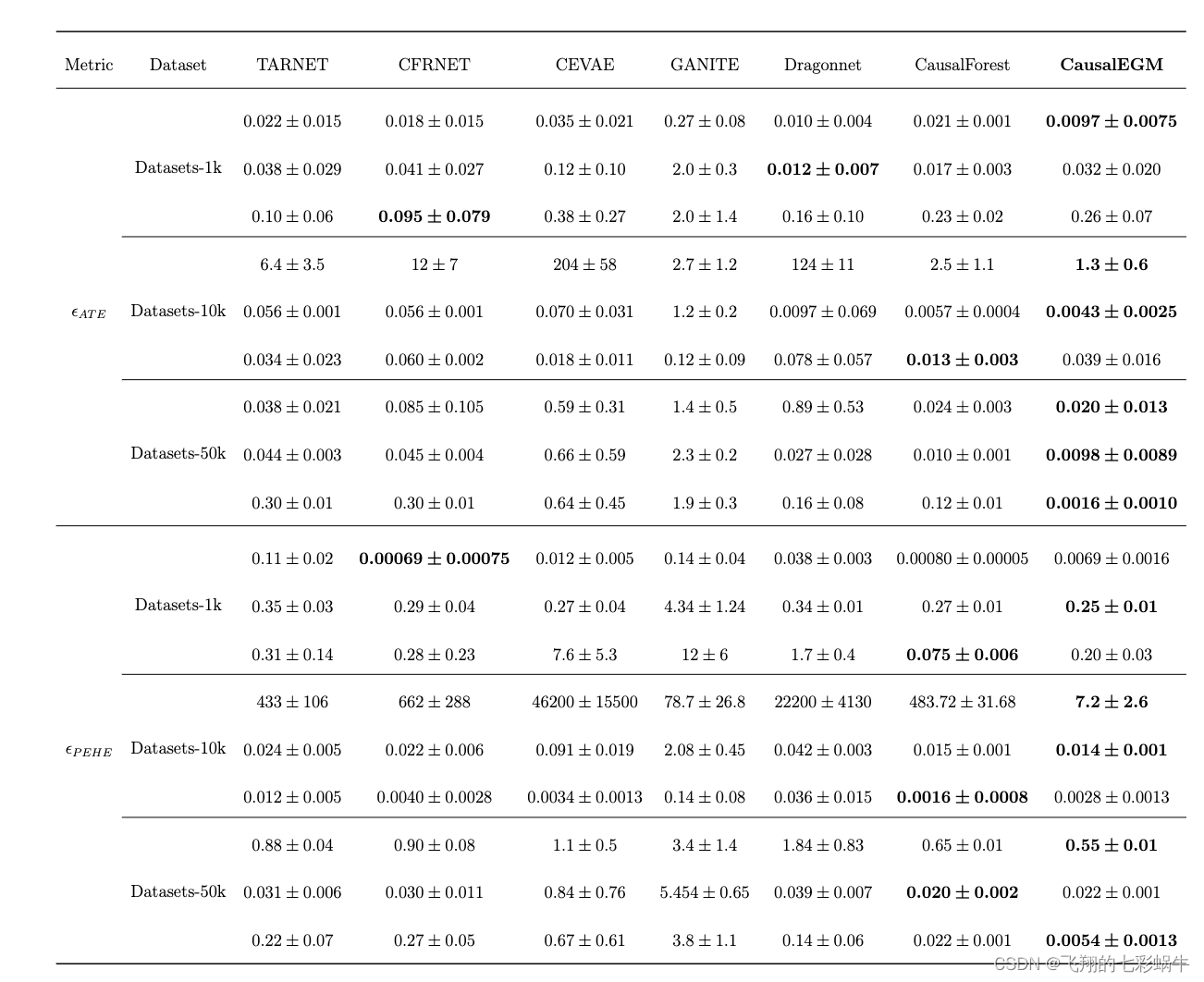
对于二元处理设置，引入了五个基线。

 

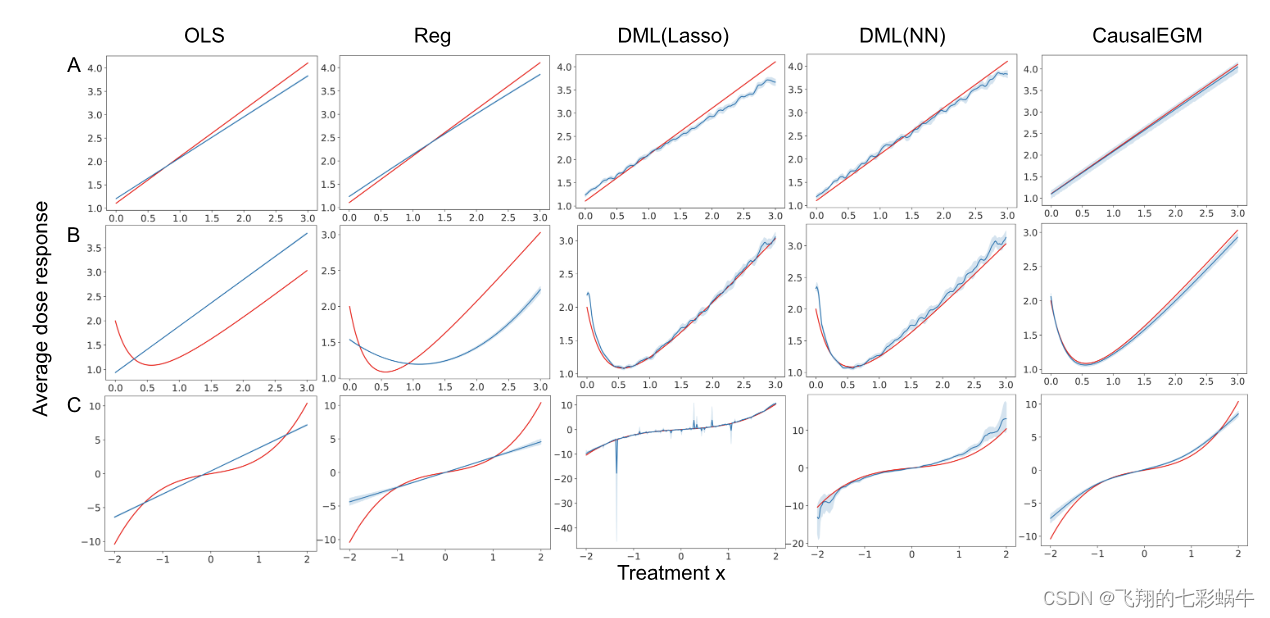
 4.4结果

 

 5 结论

 在本文中，我们开发了一种新的 CausalEGM 模型，该模型利用深度生成模型的进步来处理混杂因素并估计因果推理中的治疗效果。CausalEGM实现了高效的编码，映射高维协变量到低维潜在空间。我们使用基于 GAN 的对抗训练和基于自动编码器的重建来保证潜在特征彼此独立，并包含协变量的必要变化以进行良好的重建。CausalEGM可以灵活地估计二元或连续处理设置下个体和种群的治疗效果。

在一系列系统实验中，CausalEGM 表现出优于其他现有方法的卓越性能。CausalEGM 模型的一些扩展和改进留待。在这里，我们为进一步探索提供了几个方向。首先，虽然我们使用基于 GAN 的对抗训练来保证潜在特征中的独立性，但值得尝试在生成过程中结合近似误差来分析 CausalEGM 收敛的行为。其次，当应用于具有不同样本大小的数据集时，研究 CausalEGM 中超参数的复杂性应该很有希望。

 

参考

深度因果推断模型 - CausalEGM - 知乎