目录
- 一.搜索二叉树的特性与实现
- 1.特点
- 2.实现
- 二.搜索二叉树的性能
一.搜索二叉树的特性与实现
1.特点
二叉搜索树是特殊的二叉树,它有着更严格的数据结构特点:
(1)非空左子树的所有键值小于其根结点的键值。
(2)非空右子树的所有键值大于其根结点的键值。
(3)左、右子树都是二叉搜索树
如下图所示就是一株典型的搜索二叉树:
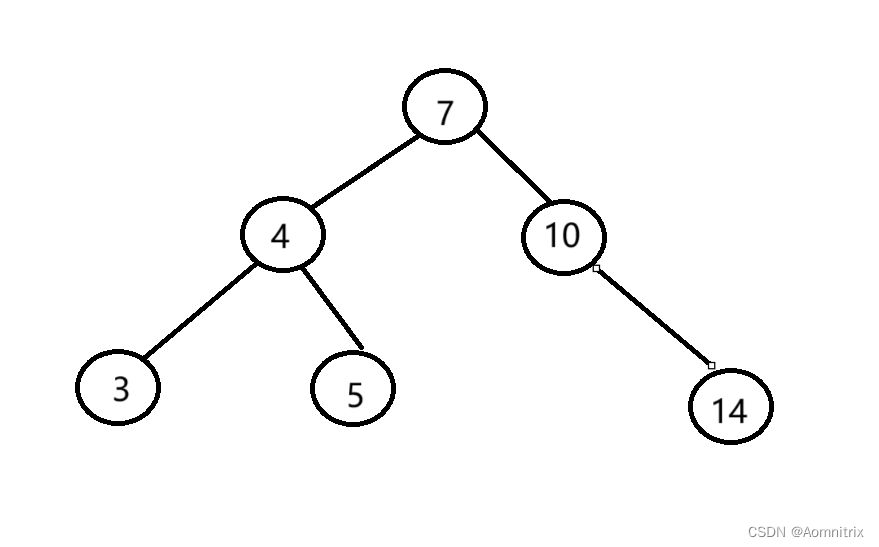
这种结构中序遍历的结果是升序的,以上特性可以帮助我们解决很多问题。例如查找
2.实现
搜索二叉树的查找功能逻辑较简单,根据要查找的值依次与当前节点键值比较,如果小于就在左树继续寻找反之在右树查找。
bool find(const T& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key > key)
{
cur = cur->left;
}
else if (cur->_key < key)
{
cur = cur->right;
}
else
{
return true;
}
}
return false;
}
插入功能首先要查找到要插入的值应该放的地方,接着判断自己是父节点的左树还有右树然后进行插入,当查找到与要插入的值相同的键值时,插入失败,因为搜索二叉树不允许有相同的值存在,需要注意的是当此树为空树时,直接插入值即可:
bool Insert(const T& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* cur = _root;
Node* parents = nullptr;
while (cur)
{
if (cur->_key < key)
{
parents = cur;
cur = cur->right;
}
else if (cur->_key > key)
{
parents = cur;
cur = cur->left;
}
else
{
return false;
}
}
cur = new Node(key);
if (parents->_key > key )
{
parents->left = cur;
}
else
{
parents->right = cur;
}
return true;
}
需要重点理解是接下来的删除功能:要删除某个键值 首先需要找到这个结点,大体逻辑与find功能相似,不同的是在找到时如何删除这个结点。这时候分为三种情况:结点左子树为空/结点右子树为空/左右子树都不为空。左或右子树为空时逻辑较简单使用托孤法即可,首先判断是否为根节点如果是则直接将根节点赋值为根节点的右或左结点接着判断自己是父节点的左/右结点,接着让父节点的左/右直接指向我的左或右结点。 当左右子树都不为空时需要使用到替换法,将要删除的结点与左子树的最大结点的键值或者右子树的最小节点的键值替换(因为要保证搜索二叉树的特性),之后删除即可。
bool Erase(const T& key)
{
Node* cur = _root;
Node* parents = nullptr;
if (cur == nullptr)
return false;
while (cur)
{
if (cur->_key > key)
{
parents = cur;
cur = cur->left;
}
else if (cur->_key < key)
{
parents = cur;
cur = cur->right;
}
else
{
if (cur->left == nullptr)
{ if (cur == _root)
{
_root = cur->right;
}
else
{
if (parents->left == cur)
{
parents->left = cur->right;
}
else
{
parents->right = cur->right;
}
}
}
else if (cur->right == nullptr)
{
if (cur == _root)
{
_root = cur->left;
}
else
{
if (parents->left == cur)
{
parents->left = cur->left;
}
else
{
parents->right = cur->left;
}
}
}
else//左子树和右子树都不为空
{
Node* parents = cur;
Node* leftmax = cur->left;
while (leftmax->right)
{
parents = leftmax;
leftmax = leftmax->right;
}
swap(cur->_key, leftmax->_key);
if (parents->left == leftmax)
{
parents->left = leftmax->left;
}
else
{
parents->right = leftmax->left;
}
cur = leftmax;
}
delete cur;
return true;
}
}
return false;
}
以上讲解的是非递归版的实现,递归版的查找 插入 删除代码更为简洁,但是更难理解。
因为在类外调用成员函数无法向函数传参成员变量,所以在类中进行一些封装:
public:
bool findR(const T& key)
{
return _findR(_root, key);
}
private:
bool _findR(Node* root, const T& key)
{
if (root == nullptr)
{
return false;
}
if (root->_key > key)
{
return _findR(root->left, key);
}
else if (root->_key < key)
{
return _findR(root->right.key);
}
else
{
return true;
}
}
查找与删除功能同样使用了封装:
public:
bool InsertR(const T& key)
{
return _InsertR(_root, key);
}
bool EraseR(const T& key)
{
return _EraseR(_root, key);
}
private:
bool _EraseR(Node*& root, const T& key)
{
if (root == nullptr)
{
return false;
}
if (root->_key > key)
{
return _EraseR(root->left, key);
}
else if (root->_key < key)
{
return _EraseR(root->right,key);
}
else
{
Node* del = root;
if (root->left == nullptr)
{
root = root->right;
}
else if (root->right == nullptr)
{
root = root->left;
}
else
{
Node* leftMax = root->left;
while (leftMax->right)
{
leftMax = leftMax->right;
}
swap(root->_key, leftMax->_key);
return _EraseR(root->left, key);
}
delete del;
return true;
}
}
bool _InsertR(Node*& root, const T& key)
{
if (root == nullptr)
{
root = new Node(key);//神之一手
return true;
}
if (root->_key > key)
{
return _InsertR(root->left, key);
}
else if (root->_key < key)
{
return _InsertR(root->right.key);
}
else
{
return false;
}
}
二.搜索二叉树的性能
查找的性能在搜索二叉树为完全二叉树或者满二叉树或者接近时,时间复杂度是logN,
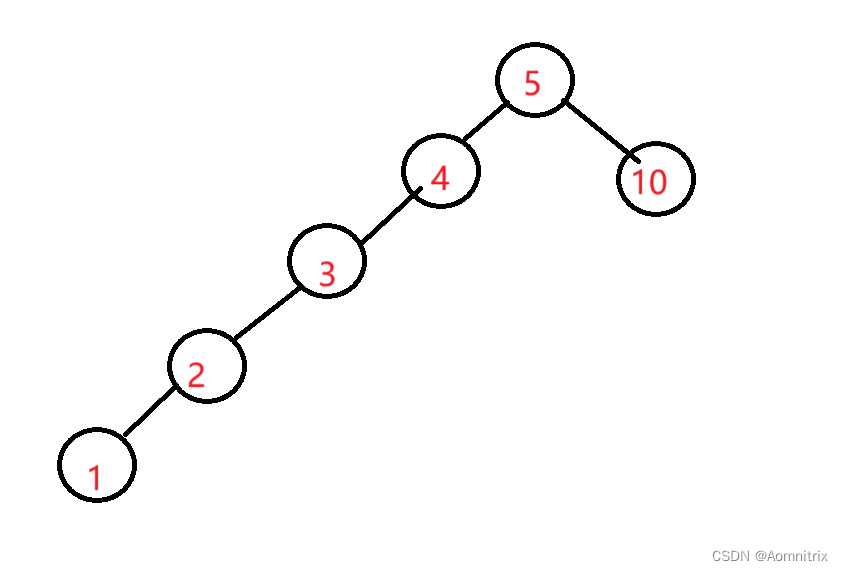
在极端情况下,时间复杂度平均为N/2.

![【C++题解】[NOIP2018]龙虎斗](https://img-blog.csdnimg.cn/img_convert/2ab72ad23f99ae8b38e39a25338499ef.png)