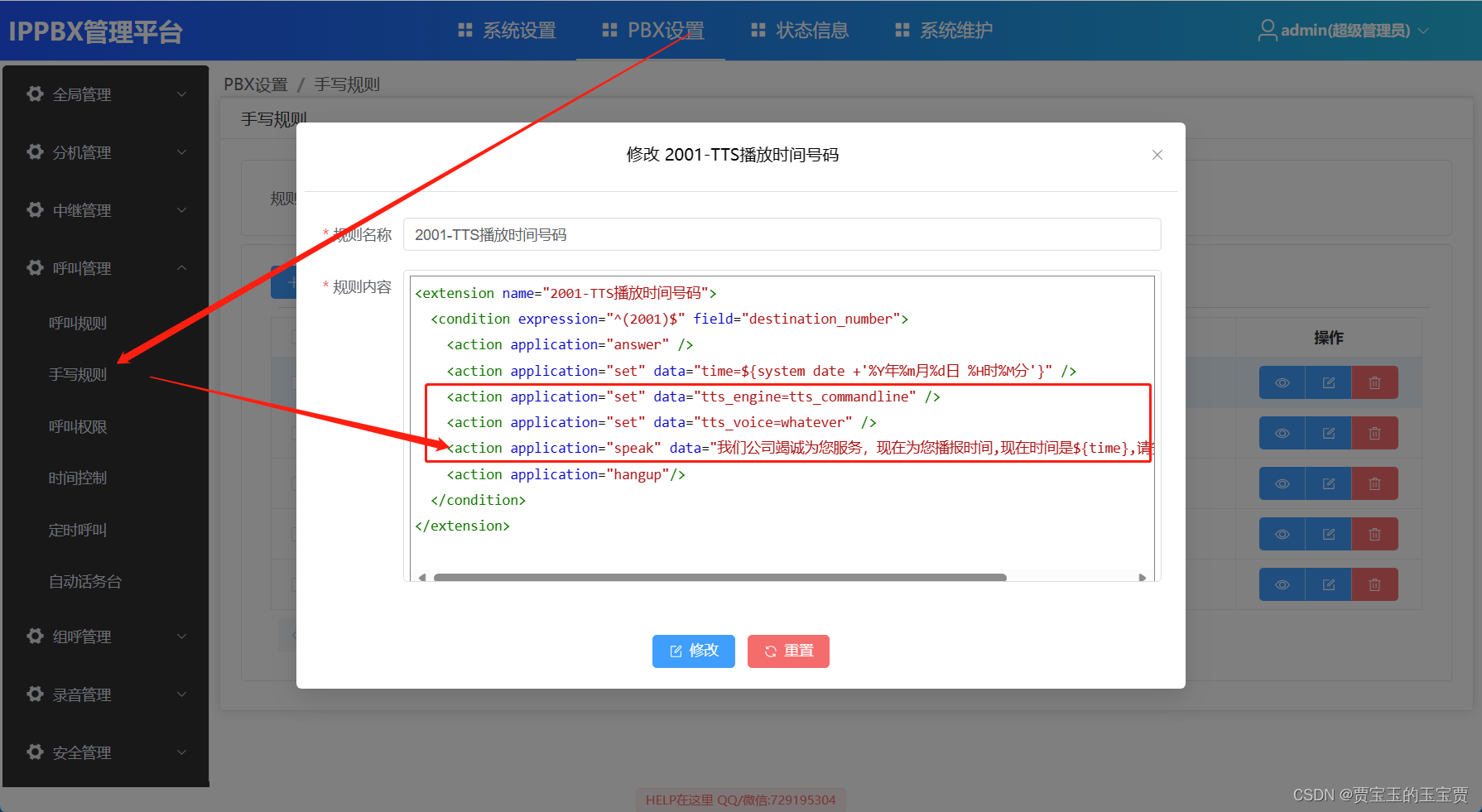
2022 ICPC 南京 M. Drain the Water Tank(叉积 + 思维)

Problem - M - Codeforces

大意：给一个多边形 ，多边形充满水 ， 点集逆时针给出 ， 求最少的出水阀门的数量使得水可以全部流出。

思路：通过画图发现 ， 我们要找的局部最低点只有两种情况 ， 一种是 V 型 ， 另一种是U型。即：

V型：

U型：

所以不难想出一个计数思路：那就是对于每个点顺时针方向和逆时针方向寻找是否有一个纵坐标大于自己的点。即找一个局部最低点 ， 对于 U型来说我们只找纵坐标相等的逆时针方向的最后一个点。

但是这样计数会出现问题：

那就是局部最低点有的在图形内部 ， 有的在图形外部。如何处理呢？

对于 V 型 ， 由于点集逆时针给出 ， 所以 用 toleft 测试 判断下一个点是否在当前向量的左边即可。

对于 U 型 ，由于我们判断的是纵坐标相同逆时针方向的最后一个点 ， 所以它的横坐标大于前一个点的横坐标即可。

一定要注意 U 型不方便用叉积判断 ， 用坐标判断即可

#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 2e6 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;
const double eps = 1e-6;

int sign(double x){
	if(fabs(x) < eps) return 0;
	if(x > 0) return 1;
	return -1;
}

struct point{
	double x , y;
	point(){}
	point(double a , double b) : x(a) , y(b){}
}; 

double det(const point &a , const point &b){
	return a.x * b.y - a.y * b.x;
}

double toleft(point p , point a, point b) {
    point A = point(b.x - a.x , b.y - a.y); //向量ab
    point B = point(p.x - a.x , p.y - a.y); //向量ap
    return det(A , B);
}

int n;
point p[N];

inline nex(int x){ return (x + 1) % n; }
inline pre(int x){ return (x - 1 + n) % n; }

signed main(){

	cin >> n;
	for(int i = 0 ; i < n ; i ++){
		double x , y;cin >> x >> y;
		p[i] = point{x , y};
	}
	
	point xx , yy;
	
	int res = 0;
	
	for(int i = 0 ; i < n ; i ++){
		
		if(p[i].y == p[nex(i)].y) continue;
		//纵坐标相同只处理最后一个点
		
		bool tagp = 0 , tagn = 0;
		
		for(int j = pre(i) ; j != i ; j = pre(j)){
			if(p[j].y == p[i].y) continue;
			if(p[j].y >  p[i].y) {
				xx = p[j];
				tagp = 1;
				break;
			}
			if(p[j].y <  p[i].y) break;
		}//顺时针找高点
		
		for(int j = nex(i) ; j != i ; j = nex(j)){
			if(p[j].y == p[i].y) continue;
			if(p[j].y >  p[i].y) {
				yy = p[j];
				tagn = 1;
				break;
			}
			if(p[j].y <  p[i].y) break;
		}//逆时针找高点
		
		if(!tagp || !tagn) continue;//找不到退出
		
		if(p[i].y == p[pre(i)].y){// U型
			if(p[i].x > p[pre(i)].x) res += 1;
		}else{// V型
			if(sign(toleft(p[pre(i)] , p[i] , p[nex(i)])) == 1) res += 1;
		}
		
	}

	cout << res << "\n";

	return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);