基于实例的学习方法
- 动机
- 基本概念
- 基于实例的学习
- 基于实例的概念表示
- 1. 最近邻
- 最近邻的例子
- 理论结果
- 最近邻(1- NN):解释
- 问题
- K-近邻(KNN)
- KNN讨论1 :距离度量
- KNN 讨论2:属性
- KNN:属性归一化
- KNN:属性加权
- KNN讨论3:连续取值目标函数
- KNN讨论4 : k的选择
- KNN讨论5:打破平局
- KNN 讨论 6: 关于效率
- KD-Tree: ( 1) 构建
- KD-Tree: ( 2) 查询
- KNN 总览:优点与缺点
- 优点
- 缺点
- 下一个问题
- 距离加权 KNN (Distance-weighted KNN)
- 距离加权 KNN
- 回顾
- 基于实例/记忆的学习器: 4 个要素
- 1-NN
- K-NN
- 距离加权 KNN
- 扩展:局部加权回归 (Locally weighted regression)
- 局部加权回归 (例子)
- 局部加权回归
- 真实测试样例下 不同基于实例的算法表现举例
- 线性回归
- 1- 近邻
- K -近邻(k=9)
- 距离加权回归(核回归)
- 局部加权回归
- 懒惰学习与贪婪学习 Lazy learner and Eager Learner
- 不同的学习方法
- 懒惰学习vs. 贪婪学习
- 懒惰
- 贪婪
- 基于实例的学 习总结
动机
-
之前【三步走】的学习方法
- 估计问题特性(如分布)
- 做出模型假设
- LSE,Decision Tree,MAP,MLE,Naive Bayes ,…
- 找到最优的参数
-
有没有一种学习方法**不遵循【模型假设+参数估计】
-
人们通过记忆和行动来推理学习
-
思考即回忆、进行类比Thinking is reminding,making analogies
-
One takes the behavior of one’s company[近朱者赤,近墨者黑]

基本概念
-
参数化(Parametric) vs.非参数化(Non-parametric)
- 参数化:
- 设定一个特定的函数形式
- 优点:简单,容易估计和解释
- 可能存在很大的偏置:实际的数据分布可能不遵循假设的分布
- 参数化:
-
非参数化:
- 分布或密度的估计是数据驱动的(data-driven)
- 需要事先对函数形式作的估计相对更少
-
Instance-Based Learning (IBL):基于实例的学习
or Instance Based Methods (IBM):基于实例的方法 -
Memory-Based Learning :基于记忆的学习
-
Case-Based Learning :基于样例的学习
-
Similarity-Based Learning :基于相似度的学习
-
Case-Based Reasoning :基于样例的推理
-
Memory-Based Reasoning :基于记忆的推理
-
Similarity-Based Reasoning :基于相似度的推理
基于实例的学习
- 无需构建模型一一仅存储所有训练样例
- 直到有新样例需要分类才开始进行处理

基于实例的概念表示
- 一个概念
c
i
c_i
ci可以表示为:
- 样例的集合 c i = { e i 1 , e i 2 , . . . } c_i = \{e_{i1}, e_{i2},...\} ci={ei1,ei2,...},
- 一个相似度估计函数 f f f,以及
- —个阈值0
- 一个实例’a’属于概念
c
i
c_i
ci,当
- 'a’和ci的某些ej相似,并且
- f ( e j , a ) > θ f(e_j, a)>\theta f(ej,a)>θ。
1. 最近邻
-
相似度
←
→
距离
相似度\leftarrow\rightarrow距离
相似度←→距离
最近邻的例子
信用评分
分类:好/坏
特征:
- L = 延迟还款/年
- R =收入/花销
| name | L | R | G/P |
|---|---|---|---|
| A | 0 | 1.2 | G |
| B | 25 | 0.4 | P |
| C | 5 | 0.7 | G |
| D | 20 | 0.8 | P |
| E | 30 | 0.85 | P |
| F | 11 | 1.2 | G |
| G | 7 | 1.15 | G |
| H | 15 | 0.8 | P |

| name | L | R | G/P |
|---|---|---|---|
| I | 6 | 1.15 | ? |
| J | 22 | 0.45 | ? |
| K | 15 | 1.2 | ? |

距离度量:
- 缩放距离 ( L 1 − L 2 ) 2 + ( 10 R 1 − 10 R 2 ) 2 \sqrt{(L_1 - L_2)^2 + (10R_1-10R_2)^2} (L1−L2)2+(10R1−10R2)2
理论结果
- 无限多训练样本下1-NN的错误率界限:
E r r ( B y t e s ) ≤ E r r ( 1 − N N ) ≤ E r r ( B y t e s ) ( 2 − K K − 1 E r r ( B a y e s ) ) Err(Bytes)\le Err(1-NN) \le Err(Bytes)\left(2-\frac{K}{K-1}Err(Bayes)\right) Err(Bytes)≤Err(1−NN)≤Err(Bytes)(2−K−1KErr(Bayes)) - 证明很长(参照Duda et al, 2000)
- 因此1-NN的错误率不大于Bayes方法错误率的2倍
最近邻(1- NN):解释

-
Voronoi Diagram
-
Voronoi tessellation
-
也称为 Dirichlet tessellation
-
Voronoi decomposition
-
对于任意欧氏空间的离散点集合S,以及几乎所有的点x, S中一定有一个和x最接近的点
- -没有说“所有的点”是因为有些点可能和两个或多个点距离相等(在边界上)
问题

- 最近邻的点是噪音怎么办?
- 解决方法
- 用不止一个邻居
- 在邻居中进行投票 → \rightarrow →k-近邻(KNN)
K-近邻(KNN)
KNN:示例(3-NN)
| 顾客 | 年龄 | 收入(K) | 卡片数 | 结果 | 距David距离 |
|---|---|---|---|---|---|
| John | 35 | 35 | 3 | No | ( 35 − 27 ) 2 + ( 35 − 50 ) 2 + ( 3 − 2 ) 2 = 15.16 \sqrt{(35-27)^2+(35-50)^2+(3-2)^2}=15.16 (35−27)2+(35−50)2+(3−2)2=15.16 |
| Mary | 22 | 50 | 2 | Yes | ( 22 − 37 ) 2 + ( 50 − 50 ) 2 + ( 2 − 2 ) 2 = 15 \sqrt{(22-37)^2+(50-50)^2+(2-2)^2}=15 (22−37)2+(50−50)2+(2−2)2=15 |
| Hannah | 63 | 200 | 1 | No | ( 63 − 37 ) 2 + ( 200 − 50 ) 2 + ( 1 − 2 ) 2 = 152.23 \sqrt{(63-37)^2+(200-50)^2+(1-2)^2}=152.23 (63−37)2+(200−50)2+(1−2)2=152.23 |
| Tom | 59 | 170 | 1 | No | ( 59 − 37 ) 2 + ( 170 − 50 ) 2 + ( 1 − 2 ) 2 = 122 \sqrt{(59-37)^2+(170-50)^2+(1-2)^2}=122 (59−37)2+(170−50)2+(1−2)2=122 |
| Nellie | 25 | 40 | 4 | Yes | ( 25 − 37 ) 2 + ( 40 − 50 ) 2 + ( 4 − 2 ) 2 = 15.74 \sqrt{(25-37)^2+(40-50)^2+(4-2)^2}=15.74 (25−37)2+(40−50)2+(4−2)2=15.74 |
| David | 37 | 50 | 2 | Yes | - |
KNN讨论1 :距离度量


- Minkowski或 L λ L_\lambda Lλ度量: d ( i , j ) = ( ∑ k = 1 p ∣ x k ( i ) − x k ( j ) ∣ λ ) 1 λ d(i,j)=\left(\sum_{k=1}^{p}|x_k(i)-x_k(j)|^\lambda\right)^{\frac{1}{\lambda}} d(i,j)=(k=1∑p∣xk(i)−xk(j)∣λ)λ1
- 欧几里得距离 ( λ = 2 ) (\lambda=2) (λ=2) d i j = ∑ k = 1 p ( x i k − x j k ) 2 d_{ij}=\sqrt{\sum_{k=1}^{p}(x_{ik}-x_{jk})^2} dij=k=1∑p(xik−xjk)2
- 曼哈顿距离 Manhattan Distance
城市街区距离City block Dis.
出租车距离 Taxi Distance
或L1度量( λ = 1 \lambda=1 λ=1): d ( i , j ) = ∑ k = 1 p ∣ x k ( i ) − x k ( j ) ∣ d(i,j)=\sum_{k=1}^{p}|x_k(i)-x_k(j)| d(i,j)=k=1∑p∣xk(i)−xk(j)∣

- •切比雪夫距离(Chebyshev Distance)
棋盘距离(Chessboard Dis.)
L ∞ L_{\infty} L∞
d ( i , j ) = m a x k ∣ x k ( i ) − x k ( j ) ∣ d(i,j)=\underset{k}{max}|x_k(i)-x_k(j)| d(i,j)=kmax∣xk(i)−xk(j)∣ - 加权欧氏距离
Mean Censored Euclidean
Weighted Euclidean Distance
∑ k ( x j k − x j k ) 2 / n \sqrt{\sum_k(x_{jk}-x_{jk})^2/n} k∑(xjk−xjk)2/n - • Bray-Curtis Dist ∑ k ∣ x j k − x j k ∣ / ∑ k ( x j k − x j k ) \sum_{k} |x_{jk}-x_{jk}|\bigg/\sum_{k} (x_{jk}-x_{jk}) k∑∣xjk−xjk∣/k∑(xjk−xjk)
- •堪培拉距离C anberra Dist. ∑ k ∣ x j k − x j k ∣ / ( x j k − x j k ) k \frac{\sum_{k} {|x_{jk}-x_{jk}|\big/(x_{jk}-x_{jk})}}{k} k∑k∣xjk−xjk∣/(xjk−xjk)
KNN 讨论2:属性

- 邻居间的距离可能被某些取值特别大的属性所支配
- e.g.收入
D
i
s
(
J
o
h
n
,
R
a
c
h
e
l
)
=
(
35
−
45
)
2
+
(
95000
−
215000
)
2
+
(
3
−
2
)
2
Dis(John, Rachel)=\sqrt {(35-45)^2 + (95000-215000)^2+(3-2)^2}
Dis(John,Rachel)=(35−45)2+(95000−215000)2+(3−2)2
-对特征进行归一化是非常重要的(e.g.,把数值归一化到[0-1]) - Log, Min-Max, Sum,…
- e.g.收入
D
i
s
(
J
o
h
n
,
R
a
c
h
e
l
)
=
(
35
−
45
)
2
+
(
95000
−
215000
)
2
+
(
3
−
2
)
2
Dis(John, Rachel)=\sqrt {(35-45)^2 + (95000-215000)^2+(3-2)^2}
Dis(John,Rachel)=(35−45)2+(95000−215000)2+(3−2)2
KNN:属性归一化
| 顾客 | 年龄 | 收入(K) | 卡片数 | 结果 |
|---|---|---|---|---|
| John | 35/63=0.55 | 35/200=0.175 | 3/4=0.75 | No |
| Mary | 22/63=0.34 | 50/200=0.25 | 2/4=0.5 | Yes |
| Hannah | 63/63=1 | 200/200=1 | 1/4=0.25 | No |
| Tom | 59/63=0.93 | 170/200=0.85 | 1/4=0.25 | No |
| Nellie | 25/63=0.39 | 40/200=0.2 | 4/4=1 | Yes |
| David | 37/63=0.58 | 50/200=0.25 | 2/4=0.5 | Yes |
KNN:属性加权
- 一个样例的分类是基于所有属性的
- 与属性的相关性无关——无关的属性也会被使用进来
- 根据每个属性的相关性进行加权 e.g d W E ( i , j ) = ( ∑ k = 1 p w k ( x k ( i ) − x k ( j ) ) 2 ) 1 2 d_{WE}(i,j)=\left(\sum_{k=1}^{p}w_k(x_k(i)-x_k(j))^2\right)^\frac{1}{2} dWE(i,j)=(k=1∑pwk(xk(i)−xk(j))2)21
- **在距离空间对维度进行缩放 **
- wk = 0
→
\rightarrow
→消除对应维度(特征选择)
•一个可能的加权方法:
使用互信息/(属性,类别)
I ( X , Y ) = H ( X ) + H ( Y ) − H ( X , Y ) I(X,Y) = H(X)+H(Y)-H(X,Y) I(X,Y)=H(X)+H(Y)−H(X,Y) H:熵(entropy)
H ( X , Y ) = − ∑ p ( x , y ) l o g p ( x , y ) H(X,Y) = -\sum p(x,y)logp(x,y) H(X,Y)=−∑p(x,y)logp(x,y) 联合熵 (joint entropy)
- wk = 0
→
\rightarrow
→消除对应维度(特征选择)
KNN讨论3:连续取值目标函数
- 离散输出-投票
- 连续取值目标函数
- k个近邻训练样例的均值
红色:实例的真实值蓝色:估计值 红色:实例的真实值 蓝色:估计值 红色:实例的真实值蓝色:估计值

- k个近邻训练样例的均值
KNN讨论4 : k的选择
- 多数情况下k=3
- 取决于训练样例的数目
- 更大的k不一定带来更好的效果
- 交叉验证
- Leave-one-out (Throw-one-out, Hold-one-out)
- 每次:拿一个样例作为测试,所有其他的作为训练样例
- Leave-one-out (Throw-one-out, Hold-one-out)
- KNN是稳定的
- 样例中小的混乱不会对结果有非常大的影响
KNN讨论5:打破平局

- 如果k=3并且每个近邻都属于不同的类 ?
- P(W|X)=1/3 尸2
- 或者找一个新的邻居(4th)
- 或者取最近的邻居所属类
- 或者随机选一个
- 或者 …
「之后会讨论一个更好的解决方案
KNN 讨论 6: 关于效率
- KNN算法把所有的计算放在新实例来到时,实时计算开销大
- 加速对最近邻居的选择
- 先检验临近的点
- 忽略比目前找到最近的点更远的点
- 通过 KD-tree 来实现:
- KD-tree: k 维度的树 (数据点的维度是 k)
- 基于树的数据结构
- 递归地将点划分到和坐标轴平行的方形区域内
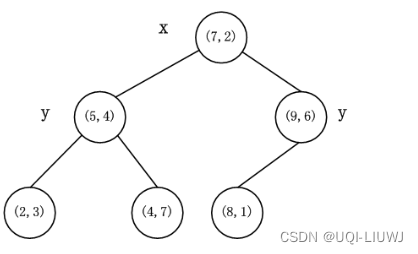
KD-Tree: ( 1) 构建
- 从一系列数据点出发

|Pt|X|Y|
| – | – | – |
|1 | 0.00|0.00|
|2 | 1.00 | 4.31|
|3 | 0.13 | 2.85 |
| … | … | …|

-
- 我们可以选择一个维度 X 和分界值 V 将数据点分为两组: X > V 和 X <= V

- 我们可以选择一个维度 X 和分界值 V 将数据点分为两组: X > V 和 X <= V
- 接下来分别考虑每个组,并再次分割(可以沿相同或不同的维度)

- 持续分割每个集合中的数据点, 从而构建一个树形结构
每个叶节点表示为一系列数据点的列表

在每个叶节点维护一个额外信息:这个节点下所有数据点的 (紧) 边界

用启发式的方法去决定如何分割
- 沿哪个维度分割?
- 范围最宽的维度
- 分割的值怎么取?
- 数据点在分割维度的中位数
- 为什么是「中位数」而不是「均值」?
- 什么时候停止分割?
- 当剩余的数据点少于 m,或者
- 区域的宽度达到最小值
KD-Tree: ( 2) 查询
- 遍历树,来查找所查询数据点的最近邻居

- 先检验临近的点 :关注距离所查询数据点最近的树的分支


- 达到一个叶节点后 :计算节点中每个数据点距离目标点的距离


接着回溯检验我们访问过的每个树节点的另一个分支

- 每次我们找到一个最近的点,就更新距离的上界

- 利用这个最近距离以及每个树节点下数据的边界信息,
我们可以对一部分不可能包含最近邻居的分支进行剪枝



KNN 总览:优点与缺点
优点
- 概念上很简单,但可以处理复杂的问题(以及复杂的目标函数)
- e.g. 图片分类
- 通过对k-近邻的平均, 对噪声数据更鲁棒
- 容易理解 :预测结果可解释(最近邻居)
- 训练样例中呈现的信息不会丢失
- 因为样例本身被显式地存储下来了
- 实现简单、稳定、没有参数(除了 k)
- 方便进行 leave-one-out 测试
缺点
- 内存开销
- 需要大量的空间存储所有样例
- 通常来说,需要存储任意两个点之间的距离 O(n2) ; K-DTrees O(nlogn)
- CPU 开销
- 分类新样本需要更多的时间(因此多用在离线场景)
- 很难确定一个合适的距离函数
- 特别是当样本是由复杂的符号表示时
- 不相关的特征 对距离的度量有负面的影响
下一个问题
- 回忆:用多个邻居使得对噪声数据鲁棒
这些邻居的贡献是一样的吗? - 解决方案
- 对数据加权
- 更接近所查询数据点的邻居赋予更大的权 → \rightarrow →距离加权近邻
距离加权 KNN (Distance-weighted KNN)
距离加权 KNN
- 一种加权函数
- wi = K(d(xi, xq))
- d(xi, xq) :查询数据点与 xi 之间的关系
- K( ·) :决定每个数据点权重的核函数
- 输出: 加权平均: p r e d i c t = ∑ w i y i / ∑ w i predict = \sum w_i y_i / \sum w_i predict=∑wiyi/∑wi
- 核函数 K(d(xi, xq))
- 1/d2, e − d e^{-d} e−d, 1/(1+d), … 应该和距离 d 成反比
回顾

距离加权 NN


基于实例/记忆的学习器: 4 个要素
- 一种距离度量
- 使用多少个邻居?
- 一个加权函数(可选)
- 如何使用已知的邻居节点?
1-NN

基于记忆的学习器:4 个要素
- 一种距离度量 欧式距离
- 使用多少个邻居? 一个
- 一个加权函数(加权) 无
- 如何使用已知的邻居节点? 和邻居节点相同
K-NN

基于记忆的学习器:4 个要素
- 一种距离度量 欧式距离
- 使用多少个邻居? K 个
- 一个加权函数(加权) 无
- 如何使用已知的邻居节点? K 个邻居节点投票
距离加权 KNN

基于记忆的学习器: 4 个要素
- 一种距离度量 缩放的欧式距离
- 使用多少个邻居? 所有的,或K 个
- 一个加权函数(可选)
w i = e x p ( − D ( x i , q u e r y ) 2 / K w 2 ) w_i = exp(-D(x_i, query)^2 / K_w^2) wi=exp(−D(xi,query)2/Kw2)
Kw :核宽度。非常重要 - 如何使用已知的邻居节点?每个输出的加权平均 p r e d i c t = ∑ w i y i / ∑ w i predict = \sum w_iy_i / \sum w_i predict=∑wiyi/∑wi
扩展:局部加权回归 (Locally weighted regression)
- 回归:对实数值目标函数做估计/预测
- 局部: 因为函数的估计是基于与所查询数据点相近的数据
- 加权:每个数据点的贡献由它们与所查询数据点的距离决定
局部加权回归 (例子)

局部加权回归

基于记忆的学习器:4 个要素
- 一种距离度量 缩放的欧式距离
- 使用多少个邻居? 所有的,或K 个
- 一个加权函数(可选)
e.g. w i = e x p ( − D ( x i , q u e r y ) 2 / K w 2 ) w_i = exp(-D(x_i, query)^2 / K_w^2) wi=exp(−D(xi,query)2/Kw2)
Kw :核宽度。非常重要 - 如何使用已知的邻居节点?
- 首先构建一个局部的线性模型。拟合
β
\beta
β 最小化局部的加权平方误差和:
β
‾
=
a
r
g
m
i
n
β
∑
k
=
1
N
w
k
2
(
y
k
−
β
T
x
k
)
2
\underline\beta=\underset{\beta}{argmin} \sum_{k=1}^{N} w_k^2(y_k-\beta^Tx_k)^2
β=βargmink=1∑Nwk2(yk−βTxk)2
那么 y p r e d i c t = β ‾ T x q u e r y y_{predict} = \underline\beta^T x_{query} ypredict=βTxquery
真实测试样例下 不同基于实例的算法表现举例
线性回归

- 连接所有点

1- 近邻

K -近邻(k=9)

距离加权回归(核回归)

选择一个合适的 Kw 非常重要,不仅是对核回归,对所有局部加权学习器都很重要
局部加权回归

懒惰学习与贪婪学习 Lazy learner and Eager Learner
不同的学习方法
- 贪婪学习

- 懒惰学习 (例如基于实例的学习)
懒惰学习vs. 贪婪学习
懒惰
-
懒惰 :等待查询再泛化
- 训练时间 :短
- 测试时间 :很长
-
懒惰学习器
- 可以得到局部估计
贪婪
-
贪婪 :查询之前就泛化
- 训练时间 :长
- 测试时间:短
-
贪婪学习器
- 对于每个查询使用相同的模型
- 倾向于给出全局估计
如果它们共享相同的假设空间,懒惰学习可以表示更复杂的函数
( e.g. H=线性函数)
基于实例的学 习总结
- 基本概念与最近邻方法
- K近邻方法
- 基本算法
- 讨论:更多距离度量;属性:归一化、加权;连续取值目标函数; k 的选择;打破平局;关于效率(K-Dtree的构建与查询)
- 距离加权的KNN
- 基于实例的学习器的四要素
- 扩展:局部加权回归
- 真实测试样例下的算法表现举例
- 懒惰学习与贪婪学习