1 关键链法和关键路径法的主要区别

1.1 关键链法和关键路径法的关注焦点不同

关键路径法（CPM）：关注项目中最长的路径，也就是所需时间最长的路径，这被称为关键路径。关键路径决定了项目的最早完成时间。
关键链法（CCM）：关注资源约束和资源分配的影响，强调资源的有效利用和优化，以减少资源瓶颈导致的项目延期。

1.2 任务时长估算不同

关键路径法（CPM）：任务时长估算通常是基于确定性的，即每个任务有确定的持续时间。
关键链法（CCM）：关键链法鼓励使用更乐观的估算，以减少人为保守估算造成的项目延期。它假设资源得到了适当的分配和管理，从而可以更快地完成任务。

1.3 缓冲区管理不同

关键路径法（CPM）：通常会使用任务间的浮动时间来设置缓冲时间，以应对延误。
关键链法（CCM）：引入了项目缓冲和资源缓冲，以减轻资源约束和不确定性带来的影响。项目缓冲用于保护项目结束时间，资源缓冲用于保护资源约束点。

1.4 资源分配不同

关键路径法（CPM）：通常忽略资源分配，只关注任务的时长和顺序。
关键链法（CCM）：强调资源约束，任务的分配和调度基于资源的有效利用，以最大程度地减少资源瓶颈。

1.5 目标不同

关键路径法（CPM）：目标是尽可能地缩短项目的总持续时间。
关键链法（CCM）：目标是在资源约束下，尽可能地减少项目的延期风险。

总的来说，关键链法更加关注资源约束和优化，强调以更乐观的方式进行任务时长估算，以及引入缓冲区来保护项目进度。相比之下，关键路径法更加关注任务的时间和顺序，以实现最短的项目完成时间。选择使用哪种方法取决于项目的性质、资源限制以及团队的实际需求。

2 关键链法和关键路径法的联系

时间管理：关键路径法和关键链法都是时间管理工具，旨在帮助项目管理者合理规划任务的时间，确保项目按时完成。
任务依赖：两种方法都考虑任务之间的依赖关系，关键路径法着重于确定最长的依赖路径，而关键链法关注资源约束下的依赖关系。
项目控制：关键路径法和关键链法都有助于项目控制和进度管理，但侧重点不同。关键路径法强调确保关键路径上的任务按时完成，而关键链法注重在资源约束下减少项目延期风险。

总之，关键链法和关键路径法在项目管理中有各自的优势和应用场景。关键路径法适用于那些不受资源限制的项目，而关键链法更适用于资源约束和不确定性较高的项目，通过优化资源利用和缓冲管理，提高项目的进度控制能力。

3 关键链法和关键路径法中其他问题总结

3.1 三点估算法是否可以用在关键链法中？

一般情况下三点估算法是用在关键路径法中的，但是这里要注意：三点估算法并不限于关键路径法中，它可以在项目管理的各种方法中使用，包括关键路径法、关键链法以及其他时间管理技术。三点估算法的主要目的是提供更准确的任务时长估计，以考虑不确定性和风险，从而更好地规划项目排程。

在关键路径法中，三点估算法通常用于计算任务的最早开始时间和最晚开始时间，以确定任务的浮动时间和关键路径。这有助于确定项目的最短完成时间。

在关键链法中，三点估算法也可以用来估算关键链任务的时长，以考虑资源约束和不确定性。关键链法强调使用更乐观的任务时长估算，以减少人为保守估算可能导致的问题，而三点估算法可以为乐观估算提供支持。

总之，三点估算法是一个通用的时间管理工具，可以在各种项目管理方法中使用，以提高任务时长估计的准确性，从而更好地应对不确定性和风险。无论是关键路径法还是关键链法，三点估算法都可以为项目管理提供有价值的支持。

3.2 关键链任务和关键路径法中的关键任务有啥区别？

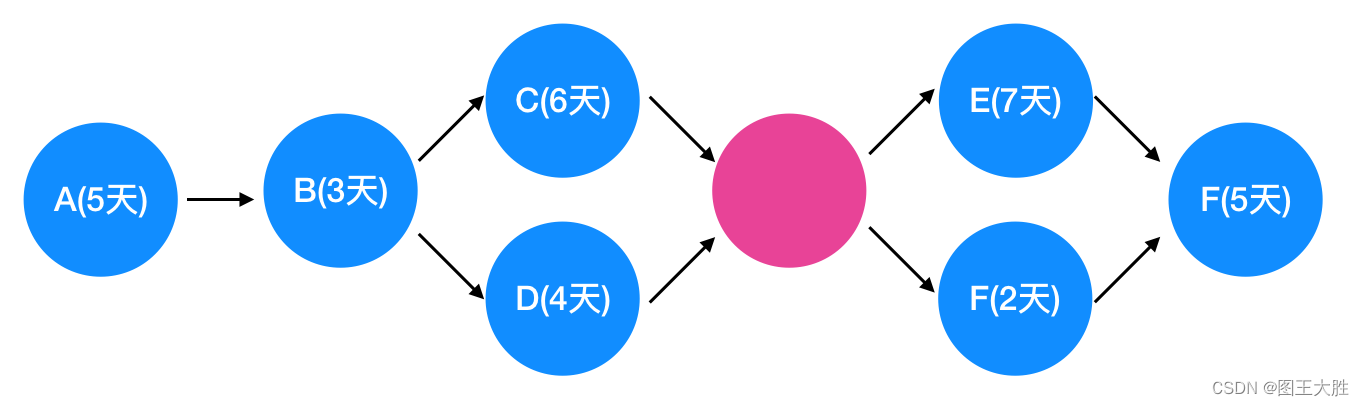
让我通过一个案例来说明关键路径法中的关键任务和关键链法中的任务之间的区别。考虑一个软件开发项目，需要完成以下几个子任务：A、B、C、D、E、F、G。每个子任务的预计完成时间和任务关系图如下（粉色为空节点，只为表达完整节点关系而引入）：

@1 关键路径法中的关键任务：

在关键路径法中，我们需要构建项目的网络图，然后找出最长路径。最长路径上的任务就是关键路径上的关键任务，它们决定了项目的最短完成时间。假设根据依赖关系，任务顺序如下：A -> B -> C、D并行 -> E、F并行 -> G。计算得出最长路径为：A -> B -> C -> E -> G，时长为 5 + 3 + 6 + 7 + 5 = 26天。因此，关键路径上的关键任务是 A、B、C、E、G。

@2 关键链法中的任务：

在关键链法中，我们考虑资源约束和缓冲管理。假设在该项目中，资源约束主要在任务 C 和任务 E 上。任务 C 需要特定的技能，而任务 E 需要特定的软件环境。这两个任务是关键链上的任务。此外，考虑乐观估算和缓冲，我们可能对任务的时长进行调整，比如任务 C 被乐观估算为 4 天，任务 E 被乐观估算为 6 天。因此，关键链法中的任务是 C 和 E。

@3 两者区别：