一、数据结构

    1.数组

        a.内存地址连续，使用之前必须要指定数组长度   

        b.可以通过下标访问的方式访问成员，查询效率高 

        c.增删操作会带来性能消耗效率相对差点(要防止数据下标越界的问题，需要动态扩容）

    2.链表 ：单向链表，双向链表LinkedList

        a.灵活的空间要求，存储空间不要求连续

        b.不支持下标访问，支持顺序遍历搜索

        c.针对增删操作找到对应的节点改变链表的头尾指向即可，无需移动元素存储位置。

    3.树 ：只有一个root节点，最底层为叶子节点

        二叉树：也可能存在不平衡二叉树

        a.某节点的左子树节点值仅包含小于该节点值

        b.某节点的右子树节点值仅包含大于该节点值

        c.左右子树每个也必须是二叉查找树

        d.顺序排列

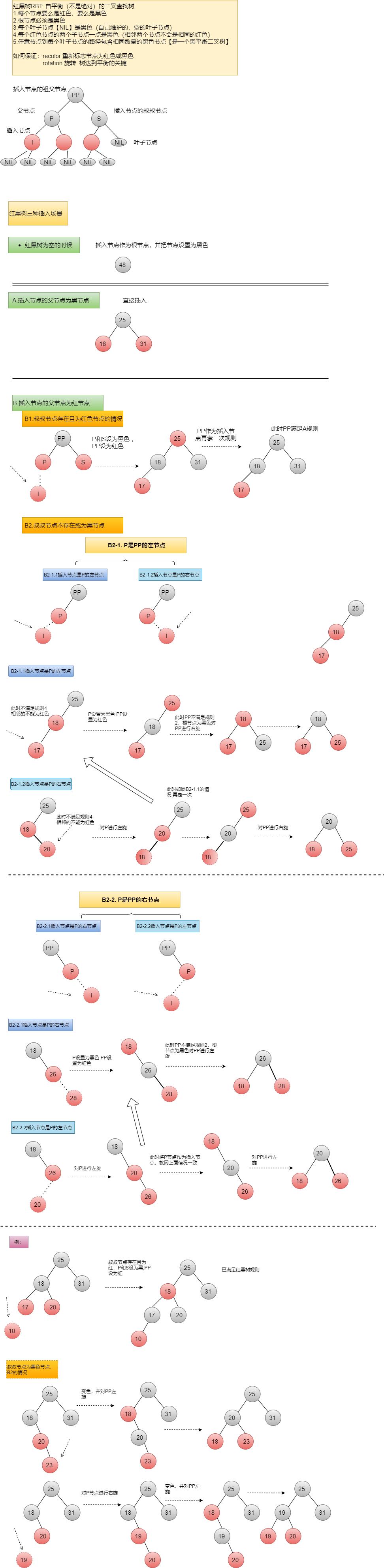
        红黑树【RBT】: 自平衡（不是绝对）的二叉查找树

        1.每个节点要么是红色，要么是黑色

        2.根节点必须是黑色

        3.每个叶子节点【NIL】是黑色（自己会维护，空的叶子节点）

        4.每个红色节点的两个子节点一定都是黑色，（相邻个节点不会是一样的红色）是黑色，（相邻个节点不会是一样的红色）

        5.任意节点到每个叶子节点的路径包含相同数量的黑节点【是一个黑平衡二叉树】

        6.通过 recolor 重新标识节点为红色或者黑色  以及 rotation旋转 树达到平衡

红黑树的插入场景：【7种】

A.红黑树为空的情况，插入进去，即为根节点，黑色

B.插入节点的父节点为黑色节点，直接将红色节点插入即可

C.插入节点的父节点为红色节点

        c.1 叔叔节点存在且为红色节点

        c.2 叔叔节点不存在或为黑色 

                c.2.1 父节点是祖父节点的左节点

                        c.2.1-1 插入节点是P的左节点

                        c.2.1-2 插入节点是P的右节点

                c.2.2 父节点是祖父节点的右节点

                          c.2.2-1 插入节点是P的右节点

                          c.2.2-2 插入节点是P的左节点

---

 

 

---