0. 前言

按照国际惯例，首先声明：本文只是我自己学习的理解，虽然参考了他人的宝贵见解，但是内容可能存在不准确的地方。如果发现文中错误，希望批评指正，共同进步。

本文的主旨是说明深度学习网络模型中关于数值稳定性的常见问题：梯度衰减（vanishing）和爆炸（explosion），以及常见的解决方法。

本文的部分内容、观点及配图借鉴了多伦多大学计算机科学学院讲座——Lecture 15: Exploding and Vanishing Gradients内容，以及Dive into deep learning第3.15章节《数值稳定性和模型初始化》。

1. 为什么会出现梯度衰减和梯度爆炸？

用下面简化的全连接神经元网络讲解，这个全连接神经元网络每层只有一个神经元，可以看作是一串神经元连接而成的网络。

在前向传播中，由于数值的传递需要经过非线性的激活函数$\sigma ()$（例如Sigmoid、Tanh函数），其数值大小被限制住了，因此前向传播一般不存在数值稳定性的问题。

在反向传播中，例如求解输出$y$对权重$w_1$的偏导为：
$$\frac{\partial y}{\partial w_1}={\sigma }^{\prime }(z_n)w_n\cdot {\sigma }^{\prime }(z_{n-1})w_{n-1}\cdot \cdot \cdot {\sigma }^{\prime }(z_1)x$$
$$z_n=\{\begin{array}{cc}{w}_n\cdot h_{n-1}+b_n,& n>1\\ w_1\cdot x+b_1,& n=1\end{array}$$
这里就可以看出，如果权重$w_n$的初始选择不合理，或者$w_n$在逐渐优化过程中，出现导致${\sigma }^{\prime }(z_n)w_n$大部分或全部大于1或者小于1的情况，且网络足够深，就会导致反向传播的偏导出现数值不稳定——梯度衰减或者梯度爆炸。

再简化点理解，假设${\sigma }^{\prime }(z_n)w_n=0.8$，有50层网络深度，$0.8^{50}=0.000014$；假设${\sigma }^{\prime }(z_n)w_n=1.2$，有50层网络深度，$1.2^{50}=9100$。

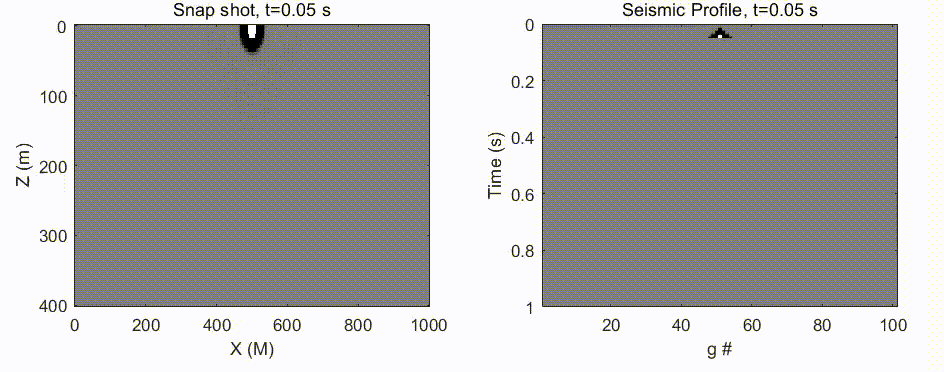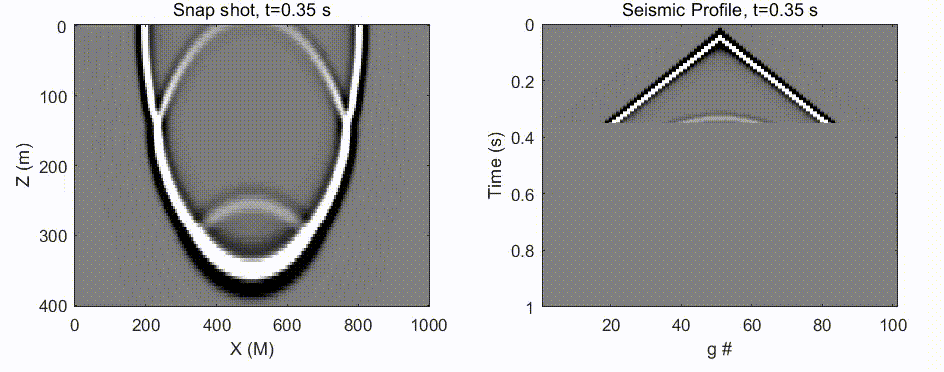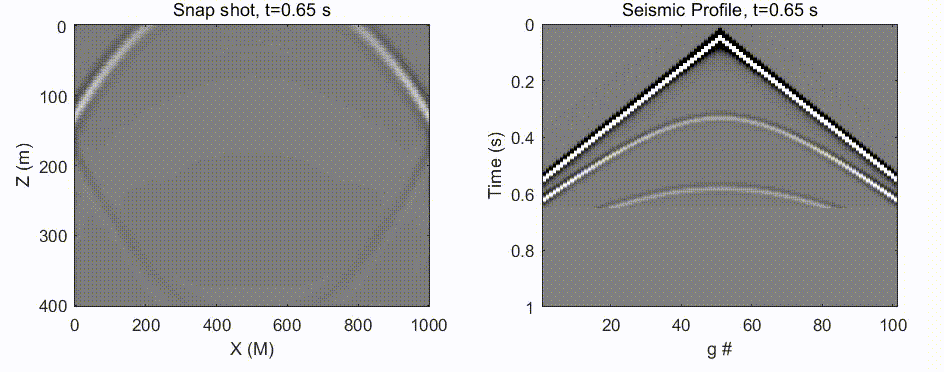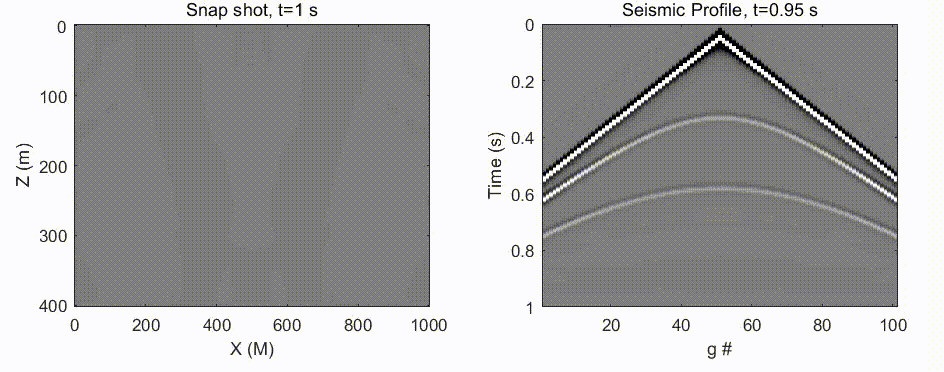
参考Lecture 15: Exploding and Vanishing Gradients的另一种解释数值稳定性的方法是：深度学习网络类似于非线性方程的迭代使用，例如$f(x)=3.5x(1-x)$经过多次迭代$y=f(f(\cdot \cdot \cdot f(x)))$后的情况如下图：

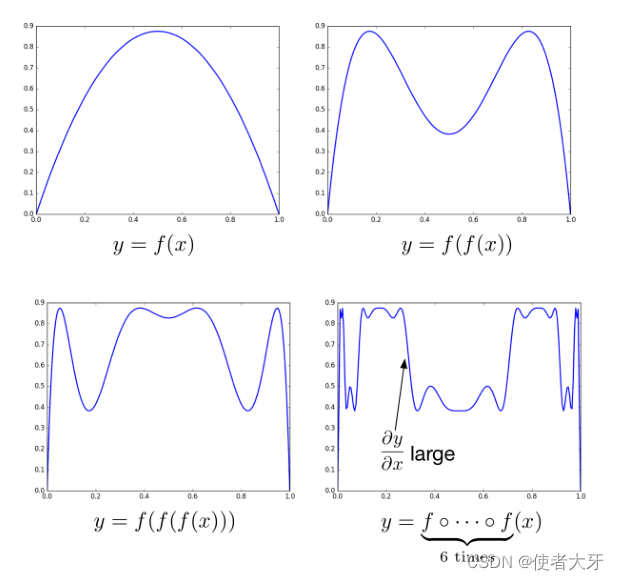
可见，非线性函数再经历多次迭代后会呈现复杂且混沌的表现，在这个实例中仅经历6次迭代后就出现了偏导很大的情况（对应梯度爆炸）。

我们也应该注意到经历6次迭代后也出现了$\frac{\partial y}{\partial x}\approx 0$的区域（对应梯度衰减）。

2. 如何提高数值稳定性？

2.1 随机初始化模型参数

这是最简单、最常用的对抗梯度衰减和梯度爆炸的方法。上文已经说明：${\sigma }^{\prime }(z_n)w_n$大部分或全部大于1或者小于1的情况，且网络足够深，就容易发生数值不稳定的情况。如果随机初始化模型参数，就会很大程度上避免因为$w_n$的初始选择不合理导致的梯度衰减或爆炸。

Xavier随机初始化是一种常用的方法：假设某隐藏层输入个数为$a$，输出个数为$b$，Xavier随机初始化会将该层中的权重参数随机采样于$(-\sqrt{\frac{6}{a+b}},\sqrt{\frac{6}{a+b}})$。

2.2 梯度裁剪（Gradient Clipping）

这是一种人为限制梯度过大或过小的方法，其思路是给原本的梯度$g$加上一个系数，在$g$的绝对值过大时对其进行缩小，反之亦然。这个系数为:
$$\frac{\eta }{||g||}$$

其中$\eta$为超参数，$||g||$为梯度的二范数。

增加这个系数后虽然会导致这个结果并非是真正的损失函数对于权重的偏导数，但是能够维持数值稳定性。

2.3 正则化

这是一种抑制梯度爆炸的方法。我之前介绍过正则化方法：基于PyTorch实战权重衰减——L2范数正则化方法（附代码），其思想是在损失函数中增加权重的范数作为惩罚项：
$$loss=\frac{1}{n}\Sigma (y-\hat{y}{)}^2+\frac{\lambda }{2n}||w|{|}^2$$
在深度学习模型不断地迭代（学习）过程中，$loss$越来越小导致权重的范数也越来越小，也就抑制了梯度爆炸。

2.4 Batch Normalization

Batch Normalization（批标准化）是基于Normalization（归一化）增加scaling和shifting的一种数据标准化处理方式，其具体作用原理可以参考：关于Batch Normalization的说明。

Batch Normalization能维持数值稳定性的基本原理与梯度裁剪类似：都是对数值人为增加缩放，维持数值保持在一个不大不小的合理范围内。两者的区别是梯度裁剪在反向传播过程中直接作用于损失函数对权重的偏导数；而Batch Normalization在正向传播中对某层的输出进行标准化处理，间接维持对权重偏导的稳定性。

这里需要指出的是：由于输入$x$也参与了偏导的计算，如果$x$是一个高维向量，那对于输入$x$的Batch Normalization处理也是必要的。

2.5 LSTM？Short Cut！

很多文章说明LSTM（长短周期记忆）网络有助于维持数值稳定性，我最初看到这些文章时大为不解——因为我们是需要通用的方法来改进提高现有模型的数值稳定性，而不是直接替换成LSTM网络模型，况且LSTM也不是万能的深度学习模型，不可能遇到梯度衰减或者梯度爆炸就把模型替换成LSTM。

如果不知道LSTM是什么可以看下：LSTM（长短期记忆）网络的算法介绍及数学推导

后来我看到Lecture 15: Exploding and Vanishing Gradients明白了其中的误解：这篇文章通篇都在用RNN为例来说明数值稳定性。对于RNN来说，LSTM确实是一个改进的模型，因为其内部维持“长期记忆”的“门”结构确实有助于提升数值稳定性。

我想大部分把LSTM单列出来说明可以提升数值稳定性的文章都误会了。

而Short Cut这种结构才是提升数值稳定性的普适规则，LSTM仅是改善RNN的一个特例而已。

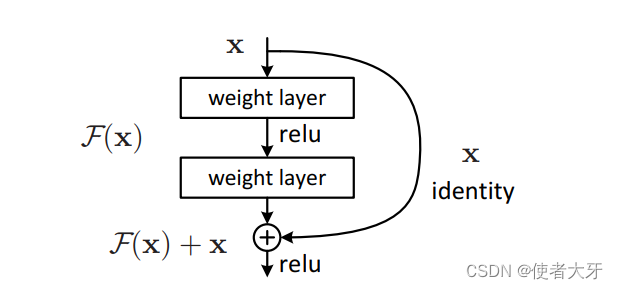
Short Cut的具体作用机理可以参考He Kaiming的原文：Deep Residual Learning for Image Recognition