应用于图像低通滤波器和高通滤波器的实现
需要用到傅里叶变换
#include <opencv2/opencv.hpp>
#include <Eigen>
#include <iostream>
#include <vector>
#include <cmath>
#include <complex>
#define M_PI 3.14159265358979323846 // pi
// 对数幅度缩放
Eigen::MatrixXd logAmplitudeSpectrum(const Eigen::MatrixXd& spectrum) {
return (spectrum.array() + 1).log();
}
// 乘幂尺度变换
Eigen::MatrixXd powerLawScaling(const Eigen::MatrixXd& spectrum, double gamma) {
return spectrum.array().pow(gamma);
}
// 归一化 to [0, 1]
Eigen::MatrixXd normalize(const Eigen::MatrixXd& spectrum) {
double minVal = spectrum.minCoeff();
double maxVal = spectrum.maxCoeff();
return (spectrum.array() - minVal) / (maxVal - minVal);
}
// 增强频谱显示
Eigen::MatrixXd enhanceSpectrumDisplay(const Eigen::MatrixXd& spectrum, double gamma = 1) {
Eigen::MatrixXd logSpectrum = logAmplitudeSpectrum(spectrum);
Eigen::MatrixXd powerScaledSpectrum = powerLawScaling(logSpectrum, gamma);
return normalize(powerScaledSpectrum);
}
// 从复数矩阵中获取幅度谱和相位谱
void getAmplitudeAndPhaseSpectra(const Eigen::MatrixXcd& data, Eigen::MatrixXd& amplitude, Eigen::MatrixXd& phase) {
amplitude = data.array().abs().matrix();
phase = data.array().arg().matrix();
}
// 从幅度谱和相位谱重构复数矩阵
void reconstructFromAmplitudeAndPhase(const Eigen::MatrixXd& amplitude,
const Eigen::MatrixXd& phase,
Eigen::MatrixXcd& data)
{
data = (amplitude.array() * (phase.array().cos() + std::complex<double>(0, 1) * phase.array().sin())).matrix();
}
// 1:**振幅谱低频移动到中心(频率平移)**:方便操作,利用象限对称互换 fft之后
Eigen::MatrixXd fftShift(const Eigen::MatrixXd &F)
{
int M = F.rows();
int N = F.cols();
Eigen::MatrixXd F_shifted(M, N);
int mid_M = M >> 1;
int mid_N = N >> 1;
// 交换第一象限和第三象限
F_shifted.block(0, 0, mid_M, mid_N) = F.block(mid_M, mid_N, mid_M, mid_N);
F_shifted.block(mid_M, mid_N, mid_M, mid_N) = F.block(0, 0, mid_M, mid_N);
// 交换第二象限和第四象限
F_shifted.block(0, mid_N, mid_M, mid_N) = F.block(mid_M, 0, mid_M, mid_N);
F_shifted.block(mid_M, 0, mid_M, mid_N) = F.block(0, mid_N, mid_M, mid_N);
return F_shifted;
}
// 2:振幅谱低频移动到中心 **图像进行-1幂操作**:然后经过fft变换后,低频会在振幅谱中间 fft之前
Eigen::MatrixXd imageShift(const Eigen::MatrixXd &image)
{
int M = image.rows();
int N = image.cols();
Eigen::MatrixXd F_shifted(M, N);
// 通过乘以 (-1)^(u+v) 来平移频率
for (int u = 0; u < M; ++u)
{
for (int v = 0; v < N; ++v)
{
//(u + v) & 1 通过位的判断末尾如果是1 为奇数,为0,为偶数。 -1的奇次幂还是-1,偶次幂为1.
F_shifted(u, v) = image(u, v) * ((u + v) & 1 ? -1 : 1);
}
}
return F_shifted;
}
Eigen::MatrixXd tMatrixXd(const cv::Mat &img)
{
Eigen::MatrixXd image(img.rows, img.cols);
for (int i = 0; i < img.rows; ++i)
{
for (int j = 0; j < img.cols; ++j)
{
image(i, j) = img.at<float>(i, j);
}
}
return image;
}
cv::Mat tMat(const Eigen::MatrixXd &img)
{
cv::Mat image(img.rows(), img.cols(), CV_32FC1);
for (int i = 0; i < img.rows(); ++i)
{
for (int j = 0; j < img.cols(); ++j)
{
image.at<float>(i, j) = img(i, j);
}
}
return image;
}
//inv =true 为逆变换,false为 正变换
//FFT 使用Eigen库中的向量表示,方便二维计算
Eigen::VectorXcd FFT(const Eigen::VectorXcd& y, bool inv = false)
{
Eigen::VectorXcd x = y;
//数据的大小
int N = x.size();
// 按位反转
for (int i = 1, j = 0; i < N; i++)
{
//bit = N/2
int bit = N >> 1;
/*
* 我们正在查看j的二进制表示中的每一位。
从左到右,我们检查每一位是否为1。
对于每一个为1的位,我们将其反转为0。
当我们遇到第一个为0的位时,循环终止。
*/
for (; j & bit; bit >>= 1)
{
j ^= bit;
}
//进行异或运算(XOR运算的工作原理是:当两个比较的位相同时,结果是0;当两个比较的位不同时,结果是1。)
j ^= bit;
//当 i >j 表示前面已经替换了位置, i==j,表示位置不用变
if (i < j)
{
std::swap(x[i], x[j]);
}
}
// 预先计算旋转因子
Eigen::VectorXcd w(N >> 1);
//逆变换 = 1;傅里叶变换 = -1;
double imag_i = inv ? 1.0 : -1.0;
std::complex<double> tempW = std::exp(std::complex<double>(0, imag_i * 2 * M_PI / N));
w[0] = 1;
for (int i = 1; i < (N >> 1); ++i)
{
// w[i] = std::polar(1.0, imag_i * 2 * M_PI * i / N);
//w[i] = std::pow(tempW, i);
w[i] = w[i - 1] * tempW;
}
// 迭代FFT
for (int len = 2; len <= N; len <<= 1)
{
int halfLen = len >> 1;
int step = N / len;
for (int i = 0; i < N; i += len)
{
for (int j = 0; j < halfLen; ++j)
{
std::complex<double> u = x[i + j];
std::complex<double> v = x[i + j + halfLen] * w[j * step];
x[i + j] = u + v;
x[i + j + halfLen] = u - v;
}
}
}
//使用逆变换时
if (inv)
{
for (std::complex<double>& a : x) {
a /= N;
}
}
return x;
}
//检查二维数据大小是否为2的幂数,不是则填充为0到2的幂数大小
Eigen::MatrixXd padToPowerOfTwo(const Eigen::MatrixXd& matrix) {
int rows = matrix.rows();
int cols = matrix.cols();
// 确保输入的大小是2的幂
int newRows = 1, newCols = 1;
while (newRows < rows)
{
newRows <<= 1;
}
while (newCols < cols)
{
newCols <<= 1;
}
Eigen::MatrixXd paddedMatrix = Eigen::MatrixXd::Zero(newRows, newCols);
paddedMatrix.block(0, 0, rows, cols) = matrix;
return paddedMatrix;
}
// 离散傅里叶变换 - 二维
Eigen::MatrixXcd FFT2D(const Eigen::MatrixXcd& image, bool inv = false) {
int rows = image.rows();
int cols = image.cols();
Eigen::MatrixXcd result(rows, cols);
for (int i = 0; i < rows; i++) {
Eigen::VectorXcd temp = image.row(i).transpose();
result.row(i) = FFT(temp, inv);
}
for (int j = 0; j < cols; j++) {
Eigen::VectorXcd temp = result.col(j);
result.col(j) = FFT(temp, inv);
}
return result;
}
//创建高频 radius越小,越减少高频的部分,越大,越还原图像
Eigen::MatrixXd highFrequency (const Eigen::MatrixXd & data,int radius)
{
int rows = data.rows();
int cols = data.cols();
// 创建高通滤波器(圆形掩码)
Eigen::MatrixXd mask = Eigen::MatrixXd::Ones(rows, cols);
//中心坐标
int centerRow = rows >> 1;
int centerCol = cols >> 1;
//找到以 radius 大小的矩形范围内
//左边位置
int left = centerCol - radius;
//超过边界 为0
left = left > 0 ? left : 0;
//右边位置
int right = centerCol + radius;
//超过边界 为0
right = right < cols ? right : cols;
//上边位置
int top = centerRow - radius;
//超过边界 为0
top = top > 0 ? top : 0;
//下边位置
int down = centerRow + radius;
//超过边界 为0
down = down < rows ? down : rows;
//在正矩形内画最大的圆
for (int i = top; i < down; ++i)
{
for (int j = left; j < right; ++j)
{
//在图像中心画圆,半径不能超过
double distance = std::sqrt(std::pow(i - centerRow, 2) + std::pow(j - centerCol, 2));
if (distance <= radius)
{
mask(i, j) = 0.0;
}
}
}
return mask;
}
//创建高通滤波器 -
//简单的说,就是靠近频谱图中心的低频部分给舍弃掉,远离频谱图中心的高频部分保留。通常会保留物体的边界。
Eigen::MatrixXd highPassFilter(const Eigen::MatrixXd & image, int radius = 0)
{
int rows = image.rows();
int cols = image.cols();
//大小变为2的幂数
Eigen::MatrixXd data = padToPowerOfTwo(image);
// 计算傅里叶变换
Eigen::MatrixXcd transformed = FFT2D(data);
//获取幅度谱和相位谱
Eigen::MatrixXd amplitude, phase;
getAmplitudeAndPhaseSpectra(transformed, amplitude, phase);
//振幅谱移动到中心(频率平移)
amplitude = fftShift(amplitude);
///
//增强振幅,用于观测 -- 实际运算注释掉
Eigen::MatrixXd amplitude1 = enhanceSpectrumDisplay(amplitude,1);
cv::Mat highP = tMat(amplitude1);
cv::imshow("highPassFilter",highP);
///
//根据radius创建高频掩码
Eigen::MatrixXd mask = highFrequency(amplitude, radius);
amplitude = amplitude.array() * mask.array();
//振幅谱移动到中心(频率平移)反转换
amplitude = fftShift(amplitude);
// 从幅度谱和相位谱重构复数矩阵
reconstructFromAmplitudeAndPhase(amplitude, phase, transformed);
// 计算逆变换
Eigen::MatrixXcd reconstructed = FFT2D(transformed, true);
return reconstructed.real().block(0, 0, rows, cols);
}
//创建低频 radius越小,越还原图像,越大,减少低频的部分,
Eigen::MatrixXd lowFrequency(const Eigen::MatrixXd & data,int radius)
{
int rows = data.rows();
int cols = data.cols();
// 创建低通滤波器(圆形掩码)
Eigen::MatrixXd mask = Eigen::MatrixXd::Zero(rows, cols);
//中心坐标
int centerRow = rows >> 1;
int centerCol = cols >> 1;
//找到以 radius 大小的矩形范围内
//左边位置
int left = centerCol - radius;
//超过边界 为0
left = left > 0 ? left : 0;
//右边位置
int right = centerCol + radius;
//超过边界 为0
right = right < cols ? right : cols;
//上边位置
int top = centerRow - radius;
//超过边界 为0
top = top > 0 ? top : 0;
//下边位置
int down = centerRow + radius;
//超过边界 为0
down = down < rows ? down : rows;
//在正矩形内画最大的圆
for (int i = top; i < down; ++i)
{
for (int j = left; j < right; ++j)
{
//在图像中心画圆,半径不能超过
double distance = std::sqrt(std::pow(i - centerRow, 2) + std::pow(j - centerCol, 2));
if (distance <= radius)
{
mask(i, j) = 1.0;
}
}
}
return mask;
}
//创建低通滤波器 -
//简单的说,就是靠近频谱图中心的低频部分给保留,远离频谱图中心的高频部分给去除掉。但是这会影响图像的清晰度。
Eigen::MatrixXd lowPassFilter(const Eigen::MatrixXd & image, int radius = 0)
{
int rows = image.rows();
int cols = image.cols();
//大小变为2的幂数
Eigen::MatrixXd data = padToPowerOfTwo(image);
// 计算傅里叶变换
Eigen::MatrixXcd transformed = FFT2D(data);
//获取幅度谱和相位谱
Eigen::MatrixXd amplitude, phase;
getAmplitudeAndPhaseSpectra(transformed, amplitude, phase);
//振幅谱移动到中心(频率平移)
amplitude = fftShift(amplitude);
///
// //增强振幅,用于观测 -- 实际运算注释掉
// Eigen::MatrixXd amplitude1 = enhanceSpectrumDisplay(amplitude,1);
// cv::Mat highP = tMat(amplitude1);
// cv::imshow("lowPassFilter",highP);
///
//根据radius创建高频掩码
Eigen::MatrixXd mask = lowFrequency(amplitude, radius);
amplitude = amplitude.array() * mask.array();
//振幅谱移动到中心(频率平移)反转换
amplitude = fftShift(amplitude);
// 从幅度谱和相位谱重构复数矩阵
reconstructFromAmplitudeAndPhase(amplitude, phase, transformed);
// 计算逆变换
Eigen::MatrixXcd reconstructed = FFT2D(transformed, true);
return reconstructed.real().block(0, 0, rows, cols);
}
int main()
{
cv::Mat img = cv::imread("193560523230866.png");
if (img.empty())
{
std::cout << "请确定是否输入正确的图像文件" << std::endl;
}
cv::Mat gray;
cvtColor(img, gray, cv::COLOR_BGR2GRAY);
//图像转换CV_32F储存
gray.convertTo(gray, CV_32F, 1 / 255.0, 0);
//图像太大,用直接计算 耗时太长,缩小比例
//resize(gray, gray, cv::Size(80, 80));
//Mat 转 MatrixXd
Eigen::MatrixXd image = tMatrixXd(gray);
// 记录开始时间
auto start = std::chrono::high_resolution_clock::now();
//低频
Eigen::MatrixXd low = lowPassFilter(image,50);
//高频
Eigen::MatrixXd high = highPassFilter(image, 50);
// 记录结束时间
auto stop = std::chrono::high_resolution_clock::now();
// 计算持续时间
auto duration = std::chrono::duration_cast<std::chrono::microseconds>(stop - start);
qDebug() << "代码运行时长: " << duration.count() << " 微秒" ;
cv::Mat lowP = tMat(low);
//+0.5 增加显示效果
high = high.array() + 0.5;
cv::Mat highP = tMat(high);
cv::imshow("lowP",lowP);
cv::imshow("highP",highP);
return 0;
}
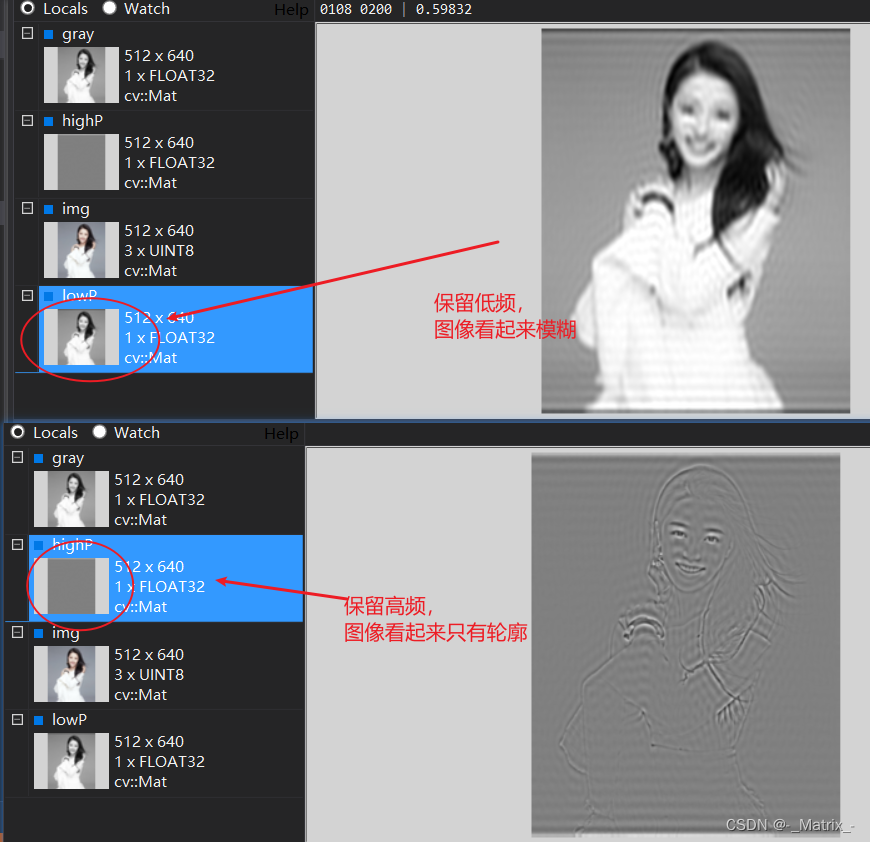
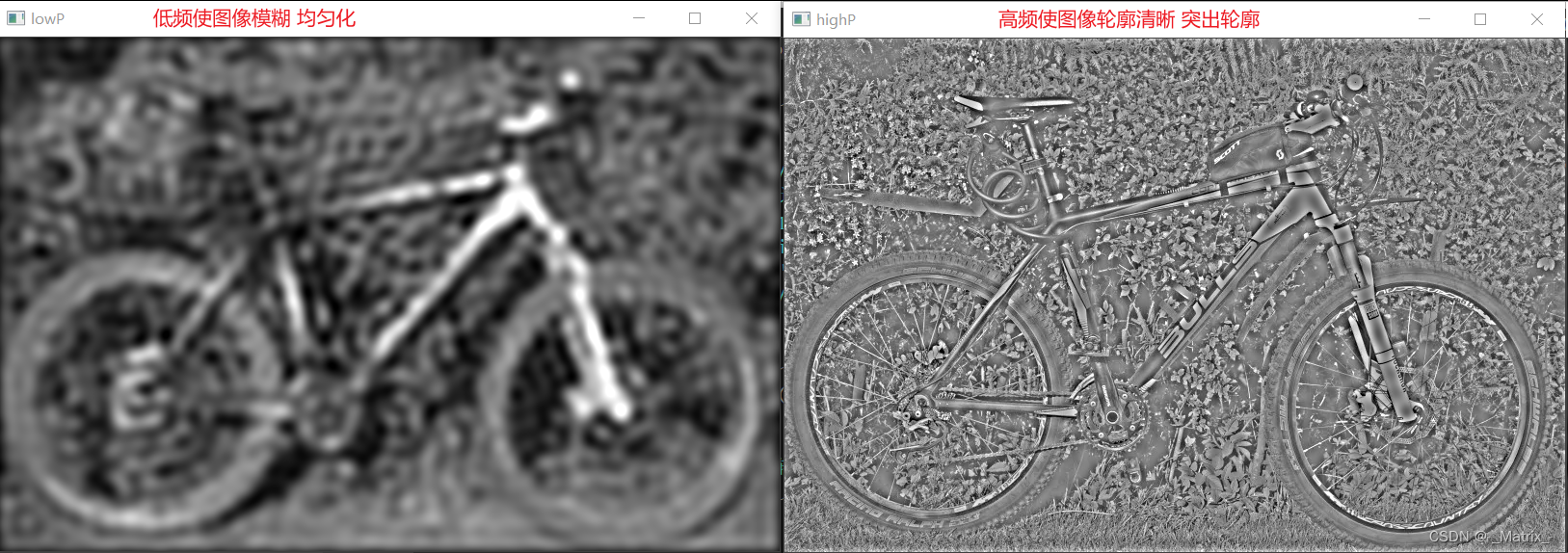
- 振幅增强