1. 题目解析

题目链接：1089. 复写零 - 力扣（Leetcode）

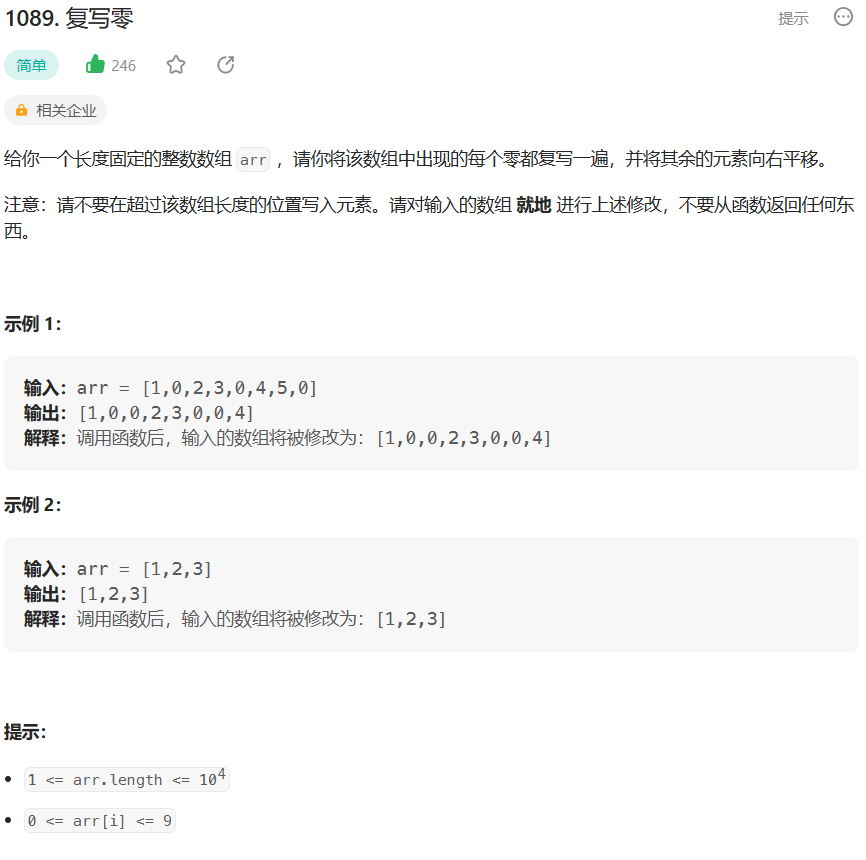
我先来读题，

题目的意思非常的简单，其实就是，

遇到 0 就复制一个写进数组，然后右边的元素就右移一位，

看一眼例子可以很容易理解题意。

2. 算法原理

一般像这种需要移动数组的元素的题目，

也非常常用双指针算法来解题。

这道题如果不使用原地算法，会非常简单，

一个指针遍历原数组，一个指针遍历新数组，

遇到非 0 就直接写进数组，遇到 0 就写两个0进数组即可。

而如果我们想把这个算法优化成原地呢？

我们先从左往右试一下：

看起来并不太行：

会出现全部都复写成0的情况，因为原来的数被修改了，

那我们可以试试从后往前的思路：

我们让cur 指向最后一次写入的位置：

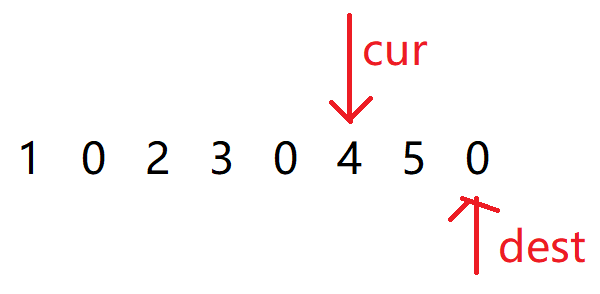
然后模拟双指针的过程：

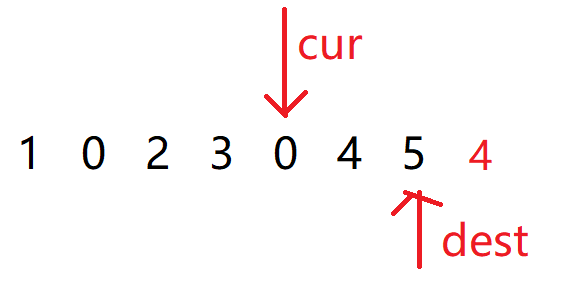
cur遇到0就复写两次：

遇到非 0 就正常写入：

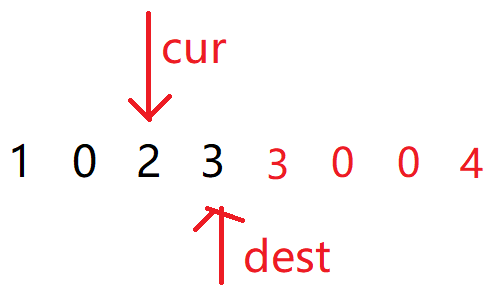
以此类推：

我们发现就成功了，

那现在问题来了，我们怎么得到cur的起始位置，

或者说我们该怎么得到最后一次写入的位置？

我们可以用 cur 和 dest 两个指针来模拟写入的过程，是的，又是双指针：

1. 判断cur位置是 0 还是非0

2. dest根据cur位置的值决定走一步还是走两步

3. 判断dest是否已经走到结尾了

4. 如果没到结尾就cur++，如果已经走到结尾了那cur指向的位置就是最后一次写入的数

不过要小心dest的越界问题，如果走到倒数第二个数的时候，cur走到0，

dest往后走两步就会出现越界的问题。我们到时候让cur后退一步，dest后退两步就行。

3. 代码编写

class Solution {
public:
    void duplicateZeros(vector<int>& arr) {
        int dest = -1, cur = 0, size = arr.size();
        // 找到最后一次写入的位置
        while(cur < size) {
            if(arr[cur]) dest++;
            else dest += 2;
            if(dest >= size - 1) break; //走完了
            cur++;
        }
        // 控制边界
        if(dest == size) { //这种就是最后一步是0，走了两步dest越界的情况
            arr[size - 1] = 0;
            dest -= 2;
            cur--;
        }
        // 从后往前做写入操作
        while(cur >= 0) {
            if(arr[cur]) arr[dest--] = arr[cur--];
            else {
                arr[dest--] = 0;
                arr[dest--] = 0;
                cur--;
            }
        }
    }
};