机器学习---LDA代码

1. 获取投影坐标

import numpy as np


def GetProjectivePoint_2D(point, line):
    a = point[0]
    b = point[1]
    k = line[0]
    t = line[1]

    if   k == 0:      return [a, t]
    elif k == np.inf: return [0, b]
    x = (a+k*b-k*t) / (k*k+1)
    y = k*x + t
    return [x, y]

该函数用于获取一个点到一条直线的投影点的坐标。函数中的参数point表示点的坐标，以[a,b]

的形式表示；参数line表示直线的参数，以[k,t]的形式表示，其中k表示直线的斜率，t表示直线的截

距。函数的返回值为投影点的坐标，以[a',b']的形式表示。

函数的具体实现如下：

从point参数中获取点的横坐标a和纵坐标b，从line参数中获取直线的斜率k和截距t。

若斜率k为0，则直线为水平线，投影点的纵坐标为直线的截距t，横坐标不变，返回投影点的坐标

[a,t]。

若斜率k为正无穷大，则直线为垂直线，投影点的横坐标为0，纵坐标不变，返回投影点的坐标

[0,b]。

计算投影点的横坐标x，公式为x = (a + kb - kt) / (k*k + 1)。

通过直线的方程y = k*x + t计算投影点的纵坐标y。

返回投影点的坐标[x, y]。

注：该函数使用了numpy库中的inf表示正无穷大。

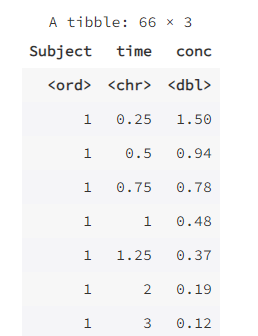
2. 绘制散点图

X = dataset[:,1:3]
y = dataset[:,3]
print(X,y)
# draw scatter diagram to show the raw data
f1 = plt.figure(1)       
plt.title('watermelon_3a')  
plt.xlabel('density')  
plt.ylabel('ratio_sugar')  
print(X[y == 0,0], X[y == 0,1])
plt.scatter(X[y == 0,0], X[y == 0,1], marker = 'o', color = 'k', s=100, label = 'bad')
plt.scatter(X[y == 1,0], X[y == 1,1], marker = 'o', color = 'g', s=100, label = 'good')
plt.legend(loc = 'upper right')  
plt.show()

在Python中，布尔索引操作可以直接应用在数组对象上。

当我们执行y == 0时，它会生成一个布尔数组，其中的每个元素都是y数组对应位置上的值是

否等于0的结果。例如，如果y数组的某个元素为1，则对应的布尔数组元素为False；如果y数组的

某个元素为0，则对应的布尔数组元素为True。然后，我们可以将这个布尔数组作为索引应用在另

一个数组上，以获取符合条件的元素。对于二维数组来说，第一个索引表示行，第二个索引表示

列。因此，X[y == 0, 0]表示获取X数组中满足y数组对应位置上的值等于0的行索引的第0列的元

素。

3. LDA进行分类

from sklearn import model_selection
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn import metrics
import matplotlib.pyplot as plt

# generalization of train and test set
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size=0.5, random_state=0)

# model fitting
lda_model = LinearDiscriminantAnalysis(solver='lsqr', shrinkage=None).fit(X_train, y_train)

# model validation
y_pred = lda_model.predict(X_test)

# summarize the fit of the model
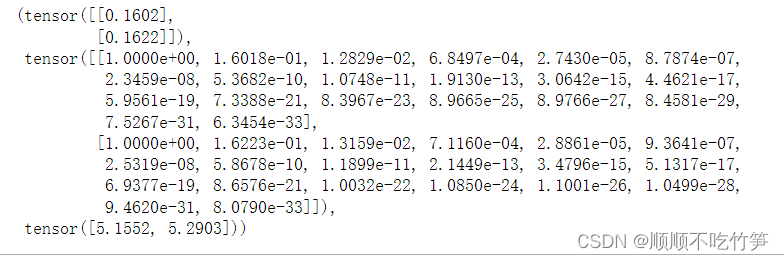
print(metrics.confusion_matrix(y_test, y_pred))
print(metrics.classification_report(y_test, y_pred))

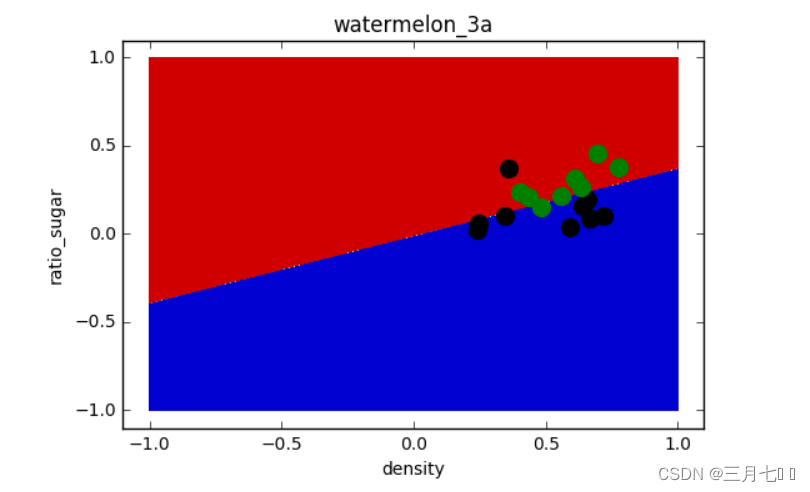
# draw the classfier decision boundary
f2 = plt.figure(2) 
h = 0.001
# x0_min, x0_max = X[:, 0].min()-0.1, X[:, 0].max()+0.1
# x1_min, x1_max = X[:, 1].min()-0.1, X[:, 1].max()+0.1

x0, x1 = np.meshgrid(np.arange(-1, 1, h),
                     np.arange(-1, 1, h))

# x0, x1 = np.meshgrid(np.arange(x0_min, x0_max, h),
#                      np.arange(x1_min, x1_max, h))

z = lda_model.predict(np.c_[x0.ravel(), x1.ravel()]) 

# Put the result into a color plot
z = z.reshape(x0.shape)
plt.contourf(x0, x1, z)

# Plot also the training pointsplt.title('watermelon_3a')  
plt.title('watermelon_3a')  
plt.xlabel('density')  
plt.ylabel('ratio_sugar')  
plt.scatter(X[y == 0,0], X[y == 0,1], marker = 'o', color = 'k', s=100, label = 'bad')
plt.scatter(X[y == 1,0], X[y == 1,1], marker = 'o', color = 'g', s=100, label = 'good')
plt.show()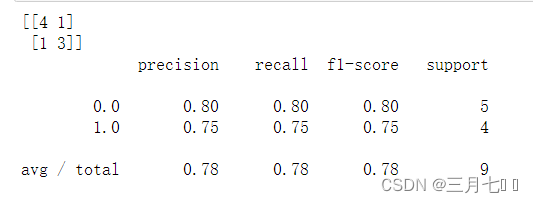

model_selection模块中的train_test_split函数。该函数的作用是将数据集划分为训练集和测试

集，并返回划分后的数据。

具体而言，train_test_split函数的参数包括：

X：要划分的特征数据集

y：要划分的目标变量数据集

test_size：测试集的大小，可以是一个浮点数（表示比例）或一个整数（表示样本数量）

random_state：随机种子，用于控制划分的随机性

函数的返回值是四个数组：

X_train：训练集的特征数据

X_test：测试集的特征数据

y_train：训练集的目标变量数据

y_test：测试集的目标变量数

LinearDiscriminantAnalysis类的一些常用参数及其意义：

solver：求解器的选择，用于计算LDA模型的参数。可选的求解器包括：'svd'：奇异值分解

（Singular Value Decomposition），适用于任意维度的数据。'lsqr'：最小二乘法（Least

Squares），适用于高维数据。'eigen'：特征值分解（Eigenvalue Decomposition），适用于小样

本数据。

shrinkage：收缩参数的选择，用于控制LDA模型的收缩程度。可选的收缩参数包括：None：不应

用收缩，使用经典的LDA方法。'auto'：自动选择收缩参数，根据数据的特征自动确定收缩程度。

浮点数：手动指定收缩参数的值，值越大表示收缩程度越高。

n_components：降维后的特征维度数目。默认值为None，表示不进行降维。

priors：类别的先验概率。如果指定了先验概率，则LDA模型将使用这些先验概率进行计算。

store_covariance：是否存储类别的协方差矩阵。默认为False，表示不存储协方差矩阵。如果设置

为True，则可以通过covariance_属性访问类别的协方差矩阵。

lda_model.predict(X_test)的作用是使用已经训练好的LDA模型 lda_model 对测试集数据

X_test 进行预测，返回预测的目标变量值。

metrics.confusion_matrix(y_test, y_pred)的作用是计算预测结果与真实标签之间的混淆矩阵。

该函数的参数包括：y_test：测试集的真实标签，是一个一维数组或列表。y_pred：模型对测试集

的预测结果，也是一个一维数组或列表。

metrics.classification_report(y_test, y_pred)的作用是生成分类模型的分类报告，其中包含了

一些评估指标，用于评估模型在测试集上的性能。分类报告提供了以下指标：准确率

（Precision）：预测为正例的样本中，实际为正例的比例。召回率（Recall）：实际为正例的样本

中，被正确预测为正例的比例。F1分数（F1-Score）：综合考虑了准确率和召回率的指标，是二

者的调和平均值。支持数（Support）：每个类别在测试集中的样本数量。

np.arange(-1, 1, h)：指定了生成一维数组的起始值、结束值和步长。在这里，起始值为-1，结

束值为1，步长为h。np.meshgrid函数的作用是将这两个一维数组转换为两个二维数组 x0 和 x1，

其中 x0 的每一行都是 np.arange(-1, 1, h)，而 x1 的每一列都是 np.arange(-1, 1, h)。

np.ravel(arr) 其中包含原始数组中的所有元素，按照从左到右、从上到下的顺序排列。np.c_

[x0.ravel(), x1.ravel()] 将 x0 和 x1 两个二维数组展平，并按列连接成一个新的二维数组。这样得到

的数组表示了二维网格中的所有点的坐标。

这样做预测的目的是为了可视化分类器的决策边界。通过在二维网格中生成一组坐标点，并对

这些点进行预测，可以得到每个点的预测类别。然后，可以使用这些预测结果来绘制决策边界。决

策边界是分类器在特征空间中将不同类别分开的边界。通过绘制决策边界，可以直观地了解分类器

对不同区域的分类结果。

通过对二维网格中的点进行预测，得到了每个点的预测类别 z。然后，使用 plt.contourf() 函数

将这些预测结果绘制成一个颜色图，其中不同的颜色表示不同的类别。

4. 计算参数w

u = []  
for i in range(2): # two class
    u.append(np.mean(X[y==i], axis=0))  # column mean

# 2-nd. computing the within-class scatter matrix, refer on book (3.33)
m,n = np.shape(X)
Sw = np.zeros((n,n))
for i in range(m):
    x_tmp = X[i].reshape(n,1)  # row -> cloumn vector
    if y[i] == 0: u_tmp = u[0].reshape(n,1)
    if y[i] == 1: u_tmp = u[1].reshape(n,1)
    Sw += np.dot( x_tmp - u_tmp, (x_tmp - u_tmp).T )

Sw = np.mat(Sw)
U, sigma, V= np.linalg.svd(Sw) 

Sw_inv = V.T * np.linalg.inv(np.diag(sigma)) * U.T
# 3-th. computing the parameter w, refer on book (3.39)
w = np.dot( Sw_inv, (u[0] - u[1]).reshape(n,1) )  # here we use a**-1 to get the inverse of a ndarray

print(w)

这段代码是用于计算线性判别分析（Linear Discriminant Analysis）中的参数w的。下面是代码的

解释：

首先，创建一个空列表u，用于存储每个类别的均值向量。

然后，通过循环遍历每个类别，计算每个类别的均值向量，并将其添加到列表u中。

接下来，计算类内散布矩阵（within-class scatter matrix）。首先，初始化一个全零矩阵Sw，其大

小为(n,n)，其中n是特征向量的维度。然后，通过循环遍历每个样本，将样本向量转置为列向量，

并根据其所属的类别选择相应的均值向量。然后，计算每个样本向量与其所属类别的均值向量之间

的差，并将其乘以其转置，最后将结果累加到Sw中。

将Sw转换为矩阵类型。

对Sw进行奇异值分解（Singular Value Decomposition，SVD），得到矩阵U、sigma和V。

计算Sw的逆矩阵Sw_inv，其中V.T表示V的转置，np.linalg.inv(np.diag(sigma))表示sigma的逆矩阵

的对角矩阵。

最后，计算参数w，通过将Sw_inv与类别0的均值向量u[0]与类别1的均值向量u[1]之间的差相乘得

到。这里使用了**-1来获取ndarray的逆矩阵。

5. 绘制二维散点图和LDA结果

f3 = plt.figure(3)
plt.xlim( -0.2, 1 )
plt.ylim( -0.5, 0.7 )

p0_x0 = -X[:, 0].max()
p0_x1 = ( w[1,0] / w[0,0] ) * p0_x0
p1_x0 = X[:, 0].max()
p1_x1 = ( w[1,0] / w[0,0] ) * p1_x0

plt.title('watermelon_3a - LDA')  
plt.xlabel('density')  
plt.ylabel('ratio_sugar')  
plt.scatter(X[y == 0,0], X[y == 0,1], marker = 'o', color = 'k', s=10, label = 'bad')
plt.scatter(X[y == 1,0], X[y == 1,1], marker = 'o', color = 'g', s=10, label = 'good')
plt.legend(loc = 'upper right')  

plt.plot([p0_x0, p1_x0], [p0_x1, p1_x1])

# draw projective point on the line


m,n = np.shape(X)
for i in range(m):
    x_p = GetProjectivePoint_2D( [X[i,0], X[i,1]], [w[1,0] / w[0,0] , 0] ) 
    if y[i] == 0: 
        plt.plot(x_p[0], x_p[1], 'ko', markersize = 5)
    if y[i] == 1: 
        plt.plot(x_p[0], x_p[1], 'go', markersize = 5)   
    plt.plot([ x_p[0], X[i,0]], [x_p[1], X[i,1] ], 'c--', linewidth = 0.3)

plt.show()

创建一个名为f3的图形对象。设置x轴的显示范围为-0.2到1。设置y轴的显示范围为-0.5到0.7。

计算类别0中第一维特征的最大值的相反数。根据权重计算类别0中第二维特征的值。

计算类别1中第一维特征的最大值。根据权重计算类别1中第二维特征的值。

p0_x0表示X轴上的最小值，而p0_x1表示通过线性模型计算得出的对应于p0_x0的预测值。同

样地，p1_x0表示X轴上的最大值，而p1_x1表示通过线性模型计算得出的对应于p1_x0的预测值。

这样做的目的是为了可视化线性模型在二维空间中的表现。通过计算出这两个点，我们可以在X轴

上绘制一条直线，该直线表示线性模型的决策边界。这样可以更好地理解线性模型对输入数据的分

类或回归能力。

设置图形的标题为'watermelon_3a - LDA'。设置x轴的标签为'density'。

设置y轴的标签为'ratio_sugar'。绘制类别0的散点图，使用黑色圆点表示，大小为10，标签

为'bad'。绘制类别1的散点图，使用绿色圆点表示，大小为10，标签为'good'。

在图形的右上角显示图例。绘制连接类别0和类别1投影点的直线。

获取数据集X的形状，m为样本数，n为特征数。遍历每个样本。

x_p = GetProjectivePoint_2D([X[i, 0], X[i, 1]], [w[1, 0] / w[0, 0], 0]): 计算样本点在直线上的投

影点。函数 GetProjectivePoint_2D 的参数有两个：[X[i, 0], X[i, 1]]：这是一个包含两个元素的列

表，表示二维平面上的一个点的坐标。X[i, 0] 表示点的 x 坐标，X[i, 1] 表示点的 y 坐标。[w[1, 0] /

w[0, 0], 0]：这是一个包含两个元素的列表，表示一个向量的坐标。w[1, 0] / w[0, 0] 表示向量的 x

分量，0 表示向量的 y 分量。函数的作用是将给定的二维平面上的点 [X[i, 0], X[i, 1]] 投影到由向量

[w[1, 0] / w[0, 0], 0] 所定义的直线上，并返回投影点的坐标。

如果样本属于类别0。绘制类别0的投影点，使用黑色圆点表示，大小为5。如果样本属于类别

1。绘制类别1的投影点，使用绿色圆点表示，大小为5。绘制从样本点到投影点的虚线，使用青色

虚线表示，线宽为0.3。

6. LDA示例

X = np.delete(X, 14, 0)
y = np.delete(y, 14, 0)

u = []  
for i in range(2): # two class
    u.append(np.mean(X[y==i], axis=0))  # column mean

# 2-nd. computing the within-class scatter matrix, refer on book (3.33)
m,n = np.shape(X)
Sw = np.zeros((n,n))
for i in range(m):
    x_tmp = X[i].reshape(n,1)  # row -> cloumn vector
    if y[i] == 0: u_tmp = u[0].reshape(n,1)
    if y[i] == 1: u_tmp = u[1].reshape(n,1)
    Sw += np.dot( x_tmp - u_tmp, (x_tmp - u_tmp).T )

Sw = np.mat(Sw)
U, sigma, V= np.linalg.svd(Sw) 

Sw_inv = V.T * np.linalg.inv(np.diag(sigma)) * U.T
# 3-th. computing the parameter w, refer on book (3.39)
w = np.dot( Sw_inv, (u[0] - u[1]).reshape(n,1) )  # here we use a**-1 to get the inverse of a ndarray

print(w)

# 4-th draw the LDA line in scatter figure

# f2 = plt.figure(2)
f4 = plt.figure(4)
plt.xlim( -0.2, 1 )
plt.ylim( -0.5, 0.7 )

p0_x0 = -X[:, 0].max()
p0_x1 = ( w[1,0] / w[0,0] ) * p0_x0
p1_x0 = X[:, 0].max()
p1_x1 = ( w[1,0] / w[0,0] ) * p1_x0

plt.title('watermelon_3a - LDA')  
plt.xlabel('density')  
plt.ylabel('ratio_sugar')  
plt.scatter(X[y == 0,0], X[y == 0,1], marker = 'o', color = 'k', s=10, label = 'bad')
plt.scatter(X[y == 1,0], X[y == 1,1], marker = 'o', color = 'g', s=10, label = 'good')
plt.legend(loc = 'upper right')  

plt.plot([p0_x0, p1_x0], [p0_x1, p1_x1])

# draw projective point on the line


m,n = np.shape(X)
for i in range(m):
    x_p = GetProjectivePoint_2D( [X[i,0], X[i,1]], [w[1,0] / w[0,0] , 0] ) 
    if y[i] == 0: 
        plt.plot(x_p[0], x_p[1], 'ko', markersize = 5)
    if y[i] == 1: 
        plt.plot(x_p[0], x_p[1], 'go', markersize = 5)   
    plt.plot([ x_p[0], X[i,0]], [x_p[1], X[i,1] ], 'c--', linewidth = 0.3)

plt.show()