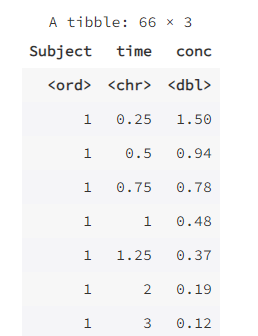
题目：一个3阶的数字矩阵如下：

1 2 3

8 9 4

7 6 5

现在给定数字n(1<n≤20)，输出n阶数字矩阵。

思路：

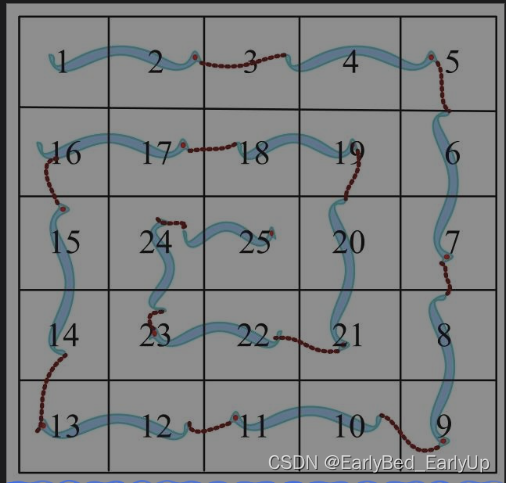
放出一条好玩的贪吃蛇，按照右下左上的顺序吃蛋糕，一边吃蛋糕，一边拉数字；多吃一个蛋糕，拉出的数字多1，直到把所有的蛋糕吃完。

因为贪吃蛇出动按照右、下、左、上4个方向，因此先定义一个按右下左上方向的偏移数组。

定义了偏移数组后，就可以从左上角开始，先向右走，只要有蛋糕或未到边界就继续前进，否则选择下一个方向（右下左上顺序），一直走下去，直到拉出的数字达到最大值n2，算法停止。

因为吃了蛋糕后，这个方格就变成了一个大于零的数字，因此可以设置为0时有蛋糕，否则没有蛋糕。初始状态全部为0。

本题因为不可以超出四周边界，因此采用四周封锁。设置一个无法行进的数值，即可达到封锁目的。在第0行和第n+1行设置数字-1，第0列和第n+1列设置数字-1，标识四周无法行进。

做了封锁之后，再也不用担心小贪吃蛇跑出边界了，它只需要按照右下左上的方向，只吃有蛋糕的格子（数值为0）就可以了。

 

#include<iostream>
#include<algorithm>
using namespace std;

typedef struct{
	int x;
	int y;
} Position;

int m[30][30];			//存地图 
Position here, next;	//当前位置，下一位置 
Position DIR[4] ={0,1,1,0,0,-1,-1,0};//右下左上方向数组 

void Init(int n)
{
	for(int i=1; i<=n; ++i)
		for(int j=1; j<=n; ++j)
			m[i][j] =0;			//地图初始化为0 
			
	for(int i=0; i<=n+1; ++i)
		m[i][0] =m[i][n+1] =-1;	//左右围墙 
		
	for(int j=0; j<=n+1; ++j)
		m[0][j] =m[n+1][j] =-1; //上下围墙 
}

void Solve(int n)
{
	m[1][1] =1;					//第一个数 
	here.x =here.y =1;			//初始化位置 
	int dirIndex =0, num =1; 	//偏移下标， 总数
	
	while(num<n*n){
		
		next.x =here.x + DIR[dirIndex].x;
		next.y =here.y + DIR[dirIndex].y;
		
		if(m[next.x][next.y]==0){
			m[next.x][next.y] =++num;	//满足条件则更新地图 
			here =next;					//继续走 
		}
		else{
			dirIndex =(dirIndex+1)%4;	//碰到围墙换方向 
		} 
	} 
}

int main()
{
	int n =0;
	cin>> n;
	
	Init(n);
	Solve(n);
	
	for(int i=1; i<=n; ++i){
		for(int j=1; j<=n; ++j)
			cout<< "\t"<< m[i][j];
		cout<< endl;
	}	
	return 0;
}

                                                                                                       来源：《趣学数据结构》陈小玉