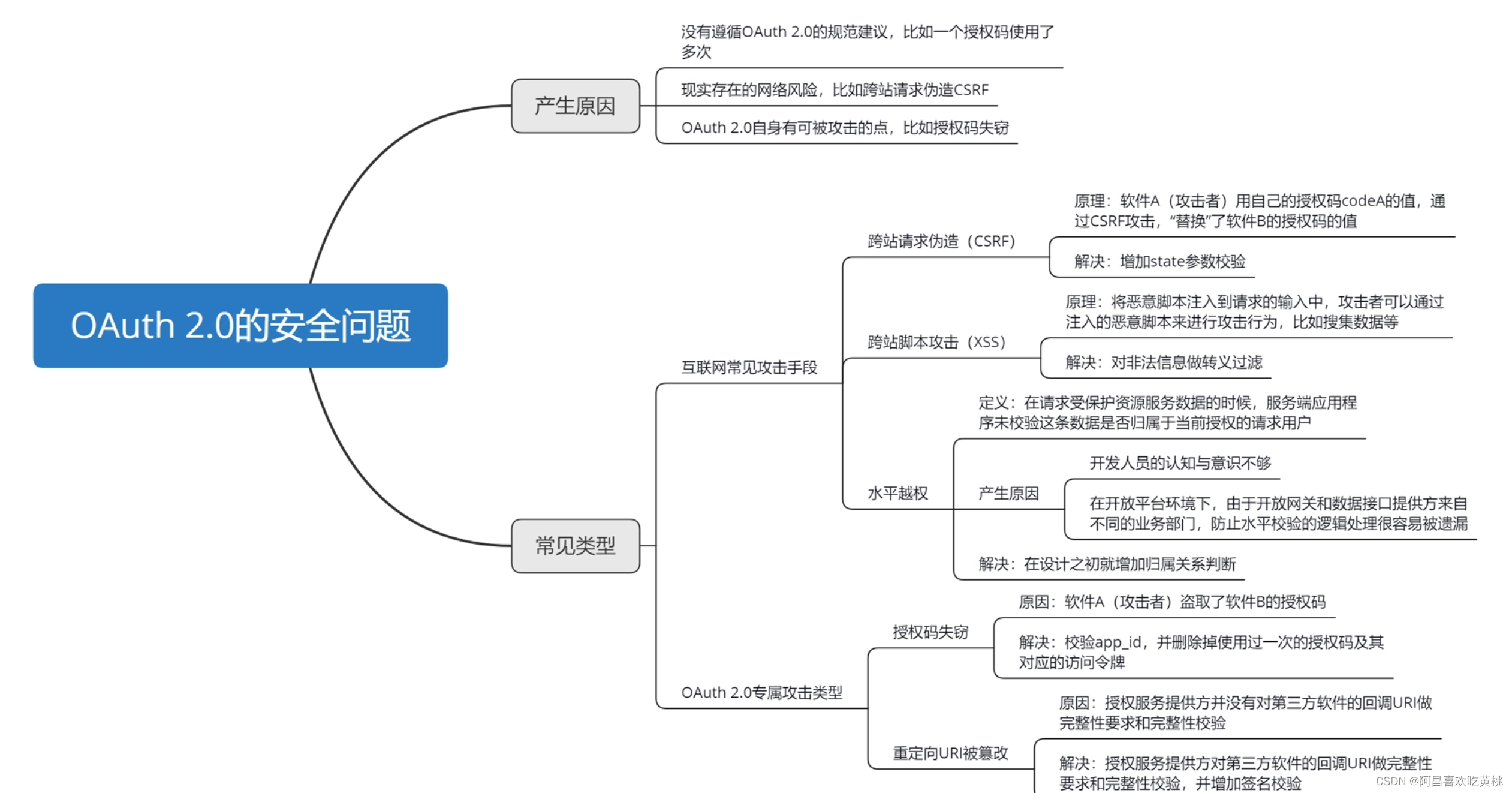
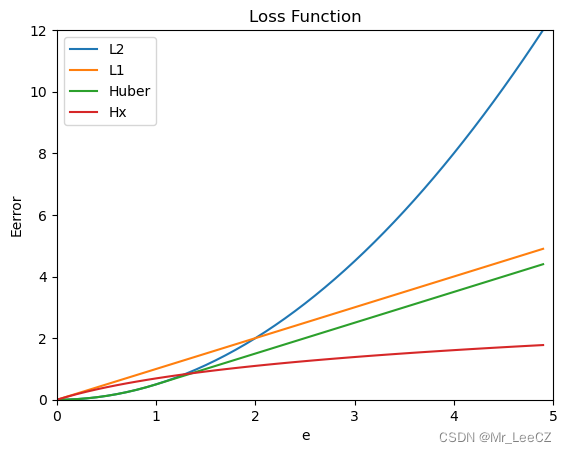
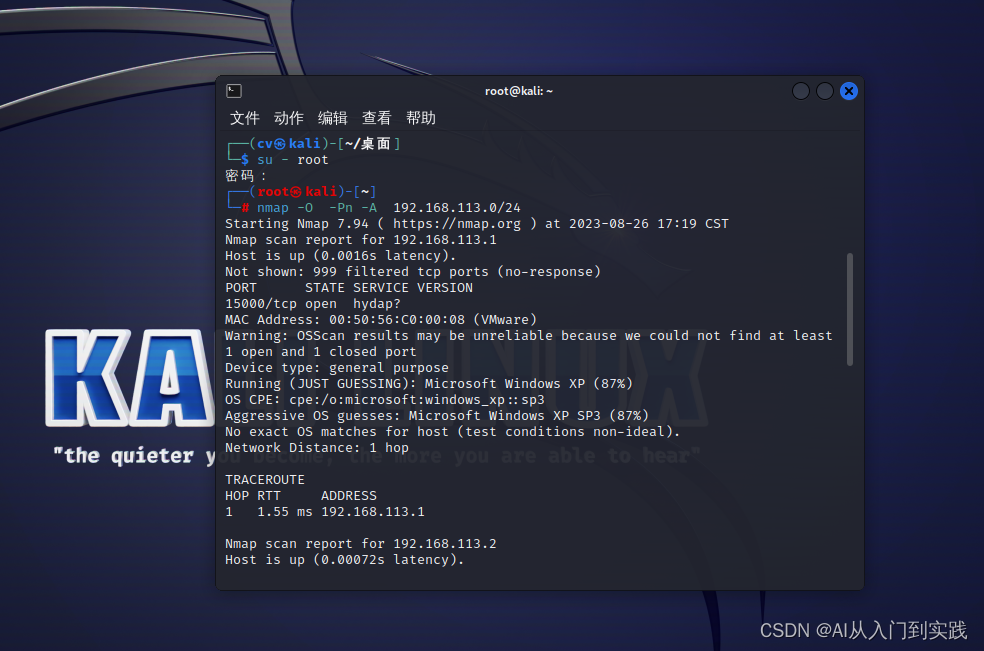
知识:
顶点,边 | 权,度数
1.图的种类:
有向图 | 无向图
有环 | 无环
联通性
基础1:图的存储(主要是邻接矩阵和邻接表)
例一:B3643 图的存储 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
#include <iostream>
using namespace std;
int n, m, d[1010];
bool edges[1010][1010];
int main()
{
cin >> n >> m;
for(int i = 1; i <= m; i ++ )
{
int u, v;
cin >> u >> v;
edges[u][v] = true;
edges[v][u] = true;
}
for(int i = 1; i <= n; i ++ )
{
for(int j = 1; j <= n; j ++ )
{
if(edges[i][j])
{
cout << "1 ";
d[i] ++;
}
else cout << "0 ";
}
cout << endl;
}
for(int i = 1; i <= n; i ++ )
{
cout << d[i] << ' ';
for(int j = 1; j <= n; j ++ )
{
if(edges[i][j]) cout << j << ' ';
}
cout << endl;
}
return 0;
}例二:B3613 图的存储与出边的排序 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
该代码须加上快读快写
#include <iostream>
#include <set>
using namespace std;
const int N = 5e5 + 10;
int n, m;
set<int> s[N];
int main()
{
int t;
cin >> t;
while(t -- )
{
cin >> n >> m;
for(int i = 0; i < m; i ++ )
{
int a, b;
cin >> a >> b;
s[a].insert(b);
}
int j = 0;
for(int i = 1; i <= n; i ++ )
{
for(auto it = s[i].begin(); it != s[i].end(); it ++ )
cout << *it << ' ';
cout << endl;
}
}
return 0;
}图的遍历:通常是bfs()、dfs()
复习一下模板活动 - AcWing 活动 - AcWing
例一:P3916 图的遍历 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
因为是找最大值dfs,用了反向建边提高效率,用一个大值去标记多个小值
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e5 + 10, M = 2 * N;
int n, m;
int e[N], ne[N], h[N], idx;
int res[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u, int maxn)
{
res[u] = max(maxn, res[u]);
for(int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if(!res[j]) dfs(j, maxn);
}
}
int main()
{
cin >> n >> m;
memset(h, -1, sizeof h);
while(m -- )
{
int u, v;
cin >> u >> v;
add(v, u);
}
for(int i = n; i >= 1; i -- )
{
//反向建边+遍历 有利于找最大值的效率
// 如果是第一次被遍历到一定找到了遍历最大的值
//已经被标记过最大值的说明他们下边的最大值也被标记过了
if(res[i]) continue;
dfs(i, i);
}
for(int i = 1; i <= n; i ++ )
{
cout << res[i] << ' ';
}
return 0;
}例二:活动 - AcWing 图的层次
肯定要用bfs啦
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 1e5 + 10;
int h[N], e[N], ne[N], idx;
int d[N];
int n,m;
queue<int> q;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
int bfs()
{
memset(d, -1, sizeof d);
d[1] = 0;
q.push(1);
while(q.size())
{
auto t = q.front();
q.pop();
for(int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if(d[j] == -1)
{
d[j] = d[t] + 1;
q.push(j);
}
}
}
return d[n];
}
int main(){
cin >> n >> m;
memset(h, -1, sizeof h);
for(int i = 0; i < m; i++ )
{
int a, b;
cin >> a >> b;
add(a, b);
}
cout << bfs() << endl;
return 0;
}例三:P5318 【深基18.例3】查找文献 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
分别用dfs和bfs输出一遍。唯一的难点在于怎么做到 "如果有很多篇文章可以参阅,请先看编号较小的那篇(因此你可能需要先排序)。" 问题不大,排个序就行。
注意用邻接表存图(s存边先处理一下,即排序) 然后处理e[i][]表示i点连接的点
然后就是喜闻乐见的dfs递归一下,bfs一下
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 1e5 + 10;
struct edges
{
int a, b;
};
vector<int> e[N]; // e是邻接表,用来遍历
vector<edges> s; // 用来存边
int n, m;
bool st1[N], st2[N];
queue<int> q;
bool cmp(edges x, edges y)
{
//按照每条边终点从小到大排,终点相同的起点按从小到大排
if(x.b == y.b)
return x.a < y.a;
else
return x.b < y.b;
}
void bfs()
{
q.push(1);
st2[1] = true;
cout << '1' << ' ';
while(q.size())
{
int t = q.front();
q.pop();
for(int i = 0; i < e[t].size(); i ++ )
{
int j = s[e[t][i]].b;
if(!st2[j])
{
st2[j] = true;
cout << j << ' ';
q.push(j);
}
}
}
}
void dfs(int u)
{
st1[u] = true;
cout << u << ' ';
for(int i = 0; i < e[u].size(); i ++ )
{
int j = s[e[u][i]].b;
if(!st1[j]) dfs(j);
}
}
int main()
{
cin >> n >> m;
for(int i = 0; i < m; i ++ )
{
int a, b;
cin >> a >> b;
s.push_back((edges){a, b});
}
sort(s.begin(), s.end(), cmp);
//m条边放到e中
for(int i = 0; i < m; i ++ )
{
e[s[i].a].push_back(i); // e存某个点到其他点的边的编号
}
// for(int i = 0; i < m; i ++ )
// {
// cout << s[i].a << ':' << s[i].b << endl;
// }
dfs(1);
puts("");
bfs();
return 0;
}