数学基础、算法与编程

1. BAP 技能

BAP 技能是指基础(Basic)、算法(Algorithm)和编程(Programm)三种基本技能的深度融合。理工科以数学、算法与编程为根基，这三个相辅相成又各有区别。

（1）数学以线性代数为主要研究工具和部分微积分技术为手段，来实现优化的目标。
（2）算法是应用数学和各类数据分析方法的灵魂，搭建了数学与应用领域的之间的桥梁，通常是一种真实解的逼近过程，其中主要涉及到矩阵的运算。
（3）编程泛指一切的计算机语言，通过循环迭代的方式编制出计算过程，如Matlab、Python、C++等，其中会有众多的库可以调用，如scikit-learn、CVX优化库、OpenCV图像处理库等等。

注意：算法和编程是两个严格区分的领域，算法需要深厚的数学功底，编程需要的是简单逻辑。

2. 传统算法

一类常见的算法是误差项 $f(\boldsymbol{x},\boldsymbol{w})$ 和复杂度测度项 $g(\boldsymbol{w})$ 的折衷，形如

$\min_{\boldsymbol{w}}\;f(\boldsymbol{x},\boldsymbol{w})+g(\boldsymbol{w})$

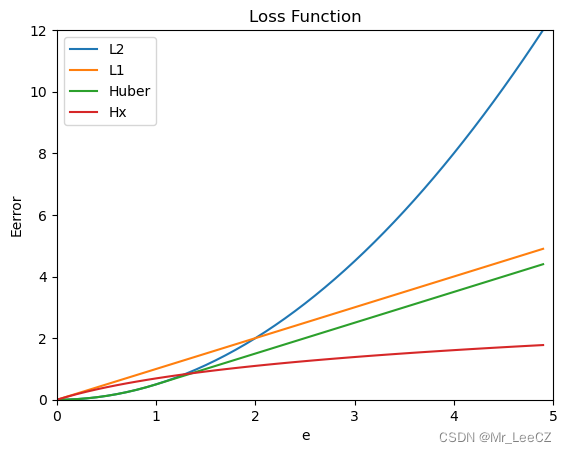
常见的误差项，又称损失函数有以下几种（以回归问题为例）

平方损失

$f(\boldsymbol{x},\boldsymbol{w})=\Vert X\boldsymbol{w}-\boldsymbol{b}\Vert_2^2=\sum_i(w_ix_i-b_i)^2$

绝对值损失

$f(\boldsymbol{x},\boldsymbol{w})=\Vert X\boldsymbol{w}-\boldsymbol{b}\Vert_1=\sum_i\Big\vert b_i-w_ix_i\Big\vert$

Hubber 损失

$\text{Huber}=\left\{ \begin{array}{lcl} \frac{1}{2}e_i^2 & & \vert e_i\vert<\delta\\ \delta\vert e_i\vert -\frac{1}{2}\delta^2 & & \text{Otherwise} \end{array} \right.$

# huber 损失
def huber(e, delta):
    loss = np.where(np.abs(e) < delta , 0.5*(e**2), delta*np.abs(e) - 0.5*(delta**2))
    return loss

import numpy as np
import matplotlib.pyplot as plt

e = np.arange(0,5,0.1)
z1 = 0.5*e**2
z2 = np.abs(e)
z3 = huber(e,1)
z4 = np.log(1+np.abs(e))

plt.plot(e,z1,label='L2')
plt.plot(e,z2,label='L1')
plt.plot(e,z3,label='Huber')
plt.plot(e,z4,label='Hx')
plt.title('Loss Function')
plt.axis([0,5,0,12])
plt.legend()
plt.xlabel('e')
plt.ylabel('Eerror')
plt.show()