文章目录
- 引言
- 一、线性方程组的基本概念与表达形式
- 二、线性方程组解的基本定理
- 三、线性方程组解的结构
- 写在最后
引言
继向量的学习后,一鼓作气,把线性方程组也解决了去。O.O
一、线性方程组的基本概念与表达形式
方程组
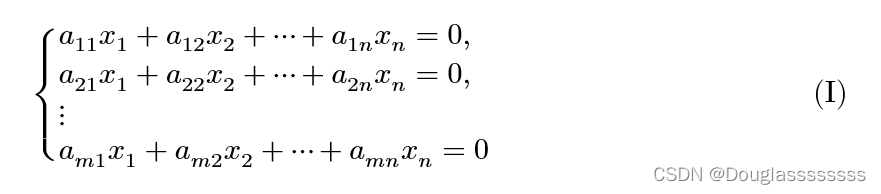
称为
n
n
n 元齐次线性方程组。
方程组
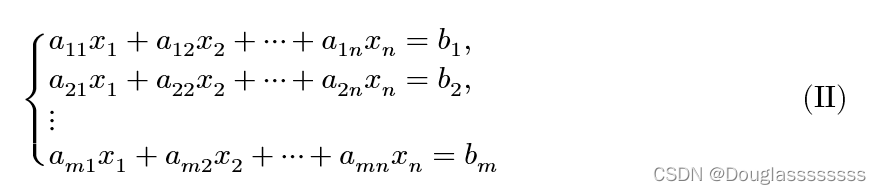
称为
n
n
n 元非齐次线性方程组。
方程组(I)又称为方程组(II)对应的齐次线性方程组或导出方程组。
方程组(I)和方程组(II)分别称为齐次线性方程组和非齐次线性方程组的基本形式。
令 α 1 = ( a 11 , a 21 , … , a m 1 ) T , α 2 = ( a 12 , a 22 , … , a m 2 ) T , … , α n = ( a 1 n , a 2 n , … , a m n ) T , b = ( b 1 , b 2 , … , b m ) T \alpha_1=(a_{11},a_{21},\dots,a_{m1})^T,\alpha_2=(a_{12},a_{22},\dots,a_{m2})^T,\dots,\alpha_n=(a_{1n},a_{2n},\dots,a_{mn})^T,b=(b_{1},b_{2},\dots,b_{m})^T α1=(a11,a21,…,am1)T,α2=(a12,a22,…,am2)T,…,αn=(a1n,a2n,…,amn)T,b=(b1,b2,…,bm)T ,则方程组(I)(II)可表示为如下向量形式: x 1 α 1 + x 2 α 2 + ⋯ + x n α n = 0 ( 1.1 ) x_1\alpha_1+x_2\alpha_2+\dots+x_n\alpha_n=0 (1.1) x1α1+x2α2+⋯+xnαn=0(1.1) x 1 α 1 + x 2 α 2 + ⋯ + x n α n = b ( 2.1 ) x_1\alpha_1+x_2\alpha_2+\dots+x_n\alpha_n=b (2.1) x1α1+x2α2+⋯+xnαn=b(2.1)
令
X
=
(
x
1
,
x
2
,
…
,
x
n
)
T
X=(x_1,x_2,\dots,x_n)^T
X=(x1,x2,…,xn)T ,矩阵
A
=
[
α
1
,
α
2
,
…
,
α
n
]
A=[\alpha_1,\alpha_2,\dots,\alpha_n]
A=[α1,α2,…,αn] ,即

则方程组(I)(II)可表示为如下矩阵形式:
A
X
=
0
(
1.2
)
AX=0(1.2)
AX=0(1.2)
A
X
=
b
(
2.2
)
AX=b(2.2)
AX=b(2.2)
二、线性方程组解的基本定理
其实就是前面我们在学向量时就已经总结过的,矩阵、向量和线性方程组解的关系,传送门。
- 齐次方程组只有零解 ⇔ \Leftrightarrow ⇔ 向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性无关 ⇔ \Leftrightarrow ⇔ r ( A ) = n . r(A)=n. r(A)=n.
- 齐次方程组有非零解 ⇔ \Leftrightarrow ⇔ 向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性相关 ⇔ \Leftrightarrow ⇔ r ( A ) < n . r(A)<n. r(A)<n.
特别地,如果系数矩阵 A A A 为 n n n 阶方阵,还有以下结论:
- 齐次方程组只有零解 ⇔ \Leftrightarrow ⇔ ∣ A ∣ ≠ 0. |A| \ne 0. ∣A∣=0.
- 齐次方程组有非零解 ⇔ \Leftrightarrow ⇔ ∣ A ∣ = 0. |A| = 0. ∣A∣=0.
对于非齐次方程组解的情况,我们可对有解的情况进一步讨论。
- 非齐次方程组有解
⇔
\Leftrightarrow
⇔
r
(
A
‾
)
=
r
(
A
)
.
r(\overline{A})=r(A).
r(A)=r(A).
- 非齐次方程组有唯一解 ⇔ \Leftrightarrow ⇔ r ( A ) = n . r(A)=n. r(A)=n.
- 非齐次方程组有无数解 ⇔ \Leftrightarrow ⇔ r ( A ) < n . r(A)<n. r(A)<n.
- 非齐次方程组无解 ⇔ \Leftrightarrow ⇔ r ( A ‾ ) = r ( A ) + 1. r(\overline{A})=r(A)+1. r(A)=r(A)+1.
特别地,如果系数矩阵 A A A 为 n n n 阶方阵,还有以下结论:
- 非齐次方程组有解 ⇔ \Leftrightarrow ⇔ r ( A ‾ ) = r ( A ) . r(\overline{A})=r(A). r(A)=r(A).
- 非齐次方程组有唯一解 ⇔ \Leftrightarrow ⇔ ∣ A ∣ ≠ 0. |A| \ne 0. ∣A∣=0.
- 非齐次方程组有无数解 ⇔ \Leftrightarrow ⇔ ∣ A ∣ = 0. |A|=0. ∣A∣=0.
- 非齐次方程组无解 ⇔ \Leftrightarrow ⇔ r ( A ‾ ) = r ( A ) + 1. r(\overline{A})=r(A)+1. r(A)=r(A)+1.
在学向量时就已经讨论了矩阵、向量和方程组解的关系的话,现在来学就会非常轻松。
对于系数矩阵是方阵的方程组,无非就是将行列式和秩联系了起来。如果矩阵的秩那一部分学得到位,也不是什么难点。因此如果要记忆就记忆秩的关系就好,行列式的结论自然能想到。
三、线性方程组解的结构
- 设 X 1 , X 2 , … , X s \pmb{X_1,X_2,\dots,X_s} X1,X2,…,Xs 为齐次线性方程组 A X = 0 \pmb{AX=0} AX=0 的一组解,则 k 1 X 1 + k 2 X 2 + ⋯ + k s X s k_1X_1+k_2X_2+\dots +k_sX_s k1X1+k2X2+⋯+ksXs 也为齐次线性方程组 A X = 0 \pmb{AX=0} AX=0 的解,其中 k 1 , k 2 , … , k s k_1,k_2,\dots,k_s k1,k2,…,ks 为任意常数。
- 设 η 0 \pmb{\eta_0} η0 为非齐次线性方程组 A X = b \pmb{AX=b} AX=b 的一个解, X 1 , X 2 , … , X s \pmb{X_1,X_2,\dots,X_s} X1,X2,…,Xs 为齐次线性方程组 A X = 0 \pmb{AX=0} AX=0 的一组解,则 k 1 X 1 + k 2 X 2 + ⋯ + k s X s + η 0 k_1X_1+k_2X_2+\dots +k_sX_s+\pmb{\eta_0} k1X1+k2X2+⋯+ksXs+η0 为非齐次线性方程组 A X = b \pmb{AX=b} AX=b 的解。
- 设 η 1 , η 2 \pmb{\eta_1,\eta_2} η1,η2 为非齐次线性方程组 A X = b \pmb{AX=b} AX=b 的两个解,则 η 1 − η 2 \pmb{\eta_1-\eta_2} η1−η2 为齐次线性方程组 A X = 0 \pmb{AX=0} AX=0 的解。
- 设 X 1 , X 2 , … , X s \pmb{X_1,X_2,\dots,X_s} X1,X2,…,Xs 为非齐次线性方程组 A X = b \pmb{AX=b} AX=b 的一组解,若 k 1 X 1 + k 2 X 2 + ⋯ + k s X s k_1X_1+k_2X_2+\dots +k_sX_s k1X1+k2X2+⋯+ksXs 也为非齐次线性方程组 A X = b \pmb{AX=b} AX=b 的解的充要条件是 k 1 + k 2 + ⋯ + k s = 1. k_1+k_2+\dots+k_s=1. k1+k2+⋯+ks=1.
- 设 X 1 , X 2 , … , X s \pmb{X_1,X_2,\dots,X_s} X1,X2,…,Xs 为非齐次线性方程组 A X = b \pmb{AX=b} AX=b 的一组解,若 k 1 X 1 + k 2 X 2 + ⋯ + k s X s k_1X_1+k_2X_2+\dots +k_sX_s k1X1+k2X2+⋯+ksXs 为齐次线性方程组 A X = 0 \pmb{AX=0} AX=0 的解的充要条件是 k 1 + k 2 + ⋯ + k s = 0. k_1+k_2+\dots+k_s=0. k1+k2+⋯+ks=0.
是不是有点熟悉,特别像我们在微分方程中学的关于高阶线性微分方程的解的结构。
- 齐次解线性组合仍为齐次解。
- 齐次解 + 非齐次解为非齐次解。
- 非齐次解相减为齐次解。
- 非齐次解线性组合,系数之和为 1 才是非齐次解。
- 非齐次解线性组合,系数之和为 0 才是齐次解。
写在最后
线性方程组还有些内容,是关于计算的,我们放在后面来细说!