一、最小生成树

性质：

（1）不唯一（2）权值之和是唯一的（3）删去一条边会变成非连通图，增加一条边会产生回路（4）最小生成树的边数为顶点数减一

1、Prim算法

m个顶点，n条边

算法过程：每次选择距离当前集合的最短路径，直至所有的点加入

初始化：向空树加入图中的任意顶点

循环：选择图内距离当前图的最短路径，并加入

时间复杂度：   不依赖于边的数量，适用于边稠密图

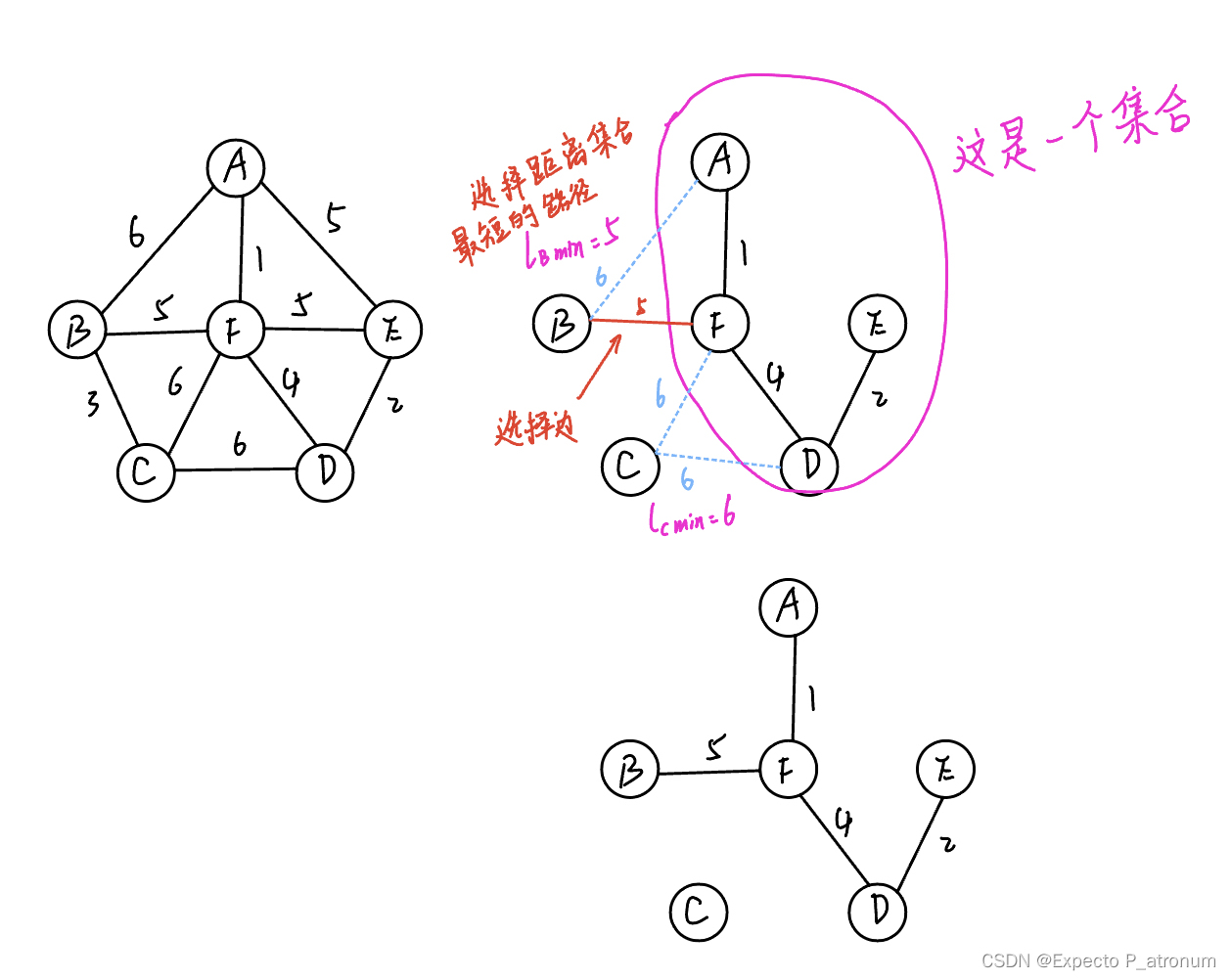
2、Kruskal算法

算法过程：选择距离最短且连通两个不同的联通分量上的边加入空树

时间复杂度：

        使用堆存放边：

        使用并查集：

适用于边稀疏图

二、最短路径

1、Dijkstra算法（贪心）

负权边不适用

算法过程：

1、选择源点，集合S为最短路径集合，V为全部路径集合

2、选择源点距离｜V-S｜的最短路径，更新最短路径集合

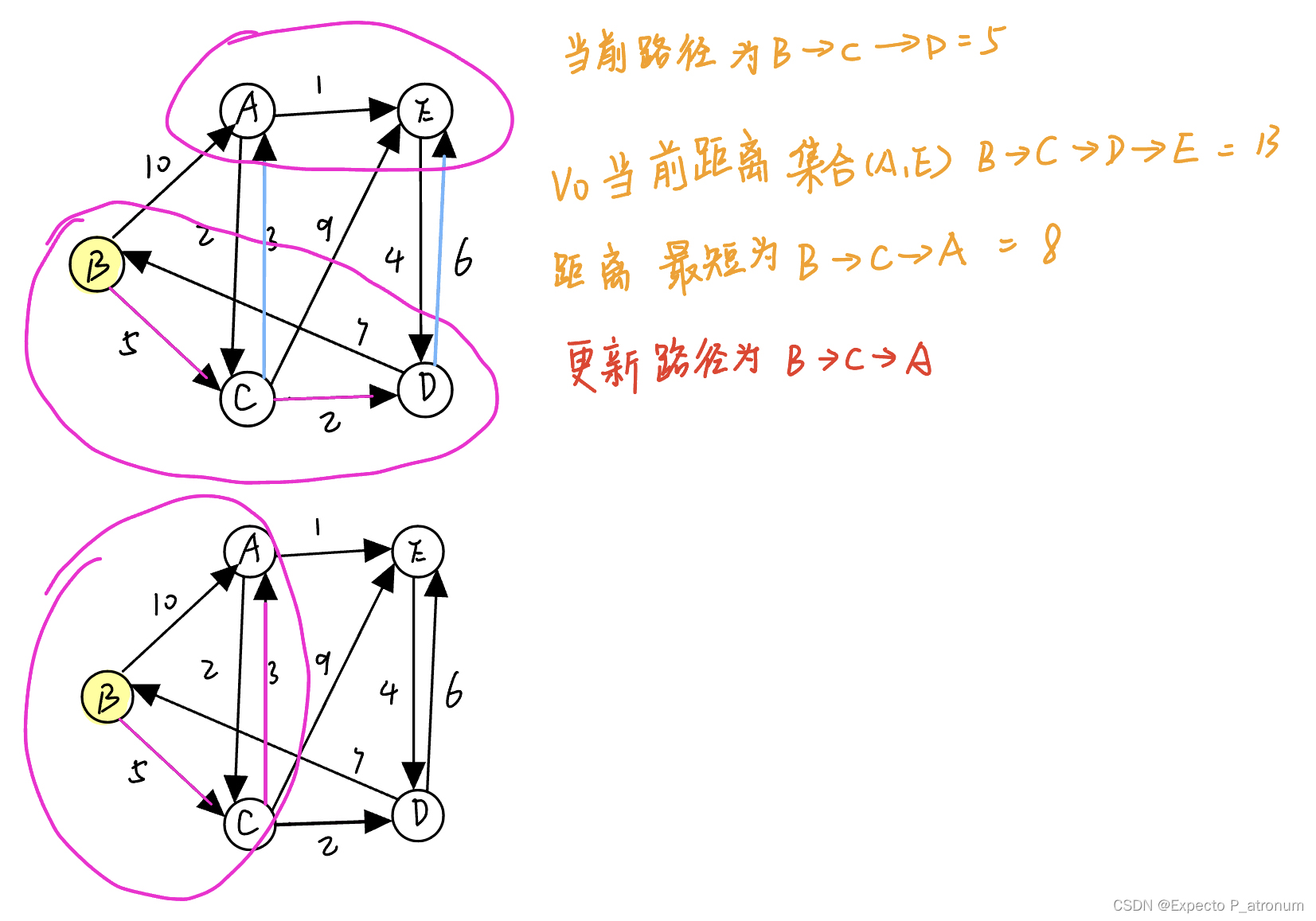
 2、Floyd算法（动态规划）

算法过程：

通过状态转移方程更新矩阵

​​​​​​​

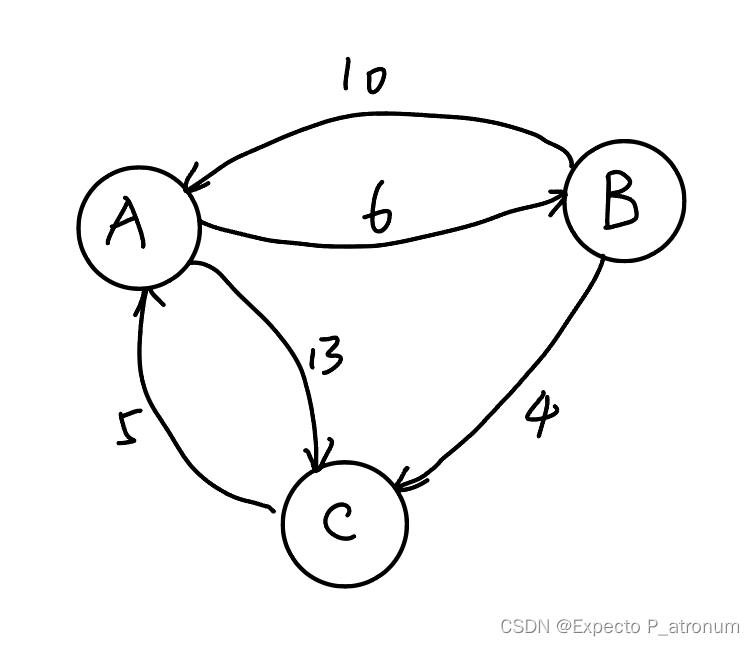
（1）初始：  

（2）以A为中间点，B-A-C=  11 

更新一次后：

……不断更新至

 三、拓扑排序（判断图是否有环）

（1）每个顶点出现且只出现一次

（2）若顶点A在序列中排在顶点B的前面，则在图中不存在从顶点B到顶点A的路径

1、关键路径（考题）

关键活动 ：l(i) - e(i) = 0 

顶点表示事件，有向边表示活动

a.某事件发生后，从该顶点出发的活动才能开始

b.指向某事件的所有活动结束时，该事件才能发生

tips：

1、关键路径不唯一，只有加快所有关键路径上共同的关键活动才能缩短工期

2、不能任意缩短关键路径，可能会导致该路径变为非关键路径

​​​​​​​

（1）事件最早发生时间ve(k)

从vi到vk的最长路径长度，从前往后计算

ve(k) = Max{ve(j)+weight(vj,vk)}

计算步骤：

初始：ve(1) = 0//每道题都一样

比较：当前节点k所有被指向的节点j之间进行比较中的最大值——边的权值加上ve(j)

——ve(2) = ve(1) + 3 = 3 , ve(3) = ve(1) + 2 = 2

——ve(4) = max{ve(2) + 2 , ve(3) + 4} = 6

……

（2）时间最迟发生时间vl(k)

最迟必须发生时间

从后往前计算，逆拓扑排序

vl(k) = Min{vl(j) - Weight(vk,vj)}

计算步骤：

初始：vl(n) = 8

比较：当前节点k所有指向的节点j之间进行比较中的最小值——边的权值加上ve(j)

（3）活动最早开始时间e(k)

        e(i) = ve(k)

        等于第i条边的起点的ve(k)

（4）活动最迟开始时间l(i)

        l(i) = vl(j) - w(vk,vj)  

第i条边的终点的vl(j)减去边的权值