ResNet与Vgg的主要区别:
1.ResNet相较于Vgg具有更加深的网络结构
2.ResNet相较于Vgg引入了残差连接的结构
3.ResNet引入了BatchNorm层,使得ResNet能够训练更加深的网络结构
4.ResNet使用stride=2的卷积层代替了Vgg中池化层进行下采样
5.ResNet相较于Vgg设计的很大的不同点在于ResNet当feature map尺寸下降一半时,卷积层通道数增加一倍
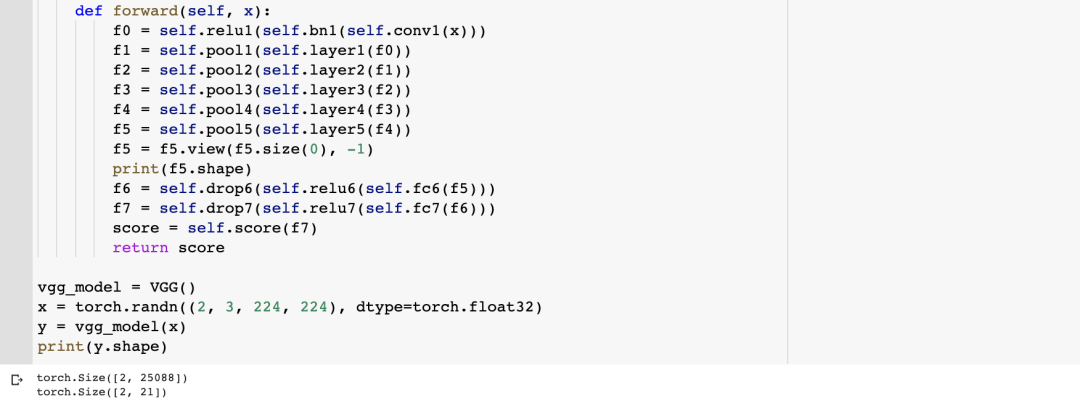
VGG

ResNet 网络是在 2015年 由微软实验室中的何凯明等几位大神提出,斩获当年ImageNet竞赛中分类任务第一名,目标检测第一名。获得COCO数据集中目标检测第一名,图像分割第一名。

ResNet是在VGG的基础上进行改造。引入了skip connect跳层连接避免了梯度消失,梯度爆炸等现象。
一、Skip Connection是什么?
Skip Connection(跳跃连接),是一种在深度神经网络中连接不同层次之间节点的方法。在传统的神经网络中,信号从输入层传输到输出层,每个隐藏层的输出都需要经过激活函数处理后再传输到下一层,而Skip Connection会将当前层的信号同时向后传输到更深层次的下一层,也就是“跳过”了中间的层次。而这种跨层的连接方式,可以加速信息传输、避免梯度消失,并且保留更多的信息。
二、Skip Connection的优点
对于深度神经网络而言,Skip Connection的优点如下:
1、解决梯度消失问题
随着神经网络层数的增加,梯度消失的问题更加严重,导致深层次的节点很难得到有效的更新,甚至训练过程会完全停滞。而Skip Connection可以保留更多的信息,使得梯度可以通过跨层连接在不同的层次之间传播,从而有效地解决梯度消失问题。
2、加速模型训练
由于Skip Connection允许信号直接传输到更深层次的下一层,而不必经过中间的层次,从而可以缩短神经网络的传输路径,加速信息的传输速度以及整个神经网络的训练速度。
3、提高模型的泛化能力
在一些深度神经网络的训练中,由于训练集与测试集的差异,造成了过拟合的现象。通过加入Skip Connection,可以让更多的信息有机会被保留下来,从而增强模型的泛化能力,降低过拟合的风险。
残差网络建立在BN之上,用多项式拟合差值。优点是在解附近权重的反应更加灵敏,能够更容易学习到最优解

ResNet
网络的深度为什么重要?
因为CNN能够提取low/mid/high-level的特征,网络的层数越多,意味着能够提取到不同level的特征越丰富。并且,越深的网络提取的特征越抽象,越具有语义信息。
为什么不能简单地增加网络层数?
对于原来的网络,如果简单地增加深度,会导致梯度弥散或梯度爆炸。
对于该问题的解决方法是正则化初始化和中间的正则化层(Batch Normalization),这样的话可以训练几十层的网络。
虽然通过上述方法能够训练了,但是又会出现另一个问题,就是退化问题,网络层数增加,但是在训练集上的准确率却饱和甚至下降了。这个不能解释为overfitting,因为overfit应该表现为在训练集上表现更好才对。
退化问题说明了深度网络不能很简单地被很好地优化。
作者通过实验:通过浅层网络+ y=x 等同映射构造深层模型,结果深层模型并没有比浅层网络有等同或更低的错误率,推断退化问题可能是因为深层的网络并不是那么好训练,也就是求解器很难去利用多层网络拟合同等函数。
怎么解决退化问题?
深度残差网络。如果深层网络的后面那些层是恒等映射,那么模型就退化为一个浅层网络。那现在要解决的就是学习恒等映射函数了。 但是直接让一些层去拟合一个潜在的恒等映射函数H(x) = x,比较困难,这可能就是深层网络难以训练的原因。但是,如果把网络设计为H(x) = F(x) + x,如下图。我们可以转换为学习一个残差函数F(x) = H(x) - x. 只要F(x)=0,就构成了一个恒等映射H(x) = x. 而且,拟合残差肯定更加容易。
ResNet 模型原理
VGG 网络在特征表示上有极大的优势,但深度网络训练起来非常困难。为了解决这个问题,研究者提出了一系列的训练技巧,如 Dropout、归一化(批量正则化,Batch Normalization)。
2015年,何凯明为了降低网络训练难度,解决梯度消失的问题,提出了残差网络(Residual Network,ResNet)。
图1 梯度消失
ResNet 通过引入跳跃结构(skip connection),让 CNN学习残差映射。残差结构(Bottleneck)如图 2 所示。
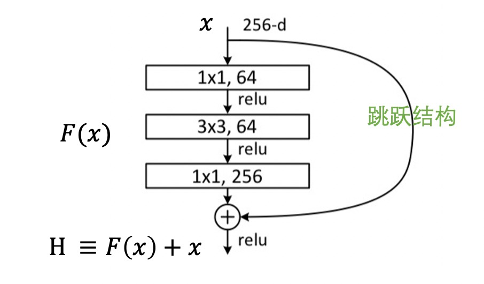
图2 残差结构
图2 的残差结构中,输入 x ,先是 1 x 1 卷积核,64 卷积层,最后是 1 x 1 卷积核,256 卷积层,维度先变小再变大。网络的输出为 H(x),如果没有引入跳跃结构分支, H(x) = F(x),根据链式法则对 x 求导,梯度变得越来越小。引入分支之后,H(x) = F(x) + x,对 x 求导,得到的局部梯度为 1,且当梯度进行反向传播时,梯度也不会消失。
图 3 是 ResNet 的结构,图中展示了 18 层、34 层、50 层、101 层、152 层框架细节,图中 “ x 2” 和 “ x 23 ” 表示该卷积层重复 2 次或 23 次。我们可以发现所有的网络都分成 5 部分,分别是 conv1、conv2_x、conv3_x、conv4_x、conv5_x。
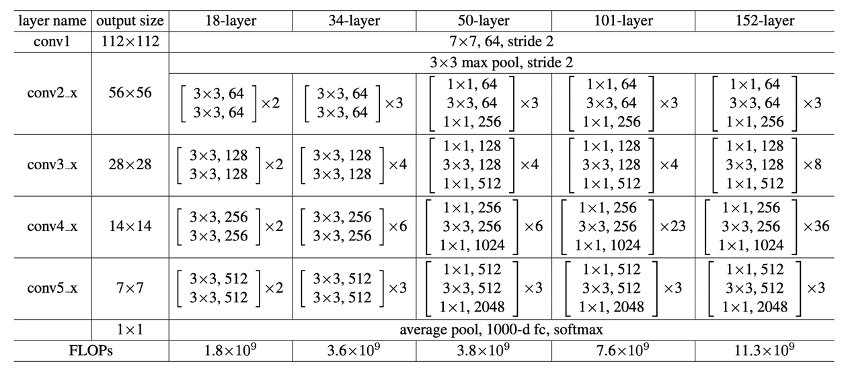
图3 ResNet的结构
图 3 中 conv1 使用的是 7 x 7 的卷积核。当通道数一致时,卷积参数的计算量是 7 x 7 的卷积核 大于 3 x 3 的卷积核 ;当通道数不一致时,若通道数小,则可以采用大的卷积核。
对于第一个卷积层的通道数为 3 时,3个 3 x 3 卷积核与 1 个 7 x 7 卷积核的感受野效果一样,但 1 个 7 x 7 却比 3 个 3 x 3 的参数多。在 VGG 19 层和 ResNet 34 层里,参数的计算量如图 4 所示,ResNet 34 层采用 1 个 7 x 7 的卷积核的计算量远小于 VGG 19 层采用 3 个 3 x 3 的卷积核。

图4 参数的计算量
图 3 中卷积层 conv2_x 和 conv3_x 的输出(output size)的大小分别为56 x 56 和28 x 28,如果卷积层 conv2_x 采用跳跃结构到 conv3_x,由于特征图的维度不一致,不能直接相加,此时的跳跃结构可采用卷积,以保证特征图的维度一致,特征图可以进行相加操作。
图 3 中最后一行的 FLOPs (floating-point operations) 指的是浮点运算次数,可以衡量框架的复杂度。框架的复杂度与权重和偏差(bias)有关。输入图像的高、宽、通道数分别用 H_in、 W_in、D_in 表示;输出的特征图的高、宽、通道数分别用 H_out、 W_out、D_out 表示;卷积核的宽和高分别用 F_w、F_h表示;N_p表示特征图一个点的计算量,其计算公式如下:

一次卷积的 FLOPs 的计算公式如下:
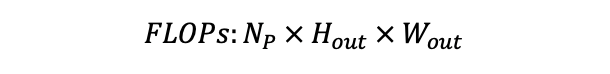
对于全连接层,输入的特征图会拉伸为1 x N_in 的向量,输出的向量维度为 1 x N_out,则一次全连接层的 FLOPs 计算公式如下:

可以使用工具包 Flops 在 PyTorch 中计算网络的复杂度。
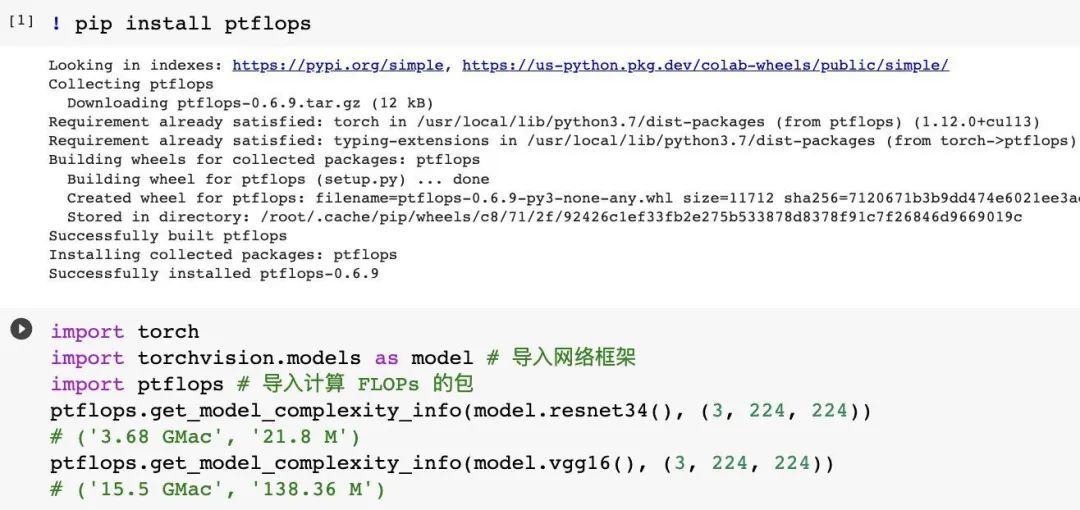
图5 ResNet 34 与 VGG 16 网络的 FLOPs
ResNet 代码复现
ResNet 网络参考了 VGG 19 网络,在其基础上进行了修改,变化主要体现在 ResNet直接使用 stride=2 的卷积做下采样,并且用 Global Average Pool 层替换了全连接层。
ResNet 使用两种残差结构,如下图 5 所示。左图对应的是浅层网络,当输入和输出维度一致时,可以直接将输入加到输出上。右图对应的是深层网络。对于维度不一致时(对应的是维度增加一倍),采用 1 x 1 的卷积,先降维再升维。
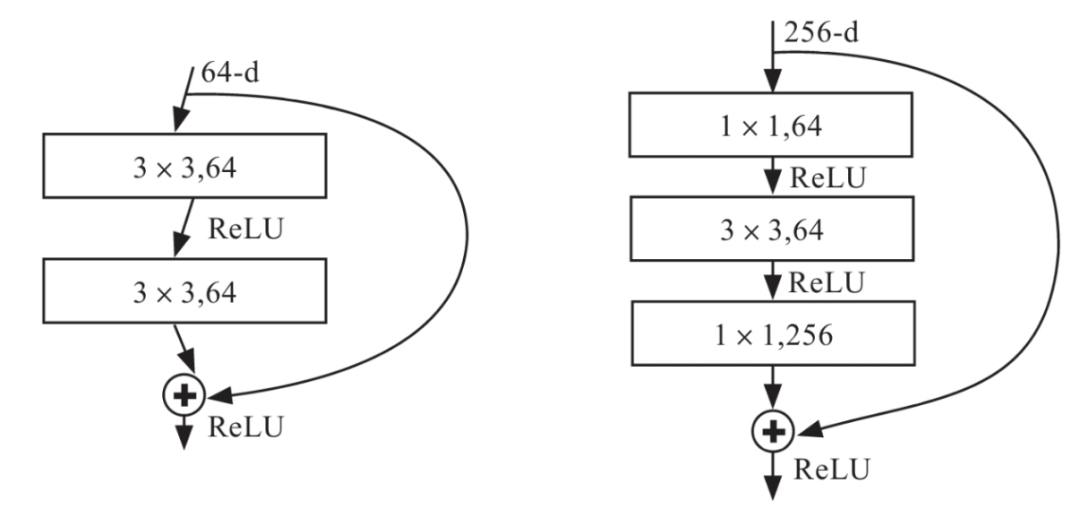
图5 残差结构
两种残差结构的代码实现如下,class BasicBlock(nn.Module) 指的是浅层网络 ResNet 18/34 的残差单元:

class BottleNeck(nn.Module)指的是深层网络 ResNet 50/101/152 的残差单元:

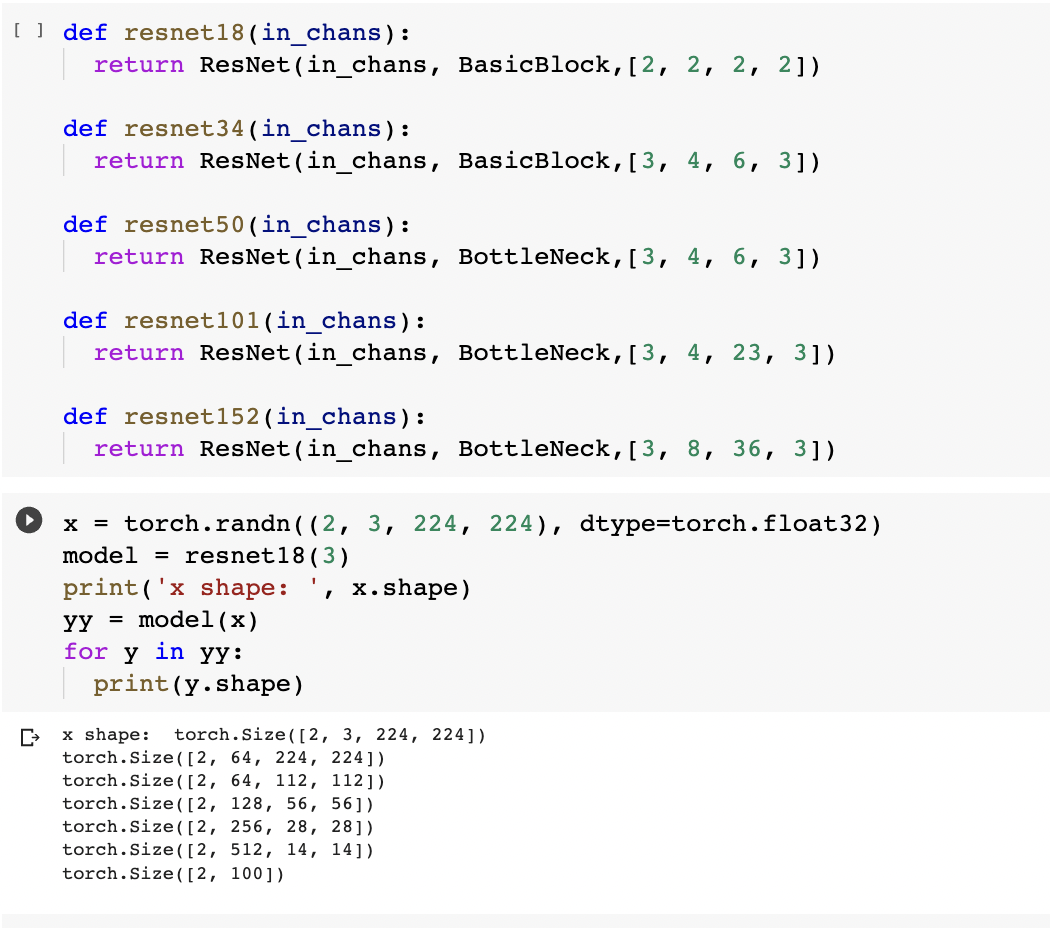
ResNet 的整体结构如下:

在 ResNet 类中的 forward( )函数规定了网络数据的流向:
(1)数据进入网络后先经过卷积(conv1),再进行下采样pool(f1);
(2)然后进入中间卷积部分(conv2_x, conv3_x, conv4_x, conv5_x);
(3)最后数据经过一个平均池化(avgpool)和全连接层(fc)输出得到结果;
中间卷积部分主要是下图中的蓝框部分,红框部分中的 [2, 2, 2, 2] 和 [3, 4, 6, 3] 等则代表了 bolck 的重复次数。
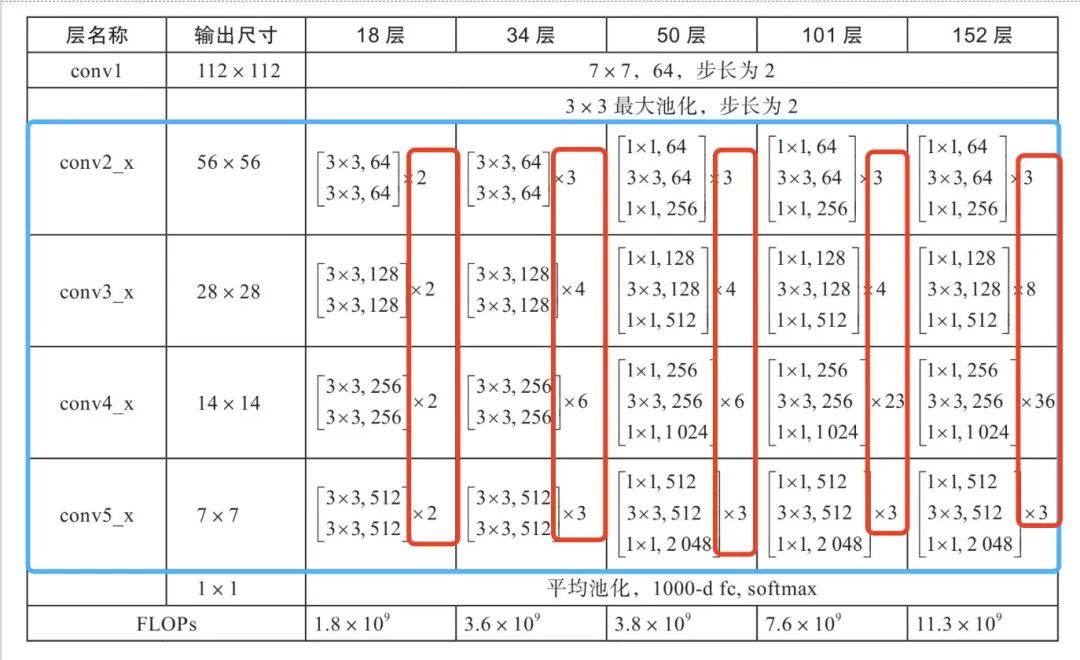
ResNet18和其他Res系列网络的差异主要在于 conv2_x ~conv5_x,其他的部件都是相似的。